Сущность метода ПС заключается в измерении разности естественных электрических потенциалов между электродом М, перемещаемым по скважине, и неподвижным электродом N на поверхности (см. рис. 11.1).
Образование естественных электрических потенциалов в скважинах связано с физико-химическими процессами, протекающими на границе раздела между скважиной и горной породой и внутри горных пород.
По причинам, вызывающим их, потенциалы ПС делятся на: диффузионно-адсорбционные, фильтрационные и окислительно-восстановительные.
Диффузионно-адсорбционные потенциалы
Потенциалы диффузионно-адсорбционной природы возникают вследствие различия в химическом составе и концентрации солей, растворенных в пластовых водах и буровом растворе. На контакте растворов разной концентрации (или состава) происходит диффузия ионов из более концентрированного раствора в менее концентрированный. Однако скорость диффузии неодинакова у разнополярных ионов: у катионов (+) она меньше, у анионов (-) - больше. Вследствие разности в подвижности через некоторое время в более слабом растворе накопится избыток отрицательных ионов, а в концентрированном - положительных, и эти растворы приобретут соответствующий заряд (рис. 10.1).
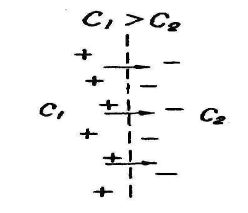
Рис. 10.1. Возникновение диффузионной ЭДС на контакте двух растворов разной концентрации
Разность потенциалов между двумя электролитами разной концентрации подчиняется уравнению В. Нэрнста (1864-1941):
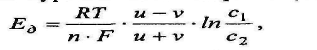(10.1)
Т- абсолютная температура, К; п — валентность ионов в растворе; и - подвижность катионов; v - подвижность анионов; с\,с2 — концентрации контактирующих растворов.
Нетрудно видеть, что при Т = const все параметры, стоящие перед знаком логарифма, дают постоянную величину, называемую коэффициентом диффузионных потенциалов.
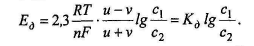(10.2)
Формула Нэрнста справедлива для сильно разбавленных растворов одной и той же соли.
В условиях скважин пластовую воду и буровой раствор можно считать (в первом приближении) растворами NaCl.
Посмотрим, какую величину будет иметь Кд для этой соли. По справочным данным, абсолютная подвижность иона Na+ при 20°С «= 0, 00045 см/с, а иона СГ - v= 0, 00067 см/с.
Если подставить эти значения в выражение Кд, то будем иметь
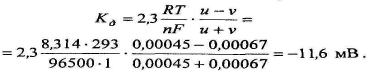(10.3)
Отсюда
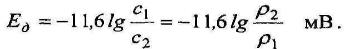(10.4)
Для других солей Ед будет иной, но такого же порядка. С изменением температуры будет меняться и Кд:
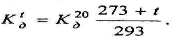(10.5)
Если контакт растворов разной концентрации происходит не непосредственно, а через перегородку (мембрану) из горных пород, то потенциал в этом случае будет отличаться от потенциала Нэрнста из-за того, что мембрана (перегородка) обладает способностью задерживать (сорбировать) определенные ионы. Потенциал в этом случае называется мембранным или диффузионно-адсорбционным - Еда.
Мембранный потенциал также пропорционален логарифму отношения концентраций контактирующих растворов, но коэффициент пропорциональности здесь иной - Кда, зависящий от адсорбционных свойств мембраны и отличающийся от Кд как по величине, так и по знаку.
Для чистых кварцевых песков и песчаников, обладающих нулевой адсорбционной активностью, Кда -Кд =-11,6 мВ (при *=20 °С),.для тонкодисперсных глин, имеющих максимальную адсорбционную активность, Кда = К™™ = +58 мВ. У глинистых песчаников, алевролитов и др. пород Кда имеет промежуточное значение.
Наибольшей величины диффузионно-адсорбционные потенциалы достигают на границе пород с минимальной и максимальной адсорбционной активностью, т.е. на границе чистых кварцевых песчаников и тонкодисперсных глин:
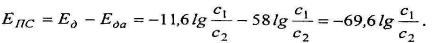(10.6)
Рассмотрим такой пример для условий скважины, когда наблюдается типичное соотношение между минерализацией бурового раствора с0 и пластовых вод св - с0 <св (рис. 10.2).
Песчаный пласт не оказывает влияния на процесс диффузии и на движение ионов. Против песчаного пласта менее концентрированный буровой раствор заряжается отрицательно, песчаник, насыщенный соленой пластовой водой, - положительно. Далее, вместо того, чтобы учитывать 2 других контакта (песчаник - глина и глина - буровой раствор) будем считать, что имеет место контакт пластовой воды с буровым раствором через глину, которая играет роль мембраны. Поскольку глина не пропускает анионы (-) и пропускает катионы (+), то очень скоро раствор меньшей концентрации заряжается положительно по отношению к более концентрированному. Таким образом, раствор в скважине против глин приобретает положительный заряд, против песчаников - отрицательный. Такое распределение знаков ПС, наблюдающееся при условии с0 <св, носит название "прямого поля" ПС.
При обратном соотношении с0 > св имеет место "обратное поле" ПС, когда глины в скважине выделяются положительными, а песчаники -отрицательными потенциалами.
Обратное поле ПС встречается довольно редко потому, что пластовые воды нефтяных месторождений, залегающих на довольно большой глубине, где температура повышена, как правило, имеют и повышенную минерализацию; буровой же раствор приготавливают на основе воды из поверхностных источников (озер, рек) и его минерализация невелика с0 <св. Обратное поле ПС может иметь место при бурении скважин в засушливых районах, когда для приготовления бурового раствора приходится использовать солоноватую воду местных источников, а подземная вода - пресная (со>сд).
Если изолировать при помощи перегородок из непроводящего материала участок столба бурового раствора против пласта-коллектора так, как это показано на рис. 10.2, б, то между пластом и вмещающими его глинами будет зарегистрировано "статическое" значение потенциала собственной поляризации Епс, график которого приведен рядом.
В реальных условиях таких перегородок нет, и всегда существует циркуляция токов ПС \пс в скважине, замыкающихся через сопротивление самой скважины Rc, пласта Япл и вмещающих пород RBM (рис. 10.3). По этой причине наблюденная амплитуда AUпс составляет лишь часть "статической" и равна падению напряжения на участке цепи, образованном скважиной - Rc.
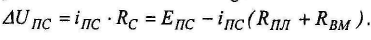(10.7)
Т.к. сечение проводника Rc много меньше, чем сечения в пласте и вмещающих породах, то Rc>Rnn и rc>rbm-
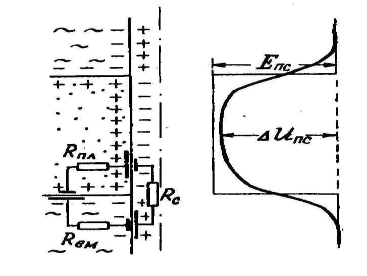
Рис. 10.3. Схема, поясняющая отличие измеряемой разности потенциалов {AU ПС) от
статической амплитуды ПС {Епс)
Если мощность пластов песчаников и глин очень велика, то сечение проводников Rnjj и RBM неограниченно, и при й->а>, Rnjl^> 0 и RBM-* 0; поэтому AUпс я Епс. Если мощность пласта невелика, вблизи второй границы пласта также протекает ток inc, и сечение проводника Rm будет ограничено лишь половиной мощности пласта, и падением напряжения на участке пласт - вмещающие породы уже нельзя будет пренебречь, особенно, если пласт имеет высокое сопротивление. Следовательно, для пластов ограниченной мощности
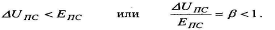(10.8)
Р называется коэффициентом снижения амплитуды или коэффициентом учета мощности.
Задача о распределении потенциала AUnc по оси скважины решена теоретически и на сеточных моделях. Рассчитаны теоретические кривые ПС и номограммы для определения β. Такая номограмма приведена на рис. 10.4.
Наличие зоны проникновения бурового раствора уменьшает амплитуду наблюденной AUnct т.к. в какой-то мере эквивалентно увеличению диаметра скважины d и уменьшению отношения h/d.
Изменение аномалии ПС, связанное с расширением зоны проникновения, показано на рис. 10.5.
По результатам интерпретации диффузионно-адсорбционных ПС можно не только определить границы пластов с различными диффузионно-адсорбционными свойствами, но и определять сопротивление и минерализацию пластовых вод - а это важная задача для нефтяной и даже рудной геологии.
Фильтрационные потенциалы
Фильтрационные потенциалы или потенциалы течения наблюдаются при фильтрации бурового раствора из скважины в пласт или, наоборот, пластовых вод из пласта в скважину (в зависимости от соотношения давлений в пласте и скважине).
Потенциалы течения возникают в связи с адсорбцией ионов поверхностью частиц, слагающих горную породу. Вследствие преобладающей адсорбции ионов одного знака в направлении движения жидкости образуется недостаток этих ионов, и на концах канала (капилляра) возникает разность потенциалов (рис. 10.6).
Математическое обоснование теории фильтрационных потенциалов было дано Г. Гельмгольцем (1821-1894), поэтому потенциалы течения называются еще и потенциалами Гельмгольца. По Гельмгольцу:
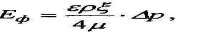(10.9)
где ∆р - перепад давлений;
µ - вязкость раствора;
ε - диэлектрическая проницаемость;
ρ - УЭС раствора;
f - электрокинетический или ξ-потенциал.
ξ -потенциал представляет собой разность потенциалов между неподвижной частью диффузного слоя ионов в капилляре и свободным раствором (рис. 10.7), ξ -потенциал может быть как положительным, так и отрицательным.
Формула (10.9) справедлива для пористой среды, средний эффективный радиус капилляров которой существенно превышает толщину двойного электрического слоя у стенки капилляра.
Знак фильтрационной разности потенциалов определяется знаком ξ - потенциала и направлением фильтрации.
Наблюдения, проведенные в реальных скважинах, показывают, что потенциалы течения неточно подчиняются формуле (10.9). При прочих равных условиях Еф оказываются зависящими еще от проницаемости пород, т.е. от формы и размеров капилляров, по которым фильтруется раствор.
Профессор В.Н. Дахнов считает, что различие между практическими и теоретическими значениями Еф связано с наличием застойной жидкости во впадинах (расширениях) капилляров, из-за чего проводящее сечение электрического тока больше, чем сечение фильтрующейся жидкости.
Фильтрационные потенциалы в скважинах невелики и составляют обычно 4-5, реже 10 мВ. Для сравнения - фильтрационные потенциалы, наблюдаемые в полевой электроразведке, достигают иногда нескольких В.
Несмотря на небольшую величину, фильтрационные потенциалы могут быть использованы на практике для определения пластовых давлений.
В формуле (10.9) все параметры, стоящие перед Ар, являются величинами постоянными, а
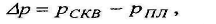
Где, Рскв' гидростатическое давление в скважине, которое легко может
быть вычислено по высоте столба жидкости над пластом; рпл - давление в пласте. Таким образом,
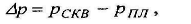(10.11)
Измерив разность фильтрационных потенциалов в скважине, меняют гидростатическое давление, откачав или, наоборот, долив какое-то количество раствора. Снова измеряют фильтрационный потенциал
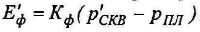(10.12)
Уравнения (10.11) и (10.12) образуют систему с двумя неизвестными Кф и рпл, которую несложно решить и определить рпл.
