Сгруппируем скобки по две так, чтобы сумма свободных членов была одинаковой.
2. Перемножим их.
3. Введем замену переменной.
В нашем уравнении сруппируем первую скобку с третьей, а вторую с четвертой,так как (-1)+(-4)=(-7)+2:
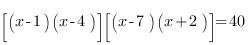
В этом месте замена переменной становится очевидной: 
Получаем уравнение 
Ответ: 
2. 
Уравнение этого типа похоже на предыдущее с одним отличием: в правой части уравнения стоит произведение числа на 
. И решается оно совсем по-другому:
Группируем скобки по две так, чтобы произведение свободных членов было одинаковым.
2. Перемножаем каждую пару скобок.
3. Из каждого множителя выносим за скобку х.
4. Делим обе части уравнения на .
5. Вводим замену переменной.
В этом уравнении сгруппируем первую скобку с четвертой, а вторую с третьей, так как 
:
Заметим, что в каждой скобке коэффициент при и свободный член одинаковые. Вынесем из каждой скобки множитель 
:
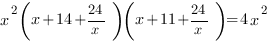
Так как х=0 не является корнем исходного уравнения, разделим обе части уравнения на 
. Получим:
Теперь можем ввести замену переменной: 
Получим уравнение: 
Ответ: 
3. 
Заметим, что в знаменателях обоих дробей стоят квадратные трехчлены, у которых старший коэффициент и свободный член одинаковые. Вынесем, как и в уравнении второго типа х за скобку. Получим:
Разделим числитель и знаменатель каждой дроби на х:
Теперь можем ввести замену переменной:
Получим уравнение относительно переменной t:
Ответ: 
4. 
Заметим, что коэффициенты уравнения симметричны относительно центрального. Такое уравнение называется возвратным.
Чтобы его решить,
1. Разделим обе части уравнения на (Мы можем это сделать, так как х=0 не является корнем уравнения.) Получим:
2. Сгруппируем слагаемые таким образом:
3. В каждой группе вынесем за скобку общий множитель:
4. Введем замену: 
5. Выразим через t выражение 
:
Отсюда 
Получим уравнение относительно t:
Ответ: 
