ЛАБОРАТОРНАЯ РАБОТА
Цель работы: ознакомление с дифракционными картинами различных типов; определение ширины прямоугольной щели при изучении явления дифракции в монохроматическом свете; определение длин волн красного и фиолетового света.
Приборы и принадлежности: дифракционная решетка, экран со щелью, линейка с делениями, осветитель, штатив; установка РМС – 3.
Теоретические сведения
Явление дифракции состоит в отклонении света от прямолинейного распространения в среде с резкими неоднородностями в виде краев непрозрачных и прозрачных тел, узких отверстий, выступов и т.д., в результате чего свет проникает в область геометрической тени, и происходит интерференционное перераспределение интенсивности света. Под дифракцией следует понимать любое отклонение от прямолинейного распространения лучей, если только оно не является следствием обычных законов геометрической оптики – отражения и преломления. Явление дифракции объясняется волновыми свойствами света с использованием принципа Гюйгенса-Френеля.
Основные положения этого принципа:
1. Каждый элемент волновой поверхности, которой достигла в данный момент световая волна, служит источником вторичных волн, амплитуда которых пропорциональна площади элемента.
2. Вторичные волны, созданные элементами одной и той же поверхности, когерентны и при наложении могут интерферировать.
3. Излучение максимально в направлении внешней нормали к элементу поверхности. Амплитуда сферической волны убывает с расстоянием от источника. Излучают только открытые участки волновой поверхности.
Этот принцип дает возможность утверждать отступления от прямолинейного распространения в случае любой преграды. Рассмотрим случай падения плоской волны (параллельного пучка света) на преграду в виде отверстия MN в непрозрачной пластине (рис.1).
Рис. 1
| В соответствии с принципом Гюйгенса-Френеля каждую точку в плоскости отверстия MN можно рассматривать как самостоятельный источник света, испускающий элементарную сферическую волну. Поверхность П1, образованная элементарными волнами, определяет волновой фронт в момент времени t1. Эта поверхность П1 также становится источником вторичных элементарных сферических волн. Кривая, огибающая эти |
элементарные волны в момент времени t2, определяет волновой фронт с поверхностью П2.
Из рис. 1 видно, что световые лучи, будучи перпендикулярны волновому фронту, отклоняются от своего первоначального направления и попадают в область геометрической тени.
Решить задачу о дифракции света – значит исследовать вопросы, относящиеся к интенсивности результирующей световой волны в различных направлениях. Основным вопросом при этом исследовании является изучение интерференции света, при которой налагающиеся волны могут не только усиливаться, но и ослабляться. Одним из важных случаев дифракции является дифракция в параллельных лучах. Она используется при рассмотрении действия оптических приборов (дифракционная решетка, оптические инструменты, и т. д.). Дифракционная решетка в простейшем случае представляет собой стеклянную прозрачную пластинку, на которой нанесены штрихи равной ширины на одинаковом расстоянии друг от друга. Такая решетка может быть использована в спектральной установке обычного типа вместо призмы как диспергирующая система. Чтобы легче было разобраться в довольно сложном физическом явлении интерференции дифрагированных пучков света на N щелях решетки, рассмотрим вначале дифракцию на одной, затем на двух щелях и, наконец, запишем выражение для N щелей. Чтобы упростить расчёт, используем метод зон Френеля.
Дифракция на одной щели. Рассмотрим дифракцию в параллельных лучах на одной щели. Тип дифракции, при котором рассматривается дифракционная картина, образованная параллельными лучами, получил название дифракции в параллельных лучах, или дифракции Фраунгофера. Щель представляет собой прямоугольное отверстие в непрозрачной пластине, причем одна из сторон намного больше другой. Меньшая сторона называется шириной щели а. Такая щель является препятствием для световых волн, и на ней можно наблюдать дифракцию. В лабораторных условиях дифракция на щели отчетливо наблюдается, если ширина щели а сравнима по величине с длиной световой волны. Пусть монохроматическая световая волна падает нормально к плоскости щели шириной a (расстояние АВ). За щелью установлены собирающая линза и экран, помещённый в фокальной плоскости линзы. Схема представлена на рис. 2.
Рис. 2
Согласно принципу Гюйгенса, каждая точка фронта волны, дошедшей до щели, является новым источником колебаний, причём фазы этих волн одинаковы, так как при нормальном падении света плоскость щели совпадает с плоскостью волнового фронта. Рассмотрим лучи монохроматического света от точек, лежащих на фронте АВ, направление распространения которых составляет угол 
с нормалью. Опустим из точки А перпендикуляр АС на направление луча, распространяющегося из точки В. Тогда, распространяясь дальше от АС, лучи не изменят разность хода. Разностью хода лучей является отрезок ВС. Для расчёта интерференции этих лучей применим метод зон Френеля.
Разделим отрезок ВС на отрезки длиной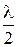 
. На ВС уложится z таких трезков:
z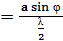 
, (1)
где 
.
Проведя из концов этих отрезков линии, параллельные АС, до встречи с АВ, разобьем фронт волны в щели на ряд полосок одинаковой ширины, количество которых равно z. Они и являются зонами Френеля, так как соответствующие точки этих полосок являются источниками волн, дошедших до точки наблюдения М по данному направлению с взаимной разностью хода 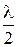. Амплитуды волн от полосок будут одинаковы, потому что фронт плоский и площади их равны. Согласно теории зон Френеля, лучи от двух соседних зон гасят друг друга, так как фазы их противоположны. Тогда при чётном числе зон Френеля (z=2m, где m – целое число, m=1,2,3...), укладывающихся в щели, в точке М будет минимум дифракции, а при нечётном (z=(2m+1)) – максимум. Уравнение (1) тогда запишем следующим образом:
,
.
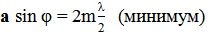Распределение интенсивности в дифракционной картине от одной щели показано на рис. 3. По оси абсцисс отложено расстояние от нулевого максимума вдоль экрана, на котором располагается спектральная картина.
Рис. 3
Дифракция на двух щелях. Для увеличения интенсивности и более чёткого разделения цветов пользуются не одной щелью, а дифракционной решёткой, которая представляет собой ряд параллельных щелей одинаковой ширины a, разделенных между собой непрозрачными промежутками шириной b. Сумма a+b=d называется периодом или постоянной дифракционной решетки.
Для того чтобы найти распределение освещенности на экране в случае решетки, необходимо учесть не только интерференцию волн, вышедших из каждой отдельной щели, но и взаимную интерференцию волн, пришедших в данную точку экрана из соседних щелей. Допустим, что имеется всего две щели. Монохроматическая волна падает нормально к плоскости щелей. Когда в щели укладывается четное число зон Френеля, выполняется условие минимума для щели. Поскольку для каждой щели выполняется условие минимума, то и для всей решетки тоже. Следовательно, условие минимума, для решетки совпадает с условием минимума для щели, оно называется условием главного минимума, и имеет вид
.
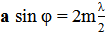Рассмотрим случай, когда в щели укладывается нечетное число зон Френеля. При этом в каждой щели останется по одной нескомпенсированной зоне Френеля, в которой все источники света колеблются в одной фазе. Эти нескомпенсированные лучи, прошедшие через одну из щелей, будут интерферировать с нескомпенсированными лучами, прошедшими через другую щель. Выберем два произвольно направленных луча (рис. 4), исходящих из соответствующих точек соседних щелей и падающих в одну точку на экране. Их интерференцию определяет разность хода BC= d sin . Если BC= 
, то в точке М свет усилен. Уравнение
, (m=1,2,3…)
определяет главные максимумы. Если,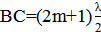 
, то в точке М свет ослаблен. Уравнение
является условием добавочных минимумов, появившихся вследствие наличия второй щели.
Рис. 4
Если b > a, то ширина основной части дифракционной картины от двух щелей остаётся прежней. Большая часть энергии сосредоточена в пределах центрального максимума. Пунктиром показано распределение интенсивности для одной щели. Если b < a дифракционная картина будет несколько сужена. При b =0 получаются пики, которые в 2 раза уже, так как имеется не две щели шириной a, а одна щель шириной 2 a.
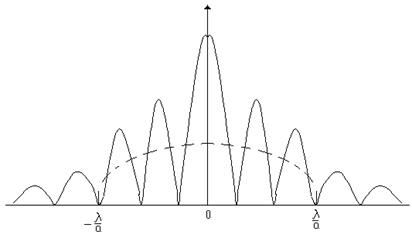
Рис. 5
Дифракция на N щелях. Расчет дифракционной картины на дифракционной решетке довольно сложен с математической точки зрения, но в принципе ничем не отличается от рассмотрения дифракции на двух щелях. Следует учесть, что в случае дифракции на двух щелях появляется некоторое число дополнительных максимумов и минимумов. При наличии третьей щели, их число возрастает, так как необходимо учесть вклад в дифракционную картину от каждой щели. По мере роста числа щелей на дифракционной решетке растет число дополнительных максимумов и минимумов. Условие главных максимумов и минимумов для дифракционной решетки остаётся тем же самым, что и для двух щелей
, m=0,1,2… (главные максимумы), (2)
, m=1,2,3… (главные минимумы), (3)
а дополнительные минимумы определяются условием:
, m=0,1,2… (4)
Если дифракционная решетка состоит из N щелей, то условием главных максимумов является условие (2), а главных минимумов условие (3).
Условие дополнительных минимумов:
, (5)
где N - общее число щелей решетки (m¢=1, 2,…, N-1, N+1,…, 2N-1, 2N+1,…). В формуле (5) m¢ принимает все целочисленные значения, кроме 0, N, 2N,, т. е. кроме тех, при которых условие (5) переходит в (2).
Сравнивая формулы (2) и (5), видим, что число главных максимумов в N раз меньше общего числа дополнительных минимумов. Действительно, число (или порядок) дополнительных минимумов, отвечающих углу , получается из формулы (2) следующим:
,
а общее число дополнительных минимумов, как видно из формулы (5),
,
откуда следует 
.
Таким образом, между двумя главными максимумами находится (N-1) дополнительных минимумов, разделенных побочными максимумами. Вклад этих побочных максимумов в общую дифракционную картину невелик, так как интенсивность их мала и быстро убывает по мере удаления от главного максимума данного порядка. Поскольку с увеличением числа штрихов решетки все большее количество световой энергии проходит через нее и одновременно происходит увеличение числа дополнительных максимумов и минимумов. Это означает, что главные максимумы становятся более узкими и яркость их возрастает, то есть возрастает разрешающая способность решетки.
Если на решетку падает свет, содержащий ряд спектральных компонентов, то в соответствии с формулой (2), главные максимумы для разных компонентов образуются под разными углами. Таким образом, решетка разлагает свет в спектр.
Характеристиками решетки как спектрального прибора является угловая дисперсия и разрешающая способность.
Угловой дисперсией называется величина 
, где 
- угловое расстояние между двумя спектральными линиями, отличающимися по длине волны на 
. Дифференцируя формулу (2), получим:
.
Разрешающей способностью называется величина 
, где - наименьшая разность длин волн двух спектральных линий, которые видны в спектре раздельно.
Согласно критерию Релея две близкие линии считают разрешенными (видны раздельно), в том случае, если интенсивность в промежутке между ними составляет не более 80% от интенсивности максимума, т.е. I=0,8I0, где I0 – интенсивность главного максимума, I – интенсивность промежутка между двумя соседними максимумами (рис. 6).
Из условия Релея следует:
,
т.е. разрешающая способность решетки растет с увеличением числа щелей N и зависит от порядка спектра.
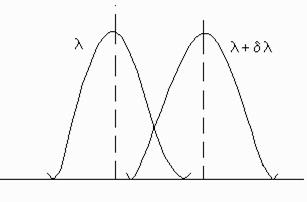
Рис. 6
ЗАДАНИЕ 1. Определение длин волн красного и фиолетового света
Описание лабораторной установки
Экспериментальная установка состоит из штатива, на котором закреплена горизонтально расположенная линейка с делениями, дифракционная решетка, экран со щелью (для получения узкого пучка света) и осветитель. Используемая в работе дифракционная решетка имеет на 1 мм 100 штрихов, т.е. период решетки d =0,01 мм. Луч света, проходя через узкую щель, а затем дифракционную решетку, попадает на хрусталик глаза, который играет роль двояковыпуклой линзы. В дальнейшем распространении изображение спектров и шкалы с делениями на экране со щелью доходит до сетчатки глаза. Таким образом мы видим изображение спектров на шкале.
Из условия максимума m-го порядка для дифракционной решетки выражается длина волны:
где d – период дифракционной решетки, sin φ – синус угла, при котором наблюдается данная линия в спектре, m – порядок спектра, в котором наблюдается линия.
Углы φm, под которыми наблюдаются линии в спектрах, являются малыми, поэтому sin φm ≈ tg φm. Используя это условие, получим:
. (6)
Формула (6) является рабочей для определения длины волны наблюдаемой линии в спектре m-го порядка.
Порядок выполнения работы
1. Включить осветитель.
2. Установить экран со щелью на расстояние L от дифракционной решетки.
3. Приблизить глаз к решетке на удобное расстояние (по обе стороны от щели на черном фоне шкалы должны быть видны дифракционные спектры). При этом глаз должен находиться на близком расстоянии от решетки (рис. 7).
Рис. 7
4. По шкале экрана определить положение красных и фиолетовых линий S в спектрах 1-го и 2-го порядка, расположенных справа и слева от щели для различных расстояний L (L=15 см, 20 см, 25 см). Результаты измерений занести в Таблицу 1.
Таблица 1
| № | Порядок спектра m | S | L | d | λК | λФ | ΔλК | ΔλФ | ||
| Справа | Слева | Среднее | ||||||||
| . . . |
5. Вычислить tgφ по формуле
.
6. По формуле (6) вычислить длины волн красного и фиолетового света для спектров различных порядков и для разных расстояний L.
7. Вычислить среднее арифметическое значение длины волны для красного и фиолетового света по формуле:
, где n – число измерений.
8. Вычислить оценку средней квадратичной ошибки по формуле:
.
9. Вычислить границу случайной погрешности по формуле:
,
где tα(n) – коэффициент Стьюдента, α=0,95, t 0,95 (6)=2,6.
10. Записать окончательный результат в виде:
λ= 
±Δλ, нм; α=0,95.
Контрольные вопросы
1. Какие волны называются когерентными?
2. В чем заключаются явления интерференции и дифракции света?
3. Что называют волновым фронтом, волновой поверхностью?
4. В чем заключается метод зон Френеля?
5. Сформулируйте принцип Гюйгенса – Френеля.
6. Нарисуйте и объясните дифракционные картины, получаемые от одной щели и от дифракционной решетки при освещении их монохроматическим и белым светом.
7. Объясните возникновение главного максимума, главного минимума и дополнительного минимума при дифракции на решетке. Записать их формулы.
8. Как изменится вид дифракционной картины от решетки, если источник света заменить монохроматическим?
9. Расскажите о применении дифракции в науке и технике.
