В термодинамически неравновесных системах, т.е. в системах, для которых значения макропараметров (Т, р,) в разных ее точках различны, возникают необратимые процессы, получившие название явлений переноса. В результате таких процессов из одной локальной области системы в другую происходит перенос энергии (явление теплопроводности), массы (явление диффузии), импульса (внутреннее трение), заряда и т.д. Это ведет к выравниванию значений макропараметров по объему системы. Понятно, что перенос любой величины объясняется переходом с места на место некоторого числа частиц (молекул и атомов) в результате их хаотического движения.
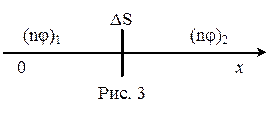Получим общее уравнение переноса вдоль произвольного направления. Направим вдоль него ось О х (рис 3). Выделим мысленно элемент плоскости площадью ∆S, перпендикулярный О х. В силу хаотичности движения за время ∆t через ∆S в направлении О х переместится N частиц:
(1)
Здесь n – концентрация молекул (атомов), а 
– их средняя арифметическая скорость. Переходя через ∆S, каждая молекула переносит присущие ей массу, заряд, импульс, энергию или какие-то другие свои характеристики. Обозначим значение величины, переносимое одной молекулой буквой φ. Тогда за время ∆t через площадку ∆S в направлении оси О х будет перенесено количество физической величины
(2).
Очевидно, если концентрация справа тоже n, то и справа налево перейдет столько же частиц. Т.е. результирующий перенос в этом случае равен нулю: ΔN = 0 и ΔNφ = 0.
Если же среда неоднородна, т.е. либо концентрация частиц, либо значения φ для частиц слева и справа неодинаковы, то более вероятными будут переходы из областей, где значение (nφ) больше в области, где оно меньше. Если предположить, что (nφ)1 > (nφ)2, то результирующий перенос величины φ будет определяться соотношением: 
. (3)
Знак «минус» в (3) отражает факт убыли величины (nφ) в направлении переноса.
Выясним, на каком расстоянии от ∆S слева и справа следует взять значения (nφ). Т.к. изменение физических характеристик молекул происходит только при соударениях, а до соударения каждая из молекул прошла расстояние равное длине свободного пробега, то можно считать, что (nφ) молекул сохраняются неизменными на расстоянии, равном длине свободного пробега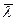 
влево и вправо от ∆S. Разделим и умножим правую часть (3) на 2 :
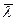(4)
Распределение величин вдоль какого-либо направления определяется характеристикой, которая называется – градиент. Градиент это изменение величины на расстоянии равном единице длины.
В данном случае, в точке с координатой х 2 значение перенасимой величины – (nφ)2, а в точке х 1 – (nφ)1, тогда под градиентом величины nφ, переносимой вдоль оси О х, следует понимать отношение:
.
Тогда 
градиент величины nφ в области ∆S.
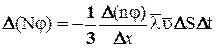. (5)
(5) – общее уравнение переноса.
Диффузия – это перенос массы вещества. При условии, что массы молекул одинаковы (m0 = const), температура газа по объёму одинакова (T = const) и однородного по объему распределения скоростей ( = const), подставляя вместо φ массу молекулы в (5), получим:
, или 
. (6)
Это закон Фика. D =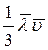 
– коэффициент диффузии. [D] = м2/с.
Теплопроводность – это перенос энергии. При условии, что по всему объему газа концентрация молекул (n = const), массы молекул одинаковы (m0 = const), распределение скоростей по объёму однородно ( = const), а средняя кинетическая энергия поступательного движения одной молекулы 
, получим закон Фурье:
, или 
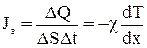. (7)
– коэффициент теплопроводности. [χ] = Вт/(м·К) = кг·м/(с3·К).
Вязкость – это перенос импульса между параллельными слоями, которые упорядоченно движутся со скоростями u1 и u2. При условии, что по всему объему газа концентрация молекул n = const, массы молекул одинакова (m0 = const), распределение скоростей по объёму однородно ( = const), а модуль импульса одной молекулы, связанный со скоростью упорядоченного движения слоев φ = р = m0u, для импульса силы взаимодействия слоёв имеем:
, или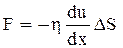 
. ()
Это уравнение Ньютона, которое определяет величину силы внутреннего трения (вязкости). 
– поперечный градиент скорости, характеризующий быстроту изменения скорости в направлении х перпендикулярном движению трущихся слоев. η – динамический коэффициент вязкости 
. [η] = Па·с.
