"Криволинейные интегралы"(12.05.12)
Задача 1. Плоская материальная кривая Гс линейной плотностью
μ = μ (x, y) задана параметрическими уравнениями. Найти
массу Мг дуги кривой:
1). Г: x = 3 (t – sin t), y = 3 (1 – cos t)(t є [ 0, 2π ]); μ = 
;
2). Г: x = 5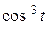 
, y = 5 
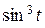(t є [- 
, ]); μ = | y |;
3). Г: x = cos t + t sin t, y = sin t – t cos t (t є [ 0, 2π ]); μ =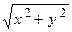 
;
4). Г: x = (
– 2) sin t + 2 t cos t, y = (2 – ) cos t + 2 t sin t,
(t є [ 0, π ]); μ = 
;
5). Г: x =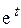 
(cos t + sin t), y = 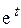(cos t – sin t) (t є [ 0, 
]);
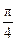μ =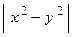 
;
6). Г: x = 2 cos t – cos 2 t, y = 2 sin t – sin 2 t (t є [ 0, 2π ]); μ = ;
7). Г: x = 4 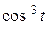, y = 4 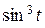(t є [ , 
]); μ = | x y |;
8). Г: x = 2 (t – sin t), y = 2 (1 – cos t)(t є [ 0, 2π ]); μ = y;
9). Г: x = 2 (cos t + t sin t), y = 2 (sin t – t cos t) (t є [- , ]);
μ = ;
10). Г: x = 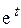(cos t + sin t), y = 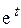(cos t – sin t) (t є [ 0, π ]); μ = | x y |;
11). Г: x = 2 t cos t, y =2 t sin t (t є [ 0, 1 ]); μ = 2 ;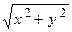
12). Г: x = 5 (t – sin t), y =5 (1 – cos t) (t є [ 0, ]); μ =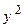 
;
13). Г: x = 2 (cos t + t sin t), y = 2 (sin t - t cos t) (t є [ 0, 2π ]); μ = ;
14). Г: x = 2 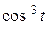, y = 2 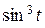(t є [- , ]); μ =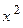 
;
15). Г: x = 4 (t - sin t), y = 4 (1– cos t)(t є [ 0, 2π ]); μ =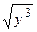 
;
16). Г: x = 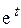(cos t + sin t), y = 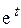(cos t – sin t) (t є [ 0, π ]); μ = ;
17). Г: x = 2 cos t – cos 2 t, y = 2 sin t – sin 2 t (t є [ 0, ]); μ = y;
18). Г: x = t cos t, y = t sin t (t є [ 0, 1 ]); μ = ;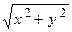
19). Г: x = 3 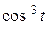, y = 3 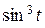(t є [- , ]); μ = ;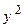
20). Г: x = 4 (cos t + t sin t), y = 4 (sin t – t cos t) (t є [ 0, π ]); μ = ;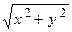
21). Г: x = 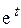(cos t + sin t), y = 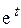(cos t – sin t) (t є [ 0, ]); μ = ;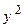
22). Г: x = 3 (t – sin t), y = 3 (1 – cos t)(t є [ 0, π ]); μ = y ;
23). Г: x = 5 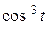, y = 5 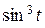(t є [ 0, ]); μ = 
;
24). Г: x = ( – 2) sin t + 2 t cos t, y = (2 – ) cos t + 2 t sin t,
(t є [ 0, π ]); μ = ;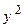
25). Г: x = t cos t, y = t sin t (t є [ 0, 2 ]); μ = ;
26). Г: x = 2 cos t – cos 2 t, y = 2 sin t – sin 2 t (t є [ 0, π ]); μ = ;
27). Г: x = cos t + t sin t, y = sin t – t cos t (t є [ 0, 2π ]); μ = | y |;
28). Г: x = 8 (t – sin t), y = 8 (1 – cos t)(t є [ 0, π ]); μ = ;
29). Г: x = 5 (cos t + t sin t), y = 5 (sin t – t cos t) (t є [ 0, ]); μ = | x |;
30). Г: x = 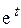(cos t + sin t), y = 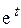(cos t – sin t) (t є [ 0, ]); μ = x.
Задача 2. Вычислить работу силового поля F вдоль дуги кривой Г:
1). F = 
, Г: y = sin x, x є [ , ];
2). F = 2 (arcsin x – x ln y) i – (2 arcsin y +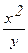 
) j,
Г: y = tg 2 x, x є [ 
, 
];
3). F =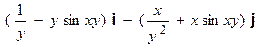 
, Г: y = 
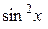, x є [ 
, ];
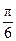4). F = [ y + ln (1 + x) ] i + (x + 1 –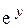 
) j, Г: y = sin 2 x, x є [ 0, ];
5). F = [sin x + cos (x + 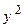)] i + 2 y cos (x + 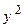) j, Г: y = sh x, x є [ 0, 
];
6). F = 
i + (y –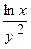 
) j, Г: y = ctg x, x є [ , 
];
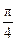7). F = (1 + cos x –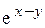 
) i +(cos y + 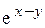) j,
Г: y = sin 2 x, x є [ , ];
8). F =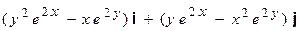 
,
Г: y = 
, x є [ 0, ];
9). F = 
, Г: y = 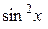, x є [ , ];
10). F =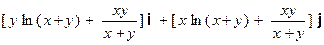 
; Г: y = 
, x є [ 0, 2];
11). F =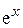 
(x sin y + y cos y) i + 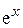(x cos y – y sin y) j;
Г: y = x, x є [ , ];
12). F = 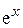(2 x + 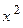+ 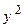) i + 2 y 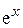j; Г: y = , x є [ 0, ];
13). F = (1 – y 
) i + j; Г: y = 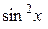, x є [ , ];
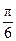14). F = (2 x – y ) i + j; Г: y = 2 x, x є [ 2, 3];
15). F = 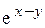(1 + x+ y) i + 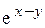(1– x – y) j;Г: y = ln x, x є [ 1, 2];
16). F = y 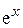i + (y + 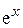) j; Г: y = ch x, x є [ 0, 4];
17). F = 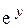i + (cos y + x 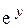) j; Г: y = , x є [ 0, ];
18). F = (2 x cos y – 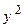sin x) i + (2 y cos x – 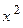sin y) j;
Г: y = 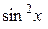, x є [ , ];
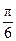19). F = [ y cos x + sin (x – y)] i + [sin x - sin (x – y)] j; Г: y = x, x є [ , ];
20). F = 2 (xy + sin y) i + (2 x cos y + 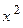) j; Г: y = 3 x, x є [ 0, 3];
21). F = 2 x cos (y + 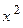) i + [sin y + cos (y + 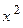)] j, Г: y = ch x, x є [ 0, 
];
22). F = (cos x + y 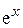) i + 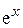j; Г: y = 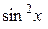, x є [ , ];
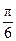23). F = (2 arcsin x +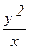 
) i – 2 (arcsin y – y ln x) j,
Г: y = ctg 2 x, x є [ π / 8, π / 6 ];
24). F = (y + 1 – 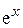) i + [ x + ln (1 + y) ] j, Г: y = sin 2 x, x є [ 0, π / 2 ];
25). F = (cos x +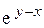 
) i +(1+ cos y – 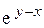) j,
Г: y = sin 2 x, x є [ π / 2, 3 / 2 π ];
26). F = 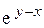(1– x – y) i + 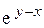(1 + x + y) j;Г: y = ln x, x є [ 1, 2 ];
27). F = [sin y + sin (x – y) ] i + [ x cos y –sin (x – y) ] j,
Г: y = 2 x, x є [ , ];
28). F = (x + 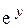) i + x 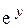j; Г: y = sh x, x є [ 0, 4];
29). F = (2 y cos x + 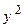) i + 2 (xy + sin x) j, Г: y = 4 x, x є [ 0, 3];
30). F = (x – 
) i + j, Г: y = tg x, x є [ , ].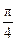
Задача 3. Найти циркуляцию Ц вектора a вдоль контура Г:
1). a = (x – z) i + (z – x) j + (x – y) k; Г: 
= 1, z = 2 (1– x);
2). a = 2 y i + 3 x j + x k; Г: = 4, x + y + z = 2;
3). a = x i – 
/ 3 j + y k; Г: 
= 1, 8 x – 4 y – 4 z = 1;
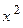4). a = x i – 2 j + y k; Г: 16 + 9 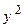= 144, z –2 x + y = 1;
5). a = – z i – x j + xz k; Г: 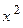+ 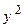= 25, z = 4;
6). a = x i – 3 j + y k; Г: 16 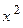+ 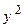= 16, z – 2 x + y = 3;
7). a = –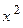 
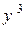i + 4 j + z k; Г: = 4, z = 4;
8). a = xy i + yz j + xz k; Г: = 9, x + y + z = 1;
9). a = x z i – j + y k; Г: = 3, z = 1;
10). a = y i – 2 x j +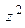 
k; Г: z = 4 () + 2, z = 6;
11). a = x i + yz j – x k; Г: = 1, x + y + z = 1;
12). a = 2 y i + 5 z j + 3 x k; Г: 2 () = 1, x + y + z = 3;
13). a = 4 x i – yz j + x k; Г: = 1, x + y + z = 1;
14). a = 2 (2 – xy) i – yz j – xz k; Г: = 4, x + y + z = 1;
15). a = 3 z i – 2 y j + 2 y k; Г: = 4, 2 x –3 y –2 z = 1;
16). a = yz i + 2 xz j + xy k; Г: = 9, z = 4;
17). a = (y – z) i + (z – x) j + (x – y) k; Г: = 4, 2 z +3 x = 6;
18). a = 2 y i – z j + x k; Г: = 1, x + y + z = 4;
19). a = 3 y i – 3 x j + x k; Г: = 9, x + y + z = 3;
20). a = (y – z) i + (z – x) j + (x – y) k; Г: = 16, 4 z + x =4;
21). a = x i + j + y k; Г: 4 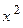+ 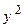= 4, 2 x – y – z = 1;
22). a = y i – x j + z k; Г: 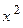+ 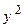= 1, z = 3;
23). a = – 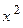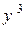i + 2 j + xz k; Г: = 2, z = 1;
24). a = 4 i + 3 x j + 3 xz k; Г: = 9, z = 3;
25). a = 4 y i – 3 x j + x k; Г: = 16, x + y + z = 4;
26). a = 2 y i + j – 2 yz k; Г: = 4, z = 2;
27). a = x z i – j + y k; Г: = 1, z = 4;
28). a = 4 x i + 2 j – x y k; Г: = 3, z = 7;
29). a = y i – x j + 2 z k; Г: = 1, z = 2;
30). a = z i + x j + y k; Г: = 4, z = 0.
