Реферат
В работе решаются семь типовых задач теории оптимизации:
1) Задача выпуклого программирования;
2,3) Задачи линейного программирования
4) Задача классического вариационного исчисления
5) Задача Больца
6) Изопериметрическая задача
7) Задача с подвижными концами
8) Задача Лагранжа
В задаче 1 методом множителей Лагранжа находится стационарная точка, далее проверяется выполнение достаточного условия минимума, которое для задач выпуклого программирования сводится к тому, что первый множитель Лагранжа (при целевой функции) должен быть отличен от нуля. В силу свойств выпуклых задач найденная точка локального минимума является одновременно точкой глобального минимума.
В задаче 2 графическим методом находится точка минимума функции. Для этого выражаются базисные элементы через свободные, используя метод Гаусса, и затем на графике, учитывая все полученные условия, находится точка минимума.
В задаче 3 используется симплекс-метод для нахождения минимума функции. Для этого выражаются базисные элементы через свободные, используя метод Гаусса, и затем составляются симплекс таблицы с последующим их пересчетом по правилам. Из конечной таблицы и находится точка минимума.
В задаче классического вариационного исчисления (задаче 4), используется уравнение Эйлера-Лагранжа и начальные условия, находится экстремаль. Далее проверяется выполнение условия глобального минимума.
В задаче Больца (задаче 5) используется уравнение Эйлера-Лагранжа, а также условия трансверсальности, находится экстремаль. Далее проверяется выполнение условия глобального минимума.
В изопериметрической задаче (задаче 6) применяется метод Лагранжа и, используя уравнение Эйлера-Лагранжа, а также начальное уравнение и краевые условия, находится экстремаль. Далее проверяется выполнение условия глобального минимума.
Для решения задачи с подвижными концами (задача 7) применяется метод Лагранжа и, используя уравнение Эйлера-Лагранжа, условия трансверсальности и стационарности, а также краевые условия, находится экстремаль. Далее проверяется выполнение условия глобального минимума.
Для решения задачи Лагранжа (задача 8) применяется метод Лагранжа и, используя уравнение Эйлера-Лагранжа, а также условия трансверсальности и начальные условия, находится экстремаль. Далее проверяется выполнение условия глобального минимума.
Содержание
Введение………………………………………………………………………….6
Основная часть…………………………………………………………………...7
Задача 1………………………………………………………..…...….……..7
Задача 2……………………………………………………………..………..9
Задача 3……………………………………………………………..………..11
Задача 4.……………………………………………………………..……….13
Задача 5.……………………………………………………………..……….15
Задача 6.……………………………………………………………..……….16
Задача 7.……………………………………………………………..……….19
Задача 8.……………………………………………………………..……….22
Заключение……………………………………………………………………….25
Список использованных источников…………………………………………...26
Введение
Каждый человек время от времени оказывается в ситуации, когда достижение некоторого результата может быть осуществлено не единственным способом. В таких случаях приходится отыскивать наилучший способ. Однако в различных ситуациях наилучшими могут быть совершенно разные решения. Все зависит от выбранного или заданного критерия.
На практике оказывается, что в большинстве случаев понятие «наилучший» может быть выражено количественными критериями – минимум затрат, минимум времени, максимум прибыли и т.д. Поэтому возможна постановка математических задач отыскания оптимального (optimum – наилучший) результата, так как принципиальных различий в отыскании наименьшего или наибольшего значения нет. Задачи на отыскание оптимального решения называются задачами оптимизации. Оптимальный результат, как правило, находится не сразу, а в результате процесса, называемого процессом оптимизации. Применяемые в процессе оптимизации методы получили название методов оптимизации. Чтобы решить практическую задачу надо перевести ее на математический язык, то есть составить ее математическую модель.
Одним из наиболее общих подходов к решению задачи поиска экстремума (локального максимума или минимума) функции при наличии связующих ограничений на ее переменные (или, как еще говорят, задачи условной оптимизации) является метод Лагранжа. Данный метод используется в задачах 1, 6, 7, 8 данной курсовой работы.
Основная часть
ЗАДАЧА 1. Решить задачу выпуклого программирования.
Составим функцию Лагранжа:
Теперь запишем условия равенства нулю частных производных функции, условие дополняющей нежёсткости и, т.к. ищется минимум функции, условие неотрицательности всех 
.
1) Рассмотрим случай 
:
→ 
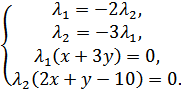
Получаем нулевые , нулевой Лагранжиан решение отсутствует
2) Рассмотрим случай 
:
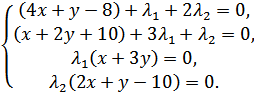
2.1) Пусть 
:
→ 
→ 
→ т. Min, т. к. выполняется условие 
и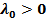 
. Так как мы решаем задачу выпуклого программирования, то точка минимума является единственной и глобальной и рассматривать остальные случаи не имеет смысла. И все же:
2.2) Пусть 
:
→ 
→ 
→ 
→ 
→ 
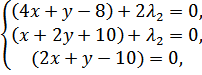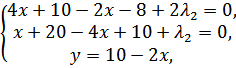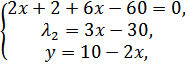- не может быть точкой минимума
2.3) Пусть 
:
→ 
→ 
→
→ 
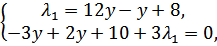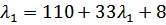- не может быть точкой минимума
2.4) Пусть 
:
→ 
→
→ 
→ 
→ 
→ 
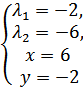
- не может быть точкой минимума.
Таким образом точка (25/7, -48/7) является точкой глобального минимума функции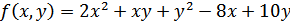 
.
ЗАДАЧА 2. Решить задачу линейного программирования графическим методом. Во всех вариантах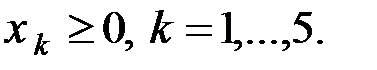 
Т.к. в условии следующей задачи первоначальная крайняя точка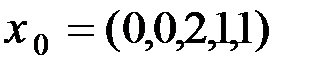 
, логично будет использовать в качестве базисных переменных x3, x4, x5 и выделить именно их, решая систему методом Гаусса. Запишем систему в матричном виде и решим, наконец, ее:
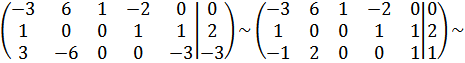
Построим график для новой системы уравнений и нанесем линию уровня:
Для получения координат точки максимума исследуемой функции линию положения нужно передвигать вправо (т.к. функция прямо пропорциональна x1) и вниз (т.к. функция обратно пропорциональна x2) до крайнего положения.
Точка максимума находится на пересечении двух прямых, задаваемых уравнениями:
Таким образом, точка M(1, 1/2) является точкой максимума данной функции.
ЗАДАЧА 3. Решить задачу № 2 симплекс-методом, используя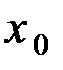 
в качестве первоначальной крайней точки.
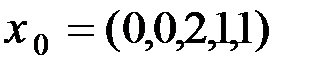
Т.к. мы будем искать максимум функции, а симплекс метод применяется для поиска минимума функции, домножим целевую функцию на минус единицу, таким образом обратив ее минимумы и максимумы.
; 
| αij | x1 | x2 | βi | |
| x3 | ||||
| x4 | -2 | |||
| x5 | -1 | |||
| f(x) | -4 | pj |
Ищем среди коэффициентов pi(коэффициентов целевой функции) pi<0, берем соответствующий этому элементу столбец (кроме столбца свободных членов). Для выбора опорного элемента необходимо найти, какой из них удовлетворит условию минимума отношения свободного члена к данному элементу: 
, причем 
После выбора опорного элемента совершаем пересчет таблицы:
- опорный элемент заменяем на единицу, деленную на опорный элемент;
- опорную строку делим на опорный элемент;
- опорный столбец делим на опорный элемент и умножаем на минус единицу;
- остальные элементы считаем по «правилу определителя» (при этом беря со знаком «+» произведение, содержащее опорный элемент) и делим на опорный элемент
- совершаем эти итерации до тех пор, пока в нижней строке все элементы (кроме свободного члена) не станут положительными.
| αij | x1 | x2 | βi | αij | x4 | x2 | βi | αij | x4 | x3 | βi | |||
| x3 | x3 | -1/2 | 3 | 3/2 | x2 | -1/6 | 1/2 | |||||||
| x4 | 2 | -2 | → | x1 | 1/2 | -1 | 1/2 | → | x1 | 1/3 | 1/3 | |||
| x5 | -1 | x5 | -1/2 | 3/2 | x5 | -1/3 | -1/3 | |||||||
| f(x) | -4 | f(x) | -2 | f(x) | 5/3 | 2/3 |
Таким образом, мы получили сходный ответ с полученным во второй задаче: точка с координатами x1=1, x2=1/2, x3=2/3, x4=-1/6, x5=1,
.
.
ЗАДАЧА 4. Решить простейшую задачу классического вариационного исчисления.
Воспользуемся уравнением Эйлера-Лагранжа для решения простейшей задачи:
.
Предположим, что:
Подставим в исходное уравнение:
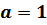
Применим краевые условия для нахождения констант:
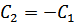
– экстремаль
Исследуем экстремаль на предмет доставления функции максимума/минимума:
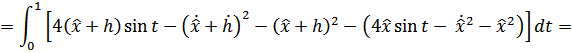
Проинтегрируем по частям: 
, где:
- точка 
является точкой максимума.
ЗАДАЧА 5. Решить задачу Больца.
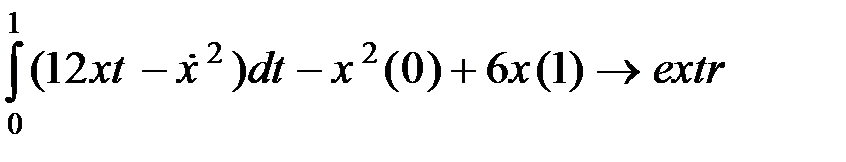
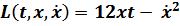- Интегрант
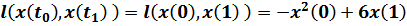- Терминант
Воспользуемся уравнением Эйлера-Лагранжа для решения задачи Больца:
.
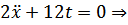
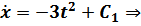
– экстремаль
Воспользуемся условиями трансверсальности:
Посчитаем каждый элемент:
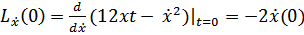
Тогда условия трансверсальности запишутся:
Мы будем использовать эти уравнения как краевые условия для нахождения констант 
.
Исследуем экстремаль на предмет доставления функции максимума/минимума:
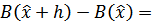(Запишем, сразу группируя интегральную и неинтегральную части)
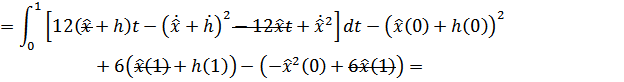
Проинтегрируем по частям: , где:
А также воспользуемся условием: 
и
в подстановке 0 и 1 (для подсчета значения элемента 
):
, 
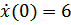– отрицательный результат – следовательно является точкой максимума.
ЗАДАЧА 6. Решить изопериметрическую задачу.
; 
, 
Воспользуемся уравнением Эйлера-Лагранжа для решения изопериметрической задачи:
.
1) 
– нет решений (Лагранжиан не м. б. равен нулю)
2) 
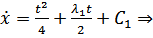
Воспользуемся краевыми условиями для нахождения констант:
, 
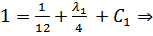
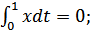- Воспользуемся уравнением для нахождения 
:
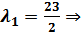
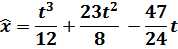
Исследуем экстремаль на предмет доставления функции максимума/минимума:
Проинтегрируем по частям: , где:
Так как 
, 
тоже должна быть равна нулю, следовательно 
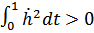– точка минимума.
ЗАДАЧА 7. Решить задачу с подвижными концами.
Выпишем, как положено, функцию Лагранжа:
Воспользуемся уравнением Эйлера-Лагранжа для решения задачи с подвижными концами:
.
Воспользуемся условиями трансверсальности:
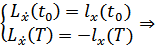
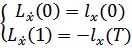Посчитаем каждый элемент:
Тогда условия трансверсальности запишутся:
Запишем условие стационарности:
Пусть 
Тогда 
также равны нулю – нет решений.
Пусть 
, тогда:
Если , найдем константы, используя краевые условия:
, 
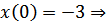
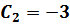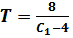
В уравнение стационарности также подставим 
, используя уравнение, написанное выше:
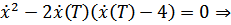
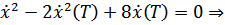
Рассмотрим 
, тогда 
а 
– что является недопустимым значением
Рассмотрим 
, тогда 
и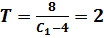 
Итак, мы получили:
, 
; 
,
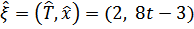Исследуем экстремаль 
на предмет доставления функции максимума/минимума:
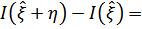
Воспользуемся и h(0)=0 (в силу наложенного ограничения на левый конец).
Также, стоит выразить значение 
из уравнения 
, помня, что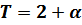 
, а 
Итак:
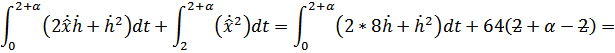
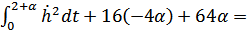
– следовательно найденная точка является точкой минимума.
ЗАДАЧА 8. Решить задачу Лагранжа.
; 
, 
, 
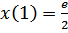Используем замену переменных 
, тогда условие запишется:
; 
, 
, 
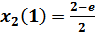
Запишем функцию Лагранжа:
1) Воспользуемся уравнением Эйлера-Лагранжа для решения задачи с Лагранжа. Оно запишется отдельно относительно x1 и x2 и образует, таким образом, систему уравнений:
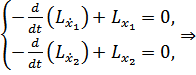
2) Воспользуемся условиями трансверсальности:
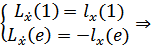
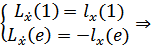
– уравнения, записанные относительно x1
– уравнения, записанные относительно x2
, 
Положим 
. Тогда из уравнений, записанных выше, получим 
из третьего уравнения условий трансверсальности, а также равенство нулю функции p(t) из второго уравнения Эйлера-Лагранжа, а как следствие и равенство нулю и (1 и 2 уравнения условий трансверсальности соответственно). Таким образом, этот вариант нам не подходит, так как для нахождения решения Лагранжиан не может быть нулевым.
Тогда, пусть :
Из уравнения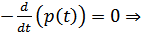 
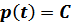
Из 
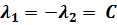
Из 
получим:
, сделаем замену 
Решим однородное уравнение:
, 
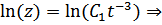
Теперь решим неоднородное:
Пусть 
. Подставим:
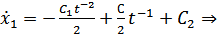
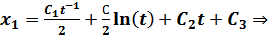
Используем краевые условия для нахождения констант:
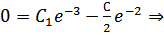
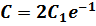
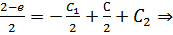
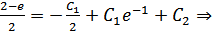
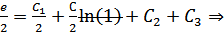
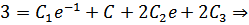
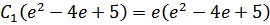
Таким образом, очевидно:
,
,
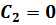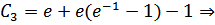
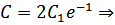
Получаем: 
, 
, 
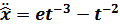
Исследуем экстремаль функции на предмет доставления ей максимума/минимума:
Интегрируем по частям:
.
Таким образом, разница оказалась больше равна нулю. Это значит, что точка 
является точкой минимума.
Заключение
В курсовой работе получены решения семи типовых задач теории оптимизации: двух конечномерных (задачи выпуклого программирования и линейного программирования) и пяти задач вариационного исчисления (простейшей задачи вариационного исчисления, задачи Больца, изопериметрической задачи, задачи с подвижными концами и задачи Лагранжа)
В результате работы над настоящей курсовой работой были достигнуты следующие цели:
1. расширен объем и углублены теоретические знания по дисциплине "Методы оптимизации";
2. закреплены практические навыки решения задач теории оптимизации;
3. получены навыки применения метода множителей Лагранжа как основного метода решения задач оптимизации с ограничениями, как конечномерных, так и бесконечномерных;
4. получен навык подготовки и оформления научно-технической документации.
Список использованных источников
1. Алексеев В.М., Тихомиров В.М., Фомин С.В. Оптимальное управление. Москва: Наука, 1979.
2. Алексеев В.М., Галеев Э.М., Тихомиров В.М. Сборник задач по оптимизации. Москва: Наука, 1984.
3. Галеев Э.М., Тихомиров В.М. Оптимизация: теория, примеры, задачи. Москва.: Эдиториал УРСС, 2000.
4. Галеев Э.М. Оптимизация: теория, примеры, задачи. Москва: УРСС, 2002.
5. Магарил-Ильяев Г.Г., Тихомиров В.М. Выпуклый анализ и его приложения. Москва.: Эдиториал УРСС, 2000.
6. Шатина А.В. Методы оптимизации. Практические занятия. М.: МИРЭА, 2012,
7. Методы оптимизации. 4-ый курс. Контрольные задания для студентов факультета Кибернетики. М.: МИРЭА, 2010.
