Симплексный метод решения задачи линейного программирования.
Общие сведения о симплексном методе.
На предыдущих лекциях мы рассмотрели основные теоремы линейного программирования, из которых следует, что если задача линейного программирования имеет оптимальное решение, то оно соответствует хотя бы одной угловой точке многогранника решений и совпадает, по крайней мере, с одним из допустимых решений. Геометрически это соответствует перебору всех угловых точек многогранника. Практическое осуществление такого перебора связано с огромными трудностями, так как для реальных задач (где число переменных на много больше 2-х) число допустимых базисных решений хотя и конечно, но очень велико.
Число перебираемых допустимых решений можно сократить, если производить перебор не беспорядочно, а с учетом изменения линейной функции, т.е. добиваться того, чтобы каждое следующее решение было лучше (или, по крайней мере, не хуже), чем предыдущее. Поясним это на примере:
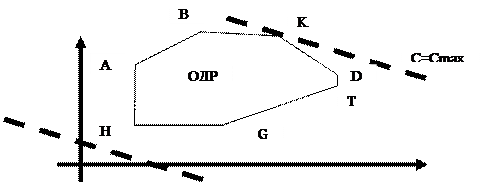
Область допустимых решений: HABКDTG. Допустим точка А соответствует исходному допустимому базисному решению. Можно в разную сторону двигаться от точки А, только в одном случае надо будет перебрать большее число угловых точек.
Идея последовательного улучшения решения легла в основу универсального метода решения задачи линейного программирования – симплексного метода.
Впервые метод был предложен американским ученым Данцигом в 1949 году, однако еще в 1939 году основные идеи методы были разработаны российским ученым Канторовичем.
Симплексный метод позволяет решить любую задачу линейного программирования. В настоящее время он используется для компьютерных расчетов. Несложные примеры с использованием симплексного метода можно решать и вручную.
Для реализации симплексного метода необходимо знать 3 основных элемента:
1. Способ определения какого-либо первоначального допустимого базисного решения;
2. Признак проверки оптимальности найденного решения.
3. Правила перехода к лучшему (точнее, не худшему) решению;
В настоящее время существует много различных модификаций симплексного метода, практически все они схожи по процедуре вычисления, отличаются лишь отдельными деталями.
Мы подробно рассмотрим наиболее простой алгоритм симплексного метода.






