Практические занятия.
Тема. Метод Крамера решения СЛУ. Решение СЛУ методом обратной матрицы.
Тема. Метод Гаусса решения СЛУ.
Системы линейных уравнений.
…Система уравнений вида: 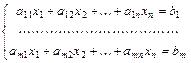 называется системой
называется системой 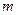 линейных уравнений с
линейных уравнений с 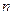 неизвестными. В матричной форме система имеет вид:
неизвестными. В матричной форме система имеет вид: 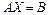 , где
, где 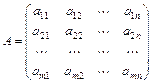 ,
, 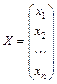 ,
, 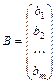 . Здесь
. Здесь 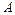 -матрица системы,
-матрица системы, 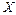 -матрица-столбец неизвестных,
-матрица-столбец неизвестных, 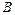 - матрица-столбец свободных членов. Если
- матрица-столбец свободных членов. Если 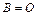 , где
, где 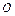 - нулевая матрица-столбец (все её элементы равны нулю), то система называется однородной, в противном случае неоднородной.
- нулевая матрица-столбец (все её элементы равны нулю), то система называется однородной, в противном случае неоднородной.
Если в системе 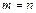 и определитель матрицы системы
и определитель матрицы системы 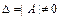 (т.е. матрица
(т.е. матрица 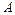 имеет обратную
имеет обратную 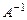 ), то система имеет единственное решение, определяемое:
), то система имеет единственное решение, определяемое:
а) по формулам Крамера: 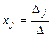 ,
, 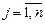 , где
, где 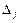 - определитель, получаемый из определителя системы
- определитель, получаемый из определителя системы 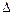 заменой
заменой 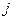 -ого столбца на столбец свободных членов;
-ого столбца на столбец свободных членов;
б ) методом обратной матрицы по формуле 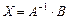 .
.
Решение произвольной системы уравнений находят методом Гаусса. Для этого составляют расширенную матрицу системы 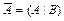 , приписывая к матрице системы
, приписывая к матрице системы 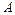 справа столбец свободных членов
справа столбец свободных членов 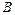 . Затем расширенную матрицу
. Затем расширенную матрицу 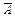 с помощью элементарных преобразований над строками и перестановкой столбцов приводят к специальному виду:
с помощью элементарных преобразований над строками и перестановкой столбцов приводят к специальному виду: 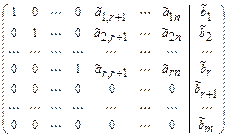 . Если хотя бы одно из чисел
. Если хотя бы одно из чисел 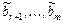 отлично от нуля, то исходная система уравнений несовместна; если
отлично от нуля, то исходная система уравнений несовместна; если 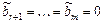 , то система совместна. Совместная система имеет единственное решение, если
, то система совместна. Совместная система имеет единственное решение, если 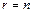 , и бесконечное множество решений, если
, и бесконечное множество решений, если 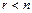 . Считая
. Считая 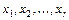 базисными неизвестными,
базисными неизвестными, 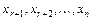 -свободными, бесконечное множество решений записывают в виде общего решения, придавая свободным неизвестным произвольные значения:
-свободными, бесконечное множество решений записывают в виде общего решения, придавая свободным неизвестным произвольные значения: 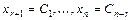 и выражая базисные неизвестные через свободные.
и выражая базисные неизвестные через свободные.
Однородная система уравнений всегда совместна, так как имеет тривиальное решение 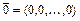 . Для существования нетривиального решения однородной системы необходимо и достаточно, чтобы
. Для существования нетривиального решения однородной системы необходимо и достаточно, чтобы 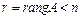 (при
(при 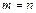 это условие означает:
это условие означает: 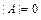 ).
).
В задачах 1.91-1.100 решить системы уравнений:
а) по формулам Крамера; б) методом обратной матрицы; в) методом Гаусса.
1.91 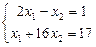 . 1.92
. 1.92 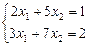 . 1.93
. 1.93 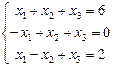 . 1.94
. 1.94 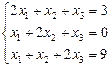 .
.
1.95 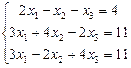 . 1.96
. 1.96 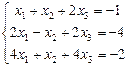 . 1.97
. 1.97 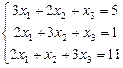 .
.
1.98 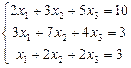 . 1.99
. 1.99 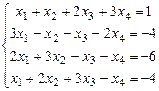 . 1.100
. 1.100 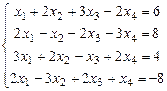 .
.
В задачах 1.101-1.114 решить системы уравнений методом Гаусса.
1.101 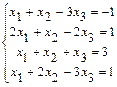 . 1.102
. 1.102 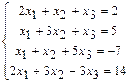 . 1.103
. 1.103 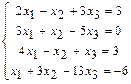 . 1.104
. 1.104 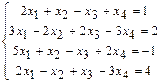 . 1.105
. 1.105 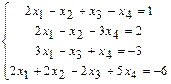 . 1.106
. 1.106 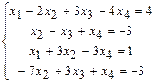 .
.
1.107  . 1.108
. 1.108 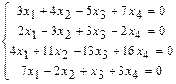 . 1.109
. 1.109 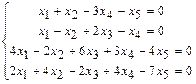 .
.
1.110  . 1.111
. 1.111 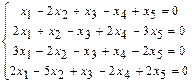 .
.
1.112 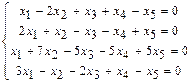 . 1.113
. 1.113 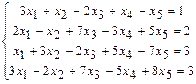 .
.
1.114 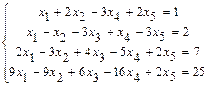 .
.
Ответы.
1.91 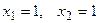 1.92
1.92 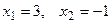 1.93
1.93 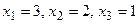 1.94
1.94 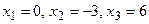
1.95 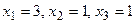 1.96
1.96 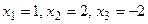 1.97
1.97 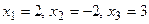
1.98 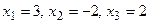 1.99
1.99 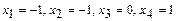 1.100
1.100 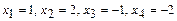
1.101 Несовместна. 1.102 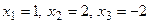 1.103
1.103 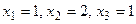 1.104 Несовместна.
1.104 Несовместна.
1.105 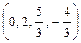 1.106
1.106 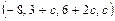 1.107
1.107 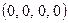 1.108
1.108 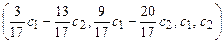
1.109 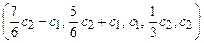 1.110
1.110 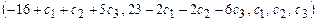
1.111 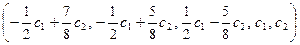 1.112
1.112 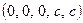 1.113. Несовместна.
1.113. Несовместна.
1.114. Несовместна.






