7.91. 7.92. 7.93. 7.94. 7.95.
7.96. 7.97. 7.98. 7.99. 7.100.
7.101. 7.102. 7.103. 7.105. 7.108. 7.109. 7.110. 7.112. 7.113. 7.114. 7.115. 7.116.
Интегрирование гиперболических функций аналогично интегрированию тригонометрических функций. При этом используются формулы:  ;
;  ;
;  ;
;  .
.
В задачах 7.119-7.130 найти следующие интегралы от гиперболических функций:
7.119. 7.120. 7.121. 7.123. 7.124.
Интегралы вида  , где
, где  -рациональная функция своих аргументов,
-рациональная функция своих аргументов,  -целые числа, вычисляются с помощью подстановки
-целые числа, вычисляются с помощью подстановки  , где
, где  - наименьший общий знаменатель дробей
- наименьший общий знаменатель дробей  .
.
Вычисление интегралов вида  , где
, где  -рациональная функция своих аргументов, выделением полного квадрата в квадратном трёхчлене
-рациональная функция своих аргументов, выделением полного квадрата в квадратном трёхчлене  и заменой
и заменой  , сводится к вычислению интегралов вида: 1)
, сводится к вычислению интегралов вида: 1)  ; 2)
; 2) 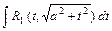 ; 3)
; 3)  , где
, где  - рациональная функция своих аргументов. Последние интегралы, соответственно, с помощью тригонометрических или гиперболических подстановок: 1)
- рациональная функция своих аргументов. Последние интегралы, соответственно, с помощью тригонометрических или гиперболических подстановок: 1)  или
или  ; 2)
; 2)  или
или  ; 3)
; 3)  или
или 
приводятся к интегралам вида  или
или  , где
, где  - рациональная функция своих аргументов
- рациональная функция своих аргументов
В задачах 7.131-7.140 найти следующие интегралы от иррациональных функций:
а); б); в). 7.132а); б).
7.133а)  ; б)
; б)  ; в)
; в)  . 7.134а)
. 7.134а)  ; в)
; в) 
В).






