Определение 10.8. Квадратная матрица  называется обратной для квадратной матрицы
называется обратной для квадратной матрицы  , если
, если
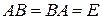 . (10.5)
. (10.5)
Если для квадратной матрицы существует обратная, то обе эти матрицы имеют одинаковый порядок.Матрицу, обратную матрице  , впредь будем обозначать
, впредь будем обозначать 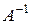 .
.
Теорема 10.3 (существования и единственности ). Квадратная матрица  имеет обратную тогда и только тогда, когда
имеет обратную тогда и только тогда, когда  невырождена, т.е.
невырождена, т.е. 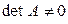 . В случае существования обратная матрица определяется единственным образом:
. В случае существования обратная матрица определяется единственным образом:
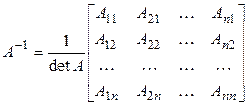 , (10.6)
, (10.6)
где 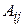 – алгебраическое дополнение к элементу
– алгебраическое дополнение к элементу 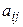 матрицы
матрицы  .
.
Таким образом, чтобы для квадратной матрицы  найти обратную, следует составить матрицу из алгебраических дополнений к элементам матрицы
найти обратную, следует составить матрицу из алгебраических дополнений к элементам матрицы  , транспонировать ее и все элементы разделить на
, транспонировать ее и все элементы разделить на 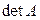 .
.
Пример 10.23. Пусть  – квадратная матрица,
– квадратная матрица, 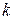 – некоторое натуральное число,
– некоторое натуральное число, 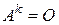 , но
, но 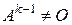 . Доказать, что
. Доказать, что
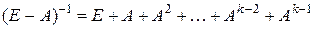 .
.
∆ Введем обозначения 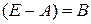 ,
, 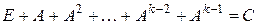 и найдем произведение
и найдем произведение 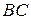 . Учитывая, что все натуральные степени квадратной матрицы перестановочны между собой, а также, что единичная матрица перестановочна с любой, получаем:
. Учитывая, что все натуральные степени квадратной матрицы перестановочны между собой, а также, что единичная матрица перестановочна с любой, получаем:
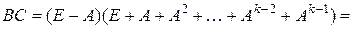
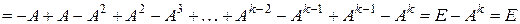
Таким образом, матрицы  и
и 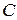 удовлетворяют определению 10.8. Значит,
удовлетворяют определению 10.8. Значит, 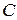 – обратная к
– обратная к  . В силу единственности обратной матрицы
. В силу единственности обратной матрицы 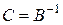 , что и требовалось доказать. ▲
, что и требовалось доказать. ▲
Пример 10.24. Найти матрицу, обратную к невырожденной матрице второго порядка 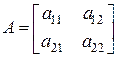 .
.
∆ Находим алгебраические дополнения 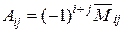 . Вспомните, что первый индекс обозначает номер вычеркиваемой строки, а второй – номер вычеркиваемого столбца. Таким образом:
. Вспомните, что первый индекс обозначает номер вычеркиваемой строки, а второй – номер вычеркиваемого столбца. Таким образом:
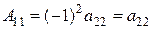 ,
, 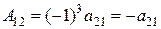 ,
,
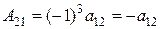 ,
, 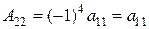 .
.
Составляем обратную матрицу, следуя формуле (10.6):
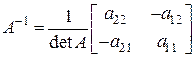 . ▲
. ▲
Из полученного результата получаем следующее
правило построения обратной матрицы второго порядка: элементы на главной диагонали меняем местами, у остальных меняем знак, и все элементы делим на определитель.
Пример 10.25. Проверить, имеет ли матрица  обратную и, если имеет, то найти ее:
обратную и, если имеет, то найти ее:
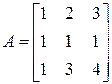 .
.
Вычислим определитель матрицы  по правилу треугольников:
по правилу треугольников: 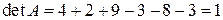 . Матрица невырождена, значит, обратная к ней существует. Находим алгебраические дополнения:
. Матрица невырождена, значит, обратная к ней существует. Находим алгебраические дополнения:
 ,
, 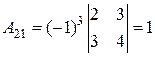 ,
, 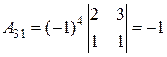 ,
,
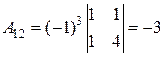 ,
, 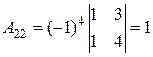 ,
, 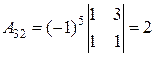 ,
,
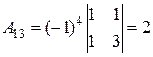 ,
, 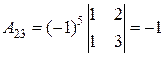 ,
, 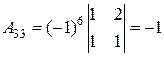 .
.
Составляем обратную матрицу:
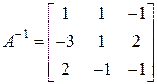 .
.
Конечно, вы должны научиться для матрицы третьего порядка устно считать алгебраические дополнения, а не расписывать так подробно. Для проверки правильности вычислений можно, например, найти произведение 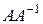 :
:
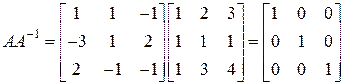 .
.
Так как оно равно единичной матрице, то обратная найдена верно. ▲
Свойства обратных матриц. Если  и
и  – невырожденные квадратные матрицы одного и того же порядка и
– невырожденные квадратные матрицы одного и того же порядка и 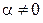 , то справедливы следующие равенства:
, то справедливы следующие равенства:
1. 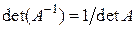 ; 2.
; 2. 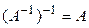 ; 3.
; 3. 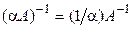 ;
;
4. 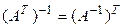 ; 5.
; 5. 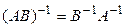 .
.
Пример 10.26. Известно, что 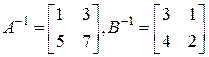 . Найти следующие матрицы: а)
. Найти следующие матрицы: а)  ; б)
; б) 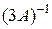 ; в)
; в) 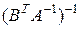 .
.
∆ Используем свойства обратной матрицы и правило построения обратной матрицы второго порядка.
а) Так как 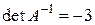 , то
, то  .
.
б) 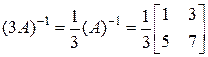 .
.
в) Согласно свойствам обратной матрицы
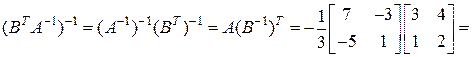
 . ▲
. ▲
Определение 10.9. Матричными уравнениями называются уравнения вида 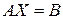 ,
, 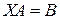 ,
, 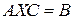 , где
, где 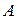 ,
,  и
и 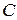 – заданные матрицы,
– заданные матрицы, 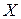 – искомая.
– искомая.
Матрица 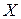 называется решением матричного уравнения, если при подстановке в него она обращает уравнение в верное равенство.
называется решением матричного уравнения, если при подстановке в него она обращает уравнение в верное равенство.
Пример 10.27. Решить следующие матричные уравнения:
а) 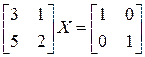 ; б)
; б) 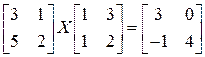 ; в)
; в) 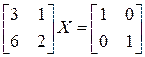 ; г)
; г) 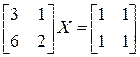 ; д)
; д) 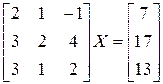 ; е)
; е) 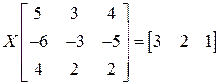 .
.
∆ а) В буквенных обозначениях уравнение имеет вид: 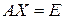 . Единственная матрица, которая может удовлетворять этому уравнению, это
. Единственная матрица, которая может удовлетворять этому уравнению, это 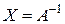 . Так как
. Так как 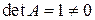 , то
, то 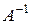 существует. Итак,
существует. Итак, 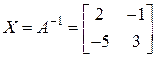 (для матрицы второго порядка обратную находим по известному правилу).
(для матрицы второго порядка обратную находим по известному правилу).
б) Это уравнение имеет вид 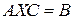 , где
, где 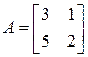 ,
, 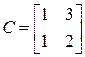 ,
, 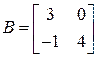 . Так как
. Так как 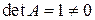 ,
, 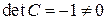 , то обе эти матрицы невырождены, а значит, имеют обратные:
, то обе эти матрицы невырождены, а значит, имеют обратные:
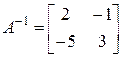 ,
, 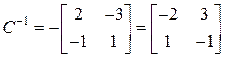 .
.
Если все уравнение умножим слева на  (слева – это значит левый сомножитель), а справа – на
(слева – это значит левый сомножитель), а справа – на  , получим:
, получим:
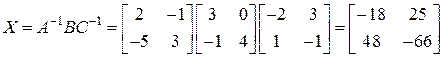 .
.
в) Уравнение имеет вид 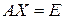 , причем
, причем 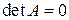 . Если уравнение имеет решение, то
. Если уравнение имеет решение, то 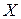 – квадратная матрица второго порядка, причем
– квадратная матрица второго порядка, причем 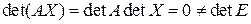 . Получили противоречие. Это значит, уравнение решения не имеет.
. Получили противоречие. Это значит, уравнение решения не имеет.
г) Уравнение имеет вид: 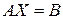 . Так как
. Так как 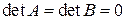 , то противоречия нет, но решать уравнение с помощью обратной матрицы нельзя. Если решение существует, то
, то противоречия нет, но решать уравнение с помощью обратной матрицы нельзя. Если решение существует, то 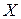 – квадратная матрица второго порядка. Пусть
– квадратная матрица второго порядка. Пусть 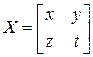 . Заданное уравнение
. Заданное уравнение 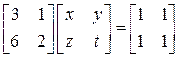 приводит нас к системе
приводит нас к системе
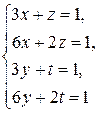 ,
,
которая, очевидно, решения не имеет. Поэтому и матричное уравнение решения не имеет.
д) Уравнение имеет вид: 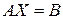 . Найдем
. Найдем 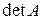 по правилу треугольников:
по правилу треугольников:
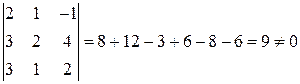 .
.
Значит, матрица 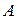 имеет обратную. Умножая обе части уравнения слева на
имеет обратную. Умножая обе части уравнения слева на 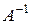 , получаем
, получаем 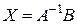 . Переходим к вычислениям:
. Переходим к вычислениям:
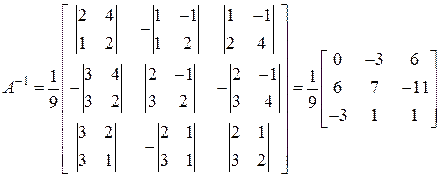 ,
,
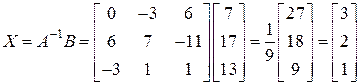 .
.
е) Уравнение имеет вид: 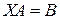 ,
,
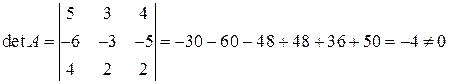 ,
,
значит, существует
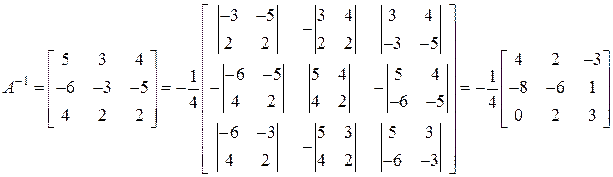 Умножая все уравнение справа на
Умножая все уравнение справа на 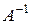 , получаем:
, получаем:
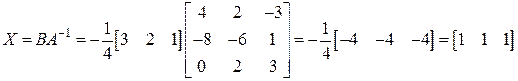 .▲
.▲






