Дисперсионный анализ наследуемости жирномолочности

Луч

Ветер

Алмаз

Число градаций r=3

4,2 4,2 3,8 3,9 3,8 3,8

х 4,3 4,4 4,0 4,1 3,8 3,9

4,4 4,2 3,0

n_i 5 5 5 N =15

 

∑_x 21,5 20,0 19,2 ∑∑_x= 60,7

 

Xi 4,3 4,0 3,84 X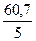_∑ = =4,05

Xi-- X_∑ +0,25 --0,05 --0,21 C_y=∑n_i(Xi-- X_∑)²

=0,545

x—Xi -0,1 -0,1 -0,2 -0,1 -0,04 -0,04 C_p=∑(x—Xi)²

0 +0,1 0 +0,1 -0,04 +0,06 =0,152

+0,1 +0,2 +0,06

x-- X_∑ +0,15 +0,15 -0,25 -0,15 -0,25 -0,25 C_f=∑(x- X_∑)²

+0,25 +0,35 -0,05 +0,05 -0,25 -0,15 =0,6975

+0,35 +0,15 --0,15

 

паратипическую дисперсию C_p —внутригрупповую сумму квадратов — показатель разнообразия дочерей быков по жирномолочности по формуле C_p=∑(x—Xi)²

С_p = (-0.1)² + (-0.1)² + (-0,1)² + • • • + (+0,06)² + (+0,06)² =
= 0,04 + 0,10 + 0,012=0,152;

фенотипическую дисперсию С_f —показатель общегo фенотипического разнообразия признака по формуле: C_f=∑(x- X_∑)²

С_f = (+0,15)² + (+0,15)² + (0,25)² ₊ (0,35)² +... + (-0,15)² +

+ (0,15)² = 0,3525 + 0,1125 + 0,2325=0,6975.

С_f=С_у + С_p,

С_f= 0,5455 + 0,152= 0,6975. С_f= 0,6975.

Коэффициент наследуемости вычисляют по формуле:

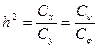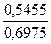h²= =0,78

Критерий достоверности наследуемости вычисляется по

формуле:

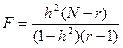F=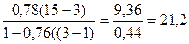

v₁ =N-1, v₁=3-1=2, v₂ =N-r, v₂=15-3=12

 

Полученное значение F = 21,2 больше табличного F_st,, следовательно, h² =0,78 достоверно при Р = 0,999.

Контрольные вопросы

1. Что такое генеральная совокупность?

2. Что такое выборки, как они составляются?

3. Как составляется вариационный ряд?

4. Какие бывают типы распределения и вариационных кривых?

5. Перечислите средние величины и их использование.

6. Как вычисляется средняя арифметическая величина в малых и больших выборках?

7. Какими свойствами обладают средние величины?

8. Какие показатели характеризуют разнообразие признаков?

9. Как вычисляется среднее квадратическое отклонение в малых ибольших выборках?

10. Как вычисляется среднее квадратическое отклонение для альтернативных признаков?

11. Как вычисляется коэффициент фенотипической корреляции амалых и больших выборках?

12. В чем заключается различие связи между признаками при по­ложительных и отрицательных значениях коэффициента корре­ляции?

13. Как вычисляется коэффициент корреляции для альтернативных признаков?

14. В каких случаях используется коэффициент ранговой корреля­ции?

15. Приведите формулы вычисления коэффициентов генетической корреляции.

16. Что характеризуют коэффициенты регрессии? В чем различиемежду коэффициентами R_x/_v и R_y/_xl

17. В чем различие между коэффициентами т и Ю

18. Что такое ошибки репрезентативности? Чем отличаются они от ошибок измерения и вычисления?

19. Как вычисляют ошибку средней- арифметической величины?

20. Приведите формулы вычисления ошибок о, Со, т, К.

21. Как изменяется величина гпх при изменении объема выборки и величины сигмы?

22. Что такое доверительные вероятности?

23. Какие доверительные вероятности можно использовать в биоло­гических, зоотехнических и ветеринарных исследованиях?

24. Как определяется -достоверность выборочных показателей?

25. Как оценивается достоверность разности между средними вели­чинами двух выборок?

26. Что такое критерий соответствия (хи-квадрат) и как он исполь­зуется в генетических исследованиях?

27. В чем заключается цель дисперсионного анализа? Что называет­ся общей, факториальной и остаточной дисперсией?

28. Какие бывают дисперсионные комплексы? Чем они характери­зуются?

29. Как составляют однофакторный дисперсионный комплекс и вы­числяют вспомогательные величины?

30. Какие показатели используются для оценки достоверности влия­ния изучаемого фактора?

 

ТЕМАТИКА И ВОПРОСЫ