ИЗОБРАЖЕНИЕ. Занятие 1.. Признаки у сельскохозяйственных животных делятся на количест­венные и качественные. К количественным признакам относятся удой молока, настриг

Занятие 1.. Признаки у сельскохозяйственных животных делятся на количест­венные и качественные. К количественным признакам относятся удой молока, настриг шерсти, содержание жира и белка в молоке, количество эритроцитов в кро­ви и другие, выражаемые числами в определенных еди­ницах измерения (кг, см, мм, г и т. д.). К качествен­ным относятся признаки, которые могут иметь только два или несколько состояний, выражаемые словами, на­пример: черная и белая масть, комолая и рогатая, тип гемоглобина в сы­воротке крови (А, В и АВ), тип шерсти (тонкая, грубая, полутонкая, полугрубая).

В группе особей, взятых для изучения, различные вариации признаков встречаются неодинаковое число раз. Частота проявления определенных значений при­знака в совокупности называется распределением.

В биометрии различают следующие типы распреде­ления; нормальное, биномиальное, Пуассона, асиммет­ричное, эксцессивное, трансгрессивное и др. Наиболь­шее значение в биологии имеют первые три.

Литература:

Вид занятия – лабораторно- практическое. Время – 2 часа.

Цель занятия. Ознакомиться с различными типами распределения признаков и научиться изображать их графически. На основе вариационных кривых уметь распознавать характер распределения признаков.

Материальное обеспечение. Раздаточный материал, линейки, лекало, калькуляторы.

Содержание и методика проведения занятия. Распределение признака можно изобразить в виде вариационного ряда, вариационной кривой и гисто­граммы.

Пример. При изучении генеральной совокупности коров по суточному удою составлена следующая выбор­ка, численность 100 голов (объем выборки и —100).

Суточный удой коров.

21,9; 21,4; 27,7; 17,0; 12,3; 21,7; 23,4; 25,7; 21,2; 20,3;

23,8; 24,1; 26,9; 21,4; 20,7; 18,5; 22,5; 23,0; 18,5; 25,7;

20,1; 21,3; 15,7; 24,8; 19,3; 22,2; 22,9; 14,9; 26,1; 20,5;

14,6; 27,8; 22,4; 16,7; 22,9; 25,3; 22,7; 19,7; 15,2; 21,3;

22,1; 20,5; 19,7; 24,5; 29,6; 22,3; 19,1; 23,5; 25,9; 17,2;

15,5; 18,1; 23,9; 25,4; 20,4; 13,2; 19,6; 24,4; 18,2; 24,8;

24,2; 20,9; 20,1; 16,5; 20,9; 23,2; 27,2; 21,1; 26,3; 18,6;

17,2; 17,8; 31,2; 25,0; 20,7; 18,3; 23,7; 16,1; 16,2; 21,6;

23,0; 20,7; 25,3; 13,9; 17,3; 21,8; 14,1; 19,0; 21,9; 18,7;

28,5; 21,2; 19,9; 24,8; 22,7; 16,4; 20,6; 23,5; 22,2; 19,5.

Для построения вариационного ряда, прежде всего, следует найти лимиты — минимальное и максимальное значения вариант. В приведенной выборке они выделе­ны. Лимиты указывают на общий размах разнообразия признака.

В данном примере минимальная варианта (Х_min) = 12,3 кг, максимальная (Хmax)=31,2 кг. Для составления вариационного ряда нужно найти величину классового промежутка (/С), которая опреде­ляется следующим образом:

(1)

Число классов устанавливается в зависимости от степени точности, с которой ведется обработка, и числа объектов в выборке. Удобно иметь следующее число классов: при объеме выборки от 30 до 60 — 6—8 клас­сов, при объеме от 61 до 100 — 7—8 классов, при объеме от 101 и более —9—12 классов. В данном примере рас­считываются 10 классов.

Полученное число целесообразно округлить до целого. Округлив 1,89, получим K = 2.

Составление классов проводится следующим образом. Минимальную величину Х_min = 12,3 округляем до меньшего круглого числа (12), которое будет нижней границей первого класса. Прибавляя к ней величину классового промежутка (2 кг), находим нижнюю границу второго класса (14). Путем прибавления к каждому классу классовый промежуток находят нижнюю границу последующих классов, которые будут 16, 18, 20, 22 и т. д.

Чтобы варианта не попала на границу между двумя классами, условно обозначают, к какому классу относится пограничная величина. С этой целью уменьшают верхнюю границу каждого класса на величину, равную 0,1 точности измерения признака. Уменьшая верхние границы на 0,1 кг, получаем границы первого класса: 12,0 – 13,9, 14, 0 – 15,9, 16,0 – 17,9 и т. д. Затем определяем величину средины классов (W). Средина класса равна полусумме нижних границ последующих классов (12+14):2=13, (14+16):2=15, или путем прибавле­ния к нижней границе половины классового промежутка (12+1=113 и т. д.).

Установив границы классов, приступают к разноске вариант по классам, для чего составляют таблицу из четырех граф и числа строк, равного числу классов (табл. 1). В первую графу выносят границы классов, во вторую – средины классов, в третью разносят варианты, в четвертой суммируют данные разноски для установления количества вариант в каждом классе. Количество вариант в классе называют часто­тами и обозначают символом f.

Разноска по классам данных по суточному удою ко­ров приведена в таблице 1.

1. Разноска по классам данных суточного удоя 100 коров

 

Границы классов	Средина классов	Частота f	Границы классов	Средина классов	Частота f
12,0-13,9			22,0-23,9
14,0-15,9			24,0-25,9
16,0-17,9			26,-27,9
18.0-19.9			28,0-29,9
20.0-21,9			30,0-31,0

∑_f =n=100

Для проверки, не пропущены ли при разноске от­дельные ва-рианты, нужно суммировать все показатели графы «Частоты». Их сумма (∑_f) должна быть равна общему числу вариант выборке (п). В данном при­мере ∑f_f =n=100.

Двойной ряд чисел, отражающий распределение ва­риант по

классам, называется вариационным рядом.

В разобранном случае вариационный ряд можно записать следующим образом:

Классы (W), кг 13 15 17 19 21 23 25 27 29 31

Частоты (f) 3 6 10 15 24 19 14 6 2 1

Вариационный ряд можно изобразить графически в виде гистограммы или в виде линейной кривой (полигон распределения). Для этого, используя систему коорди­нат, строят график: на горизонтальной оси (ось абс­цисс) откладывают границы классов, на вертикальной (ось ординат) – частоты. Изобразив частоты каждого класса в виде столбиков, получают ступенчатую фигуру, называемую гистограммой. Во втором случае при пересечении перпендикуляров, восстановленных из значений средины классов с горизонтальными линиями, проведенными из соответствующих их частот, ставят точки, которые затем соединяют ломаной линией, называемой вариационной кривой (рис. 1).

Рис. 1 Графическое изображение вариационного ряда по удою:

А— гитограмма, Б— линейная кривая

 

При нормальном распределении кривая симметрич­на к перпендикуляру, опущенному из ее вершины на ось абсцисс '(рис. 2). Ветви нормальной кривой подхо­дят к оси абсцисс, не сливаясь с ней. Нормальная кри­вая в зависимости от разнообразия признака может иметь три формы – высокую, плоскую и низкую (рис. 3).

Рис. 2. Нормальная кривая Рис. 3. Типы нормальных
распределения. кривых в зависимости от

разнообразия признаков.

 

Биномиальной называют теоретическую кривую, по­строенную по коэффициентам бинома Ньютона. Биномиальное распределение можно составлять и по альтернативным (качественным) признакам.

Пример. При изучении соотношения полов ягнят у 231 овцематки породы прекос получено следующее распределение (по А. Шацкому):

Число баранчиков (р). 0123 4 5 6 7 8 9 10

Число ярочек (q). 10 9 8 7 6 5 4 3 2 1 0

Число матерей (n_i)... 0 4 3 33 45 56 44 28 14 3 0

Всего маток n=∑ _nii =231

Распределение альтернативных признаков имеет прерывистый характер.

Среднее число баранчиков на приплод от каждой матки составило:

Х= (4х1+3х2+33х3+45х4+56х5+44х6+28х7+14х8+9х3+

10х0): 231 = 1178:231 =5,1 гол.

Доля баранчиков в потомстве 231 матки: р =1117:(10 х 231)=0,51.

Доля ярочек в потомстве 231 матки: q=1 - р=1 - 0,51=0,49

(р, q — частоты альтернативных признаков).

 

Используя формулу бинома Ньютона (р+q)ⁿ, опре­деляют теоретическое распределение.

В данном примере теоретическое биномиальное рас­пределение будет следующим:

Число баранчиков в приплоде 0 1 2 3 4 5 6 7 8 9 10

Распредел. матерей (фактич.) 043 33 45 56 44 28 14 3 1

Распредел. матерей (теоре­т.) 0 2 10 27 48 57 48 27 10 2 0

Биномиальная кривая может быть симметричной (при р = q=0,5) и асимметричной. Теоретическая бино­миальная кривая довольно близка к кривой фактиче­ского распределения (рис. 4).

 

 

Рис. 4. Биноминальное распределениеприплода разных маток из 10 ягнят по числу баранчиков.

I-теоретическое распредеение,эмпирическоераспределение.

Распределение Пуассона используется при изучении редких событий, происходящих одиь или небольшое число раз на 1 тыс., 10 тыс. и более обычных явлений (например, появление альбиносов в популяции, появление уродов, мутаций, рож-дение монозиготных близнецов).

В распределении Пу­ассона вариациями служат число редких событий, а ча­стотами— число больших групп, в которых произошло редкое событие.

Пример. В группе из 100 коров каждая корова имела по 4 отела. Среди них двойневые отелы имели всего 10 коров. Вариационный ряд распределения коров по количеству двойневых отелов имеет следующий вид:

Число двойневых отелов (х +).. 0123

Число коров (Р)..................................... 90 6 3 1

Всего 100

Эксцессивные кривые. Составим вариационный ряд по многоплодию 76 янтарь-сапфировых норок (по чис­лу щенков в помете). Составлена следующая выборка. Число щенков в помете янтарь-сапфировых норок: 5, 4, 4, 2, 8, I, 6, 4, 3, 4, 4, 4„ б, 4, 5, 2, 4, 7, 4, 6, 5, 6, 4, 5, 4, 4, 8, 4, 5, 4, 4, 5, 4, 3, 4, 5, 4, 5, 4, 4, 7, 3, 4, 5, 4, 5, 4, 4, 5, 3, 4, 4, 4, 4, 7, 5, 3, 6, 4, 9, 4, 4, 6, 4, 2, 6, 4, 2, 4, 5, 4, 4, 4, 4, 3, 4.

Общее число вариант п =76. Минимальное и макси­мальное значение вариант: lim=l—9 (эти варианты в выборке выделены).

Классы обозначают число щенков в каждом помете, частоты — число пометов. К первому классу должны быть отнесены норки, в помете которых был 1 щенок, ко второму классу — с двумя щенками и т. д. Всего 9 классов. После разноски вариант получится следую­щий вариационный ряд:

 

Классы (число щенков) (w) 1 2 3 4 5 6789

Частоты (число пометов) (/) 1 4 6 39 13 7 3 2 1

 

Следует отметить существенное различие между ва­риационными рядами (по суточным удоям коров и чис­лу щенков в помете норок). В первом случае варианта (суточный удой) может принимать любые значения между лимитами.

Отдельную варианту в зависимости от точности измерения можно записать, например, как 19 кг или при большей точности 19,1 или 19,12 кг.

 

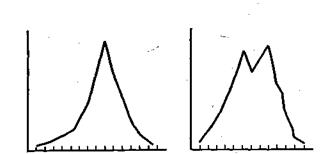
Рис. 5. Типы эксцессивных кривых:

А — эксцесс положительный; Б — эксцесс отрицательный.

Рис. 6. Типы ассиметрии

А Б

левая положительная правая отрицательная

 

 

Рис. 7. Трансгрессивные кривые

Изу­чаемый признак варьирует непрерывно. Во втором слу­чае признак изменяется прерывисто (дискретно). Число щенков в помете отдельной самки может выражаться только целым числом (1, 2 или...9). При составлении распределения признаков видно отклонение от нормаль­ного распределения, при сохранении симметричности ряда наблюдается скопление частот в центральных клас­сах. Кривая имеет вид острой пирамиды. Такое рас­пределение называется эксцессивным (эксцесс положи­тельный). При отрицательном эксцессе в центре распре­деления имеется вместо вершины впадина, в результа­те чего образуется двувершинная кривая (рис. 5).

Асимметричные ряды и кривые могут быть в резуль­тате нарушения принципа случайности при отборе жи­вотных в выборку, при большой неоднородности сово­купности, из которой берется выборка, или по объектив­ной биологической причине. Типы асимметричных кри­вых бывают правыми отрицательными и левыми поло­жительными (рис. 6).

Трансгрессивные ряды и кривые (рис. 7) имеют до­стоверно различающиеся средние арифметические вели­чины. Часть классов у них общая. Левое крыло одной кривой пересекается правым крылом другой кривой (на­пример, сравнение вариационных рядов при дигибридном скрещивании во втором поколении).

Занятие 2. ВЫЧИСЛЕНИЕ СРЕДНИХ ВЕЛИЧИН

Цель занятия. Усвоение методов вычисления средних величин в зависимости от поставленных задач и числа животных в выборке.

Методические указания. Средние величины — важ­ные биометрические показатели, используемые в науке и практике. Средняя арифметическая является основ­ным показателем, характеризующим совокупность по величине изучаемого признака. Свойства средних величин: срединное расположение между минимальным и максимальным значениями признака, абстрактность и единство суммарного действия.

В зависимости от поставленных целей в биологии используются несколько средних величин: средняя ариф­метическая, средняя взвешенная, средняя геометриче­ская, средняя гармоническая.

Вычисление средней арифметической (X) в малочисленных выборках. Средняя арифметическая величина в малочисленных выборках вычисляется прямым способом, который заключается в суммировании всех вариант (x₁+х₂+х₃+…х_n) с после­дующим делением суммы на число вариант в совокуп­ности (п):

 

(3)

где ∑x —сумма вариант. Формула (2) является наиболее точным способом вычисления X.

В группе из пяти ягнят живая масса отдельных яг­нят составляла: х₁ —5, х₂ —6, х₃ —3, х₄ —7, х₅ —4 кг. Средняя арифметическая для этой группы вычисляется по формуле (2).

Вычисление средней арифметической в многочисленных выборках. Прямой метод вычисления X при большом числе вариант при отсут­ствии вычислительной техники требует много труда. Поэтому при биометрической обработке многочислен­ных выборок используются другие методы.

Ниже рас­сматривается вычисление Х-способом произведений. При этом способе для вычисления средней арифмети­ческой величины используются вариационные ряды. Вы­числение проводится по формуле:

Х=А + ь (3), или (4)

где А — произвольно выбираемая условная средняя; Ь — поправка, которую нужно прибавить к А для получения Х.

 

Для вычисления средней арифметической величины по суточному удою коров выписываем вариационный ряд данного признака (табл. 2).

Затем надо выбрать условную среднюю (А). В ка­честве таковой обычно берут значение середины того класса, в который входит наибольшее число вариант. В данном примере Л=21 кг молока. Чтобы с помощью условной средней А вычислить среднюю арифметическую, по формуле (2) нужно найти поправку Ь.

Для этого в третьей графе таблицы 2 от­мечают, на сколько классовых промежутков отклоняет­ся от условной средней середина каждого из класса.

1. Вычисление средней арифметической