Изучение статистических закономерностей в ядерной физике
Цель работы: получить экспериментальные распределения случайной величины, сравнить их с теоретическими распределениями Пуассона и Гаусса. Приборы и принадлежности: детектор частиц (счетчик Гейгера), снабженный пересчетным устройством; в качестве источника излучения служит космический фон.
Особенности измерений в ядерной физике, вывод рабочих формул
Отличительной чертой ядерно-физических процессов является дискретность. Практически все величины в ядерной физике (заряд ядра, энергия, момент импульса и др.) не могут быть произвольными, они могут принимать только отдельные, строго определенные значения, следовательно, такими же будут и результаты измерений. Зачастую, кроме того, результат измерения имеет дискретную природу по самому своему смыслу, например, число частиц, зарегистрированных детектором, или число радиоактивных превращений в образце в заданном интервале времени. Тесно связанным со свойством дискретности оказывается вероятностный характер процессов в ядерной физике. Из-за этого во многом меняется и понятие о точности измерений, оценке их погрешностей. Понятие вероятности становится неотъемлемой характеристикой процесса, явления. Это проявляется в том, что численные значения измеряемых величин могут испытывать случайные, непредсказуемые колебания, которые называют флуктуациями. Поэтому не имеет смысла ставить вопрос о строго определенных значениях многих измеряемых величин, но вполне законен вопрос о вероятности получить в результате измерения то или иное значение измеряемой величины. Например, при измерении числа-частиц, зарегистрированных детектором, нельзя сказать, что это число будет иметь строго определенное значение. Но можно говорить о вероятности данного значения. Поэтому обработка результатов измерений требует теперь привлечения основных представлений о вероятностях.
Вероятность можно представить как частоту, с которой данное событие будет происходить при многократном повторении опыта. Предположим, что при измерении числа частиц, зарегистрированных счетчиком за определенное время, получен ряд чисел при многократном (N) включении счетчика. Число А при этом повторилось l (A) раз. В этом случае вероятность появления в измерениях числа А можно оценить следующим образом:
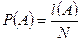. (1)
Очевидно, что для любой вероятности справедливо соотношение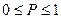 
, причем событие с вероятностью 
, т.е. наблюдается всегда, называется достоверным, а событие с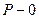 
, т.е. не наблюдавшееся ни разу - невозможным.
Пусть счетчик облучается потоком независимо следующих друг за другом частиц. Попадание той или иной частицы в счетчик является случайным событием. Поэтому в течение равных интервалов времени через счетчик может пролететь разное количество частиц. В этих условиях вероятность 
того, что в течение времени t в счетчик попадет n частиц, дается известной формулой Пуассона:
, (2)
где 
- среднее число актов срабатывания счетчика за время t.
Можно показать, что в случае распределения Пуассона, абсолютная погрешность 
.
По мере роста n различие между величинами вероятностей для смежных или близких n оказывается очень малым. Например, легко проверить, что при 
В этих условиях вместо вероятности осуществления того или иного числа отсчетов можно пользоваться уже другой величиной, а именно, вероятностью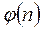 
того, что число отсчетов заключено в "бесконечно малом" интервале от n, до 
. По абсолютной величине интервал 
, может содержать несколько единиц, однако он мал по сравнению с интересующими нас n, равными по порядку величины среднему числу отсчетов 
. Тем самым дискретное распределение заменяется непрерывным. Вероятность 
распределена по закону Гаусса (
):
(3)
Из распределения Гаусса вытекает следующее: если регистрировать отсчеты счетчика в большом числе равных интервалов времени, то в 68,2% случаев число отсчетов будет отличаться от 
не более чем на 
, в 95,4% случаев отличие от будет не более чем на 
, а в 99,7% случаев число отсчетов будет отличаться от не более чем на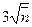 
.
Изобразить наглядно с помощью привычных графиков распределения Пуассона и Гаусса не удается, т.к. их аргументы не изменяются непрерывно. Для этой цели служит гистограмма, т.е. график в виде ступенчатой линии. Строится он так. Ось аргумента разбивается на отрезки, величина которых равна шагу изменения аргумента распределения. На каждом отрезке строится прямоугольный столбец, высота которого равна численному значению функции распределения в выбранном масштабе (рис. I.I).
Рис. I.I
