Рассмотрим систему стержневых электродов, образующих заземлитель, в однородной среде с удельным сопротивлением r. Для токов промышленной частоты можно принять, что электрическое поле является постоянным, а проводники эквипотенциальны. Линейные размеры проводников заземлителя существенно больше их поперечных размеров, так что их можно принять бесконечно тонкими.
Разделим контур заземлителя на N отрезков, расположив в середине каждого расчетную точку, как показано на рис.2.1.
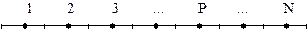
Рис.2.1
Плотность тока в пределах каждого отрезка принимается постоянной J=const. Тогда потенциал в расчетной точке P равен:
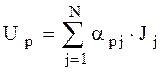, (2.1)
где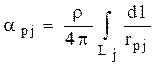 
- потенциальный коэффициент, r- удельное сопротивление земли, rpj- расстояние между расчетной точкой P и элементом интегрирования dl j-ого отрезка.
В общем случае пространственного расположения расчетной точки P и отрезка интегрирования 1-2 (рис.2.2) аналитическое вычисление интеграла при расчете взаимных потенциальных коэффициентов является затруднительным. Решение этой задачи существенно упрощается в локальной системе координат, у которой ось x совпадает, а ось y перпендикулярна направлению отрезка интегрирования, как показано на рис.2.2.
Величины h1 и h2, определяющие координаты отрезка интегрирования в новой системе, находим по известным из аналитической геометрии формулам:
,
,
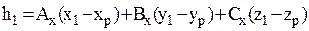где (x1,y1,z1) - координаты точки 1, (x2y2,z2)- координаты точки 2, (xp,yp,zp) - координаты расчетной точки P, (Ax,Bx,Cx) - направляющие косинусы отрезка интегрирования относительно исходной системы координат XYZ.
.
Рис 2.2.
Теперь, зная положение точки О, можно выразить направляющие косинусы новой оси y:
, 
, 
,
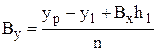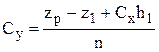где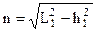 
, L1 - расстояние от точки 1 до точки P.
Потенциальный коэффициент для расчетной точки P, обусловленный током отрезка интегрирования, равен:
.
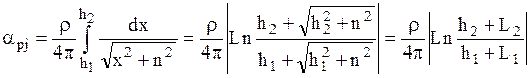Выражение для собственного потенциального коэффициента при n=R и h2=-h1=0.5h принимает вид:
,
где R- радиус стержня, h- длина отрезка интегрирования.
Найдем производные потенциального коэффициента по координатным осям:
,
.
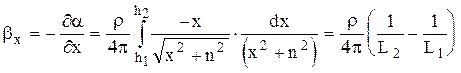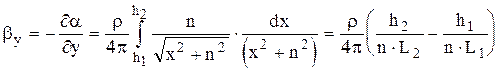В отличие от потенциальных коэффициентов, которые инвариантны к системе отсчета, коэффициенты bx,by необходимо преобразовать в реальную трехмерную систему отсчета XYZ. Для этого производится поворот координатных осей, так что
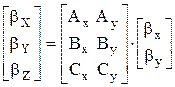, (2.2)
где A,B,C- определенные ранее направляющие косинусы координатных осей x,y относительно системы XYZ.
Рассчитав потенциальные коэффициенты, получим систему уравнений с квадратной матрицей N-ого порядка [ a ] × [ J ] = [ U ], где [ a ] - матрица коэффициентов, [ J ]- искомый вектор-столбец линейной плотности тока, [ U ]- потенциал заземлителя. Поскольку при расчете заземлителей задан полный ток, правая часть системы неизвестна. Перенесем неизвестный потенциал в левую часть системы и добавим для каждого заземлителя дополнительное условие, определяющее полный ток через токи отрезков:
,
где hi - длина отрезка с плотностью тока Ji. Для уединенного заземлителя получим систему N+1 порядка:
.
Решение системы производится стандартным методом гауссова исключения с выбором главного члена. Результатом является вектор плотности токов и потенциал заземлителя Uзаз. Сопротивление заземлителя находим как Rзаз=Uзаз/I, распределение потенциала на поверхности земли U(x,y,0) определяем по формуле (2.1), напряжение прикосновения как Uпр=Uзаз-U(x,y,0). Составляющие и модуль вектора напряженности электрического поля в любой точке пространства определяются суммированием влияния токов отрезков стержней как:
, 
, 
, 
,
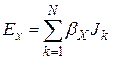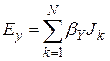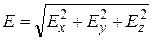где коэффициенты b определены соотношением (2.2). Плотность тока связана с напряженностью соотношением J=E/r.
