Предмет и задачи теории игр

Методические указания к проведению лекционного занятия

Тема № 9.7. Понятие об игровых моделях

План:

1. Предмет и задачи теории игр

2. Решение матричных игр в чистых стратегиях

3. Решение матричных игр в смешанных стратегиях

4. Сведение задач теории игр к задачам линейного программирования

5. Кооперативные игры

6. Игры «с природой»

Предмет и задачи теории игр

В процессе целенаправленной человеческой деятельности возникают ситуации, в которых интересы отдельных лиц (участников) либо прямо противоположны (антагонистичны), либо, не будучи непримиримыми, все же не совпадают. Примерами таких ситуаций являются спортивные игры, арбитражные споры, борьба между блоками избирателей за своих кандидатов и т. п. Здесь каждый из участников сознательно стремится добиться наилучшего результата за счет другого участника.

Подобного рода ситуации встречаются и в различных сферах производственной деятельности. Так как цели противоположны, а результат мероприятия каждой из сторон зависит от действий конкурента, то эти действия называют конфликтными ситуациями. При этом ни одна из сторон не может полностью контролировать положение, так как и той и другой стороне решения приходится принимать в условиях неопределенности. Так, при определении объема выпуска продукции на одном предприятии нельзя не учитывать размеров выпуска аналогичной продукции на других предприятиях.

В реальных условиях нередко возникают ситуации, в которых антагонизм отсутствует, но существуют противоположные тенденции. Например, для нормального функционирования производства, с одной стороны, необходимо наличие запасов разнообразных ресурсов, но с другой, – стремление к чрезвычайному увеличению этих запасов вызывает дополнительные затраты по их содержанию и хранению.

Формализованная (схематизированная) модель конфликтной ситуации называется игрой.

Раздел математики, изучающий конфликтные ситуации на основе их математических моделей, называется теорией игр.

Цель теории игр – выработка рекомендаций для различного поведения игроков в конфликтной ситуации, то есть выбор оптимальной стратегии для каждого из них.

Методы и рекомендации теории игр разрабатываются применительно к таким специфическим конфликтным ситуациям, которые обладают свойством многократной повторяемости. Если конфликтная ситуация реализуется однократно или ограниченное число раз, то рекомендации теории игр теряют смысл.

Результат игры – победа или поражение, которые не всегда имеют количественное выражение.Исход игры – это значение некоторой функции, называемой функцией выигрыша (платежной функцией), которая может задаваться либо аналитическим выражением, либо таблично (платежной матрицей).

Величина выигрыша зависит от стратегии, применяемой игроком. Стратегия – это совокупность правил, однозначно определяющих последовательность действий игрока в каждой конкретной ситуации, складывающейся в процессе игры.

Всякая игра состоит из отдельных партий. Партией называют каждый вариант реализации игры определенным образом.

В партии игроки совершают конкретные ходы. Ход – это выбор и реализация игроком одного из допустимых вариантов поведения. Ходы бывают личные (сознательные) и случайные. При личном ходе игрок самостоятельно и осознанно выбирает и реализует ту или иную чистую стратегию. Например, в шахматах каждый ход является личным.

Случайный ход – результат, получаемый не решением игрока, а каким-либо механизмом случайного выбора. Например, покупательский спрос, задержка с поставкой материалов и т. п.

Классификация игр:

- по количеству игроков;

- по количеству стратегий (конечные или бесконечные);

- в зависимости от взаимоотношений участников (бескоалиционные или некооперативные – участники не имеют права заключать соглашения, и коалиционные или кооперативные);

- по характеру выигрышей (игры с нулевой суммой – если один из игроков выигрывает ровно столько, сколько проигрывает другой и с ненулевой суммой);

- по виду функции выигрыша (матричные – (при двух участниках) выигрыши первого игрока задаются матрицей, биматричные – выигрыши каждого игрока задаются своей матрицей, непрерывные, выпуклые и др. – различаются видом аналитического выражения платежной функции);

- по количеству ходов игры (одноходовые – выигрыш распределяется после одного хода каждого игрока и многоходовые – выигрыш распределяется после нескольких ходов);

- в зависимости от объема имеющейся информации (игры с полной и неполной информацией).

Игры, в которых участники стремятся добиться для себя наилучшего результата, сознательно выбирая допустимые правилами игры способы действий, называют иногда стратегическими. Однако нередко приходится моделировать ситуации, в которых один из участников безразличен к результату игры. Такие игры называют играми с природой, понимая под термином «природа» всю совокупность внешних обстоятельств, в которых сознательному игроку (его называют иногда «лицом, принимающим решение» или «статистиком», а соответствующую игру - статистической) приходится принимать решение.

Решение матричных игр в чистых стратегиях

Для решения все возможные варианты (исходы) игры сводятся в прямоугольную таблицу – платежную матрицу, в которой строки соответствуют различным стратегиям игрока А, столбцы – стратегиям игрока В, q_ij называется ценой игры.

Для нахождения оптимальной стратегии необходимо проанализировать все возможные стратегии и рассчитывать на то, что разумный противник на каждую из них будет отвечать такой, при которой выигрыш игрока А минимален. Обычно минимальные числа в каждой строке обозначаются α_i и выписываются в виде добавочного столбца матрицы (табл.1).

Таблица 1.

В₁ В₂ … В_n α _i

А₁ q₁₁ q₁₂ … q_1n α ₁

А₂ q₂₁ q₂₂ … q_2n α ₂

… … … … … …

А_m q_m1 q_m2 … q_mn α _i

β_j β₁ β₂ … β_j

В каждой строке будет свое . Предпочтительной для игрока А является стратегия, при которой α_i обращается в максимум, то есть:

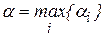или ,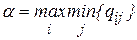

где α – максиминный выигрыш (максимин), а соответствующая ей стратегия – максиминная.

Если придерживаться максиминной стратегии, то при любом поведении стороны В (конкурента) гарантирован выигрыш, во всяком случае не меньше α. Поэтому α называют также нижней ценой игры – тот гарантированный минимум, который можно обеспечить при наиболее осторожной (перестраховочной) стратегии.

Аналогичные распределения можно провести и для конкурента В, который должен рассмотреть все свои стратегии, выделяя для каждой из них максимальные значения проигрыша:

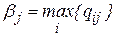(последняя строка матрицы). Из всех значений β_j находят минимальное:

,

которое дает минимаксный проигрыш или минимакс.

Такая β - стратегия — минимаксная, придерживаясь которой сторона В имеет гарантию, что в любом случае проиграет не больше β. Поэтому β называют верхней ценой игры.

Если α = β = С, то число С называют чистой ценой игры или седловой точкой.

Для игры с седловой точкой нахождение решения состоит в выборе пары максиминной и минимаксной стратегий, которые являются оптимальными, так как любое отклонение от этих стратегий приводит к уменьшению выигрыша первого игрока и увеличению проигрыша второго игрока по сравнению с ценой игры С.

Пример. Конструктор получил задание разработать определенное новое изделие. В результате исследований он определил три возможных варианта изделия У₁, У₂, У₃, каждый из которых может быть реализован каким-либо из трех техпроцессов Т₁, Т₂, Т₃.

Если первый вариант конструкции У₁ реализуется по первой технологии Т₁, то внешний вид изделия оказывается наилучшим и оценивается экспертами в 9 баллов, а при реализации по второй технологии – в 6 баллов, по третьей – в 5 баллов и т. д. (табл.2).

Таблица 2.

Матрица игры для конструктивного и технологического вариантов

Конструкция Технология

Т₁ Т₂ Т₃

У₁ У₂ У₃ 5(Т₃) 7 (Т₂ или Т₃) 5(Т₂)

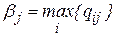
Решение.

Конфликтная ситуация возникает из-за того, что затраты на реализацию каждого конструкторско-технологического решения (варианта) не одинаковы. Для простоты полагаем, что затраты пропорциональны внешнему виду (чем выше балл, тем больше затраты).

Конструктор должен представить только один вариант – самый красивый. Но он понимает, что тогда найдутся сторонники самого дешевого варианта («экономисты»). Поэтому его задача выбрать оптимальный вариант по внешнему виду и стоимости.

Если конструктор выберет У₁, то экономисты будут настаивать на технологии Т₃. На вариант У₂ будет ответ Т₂ или Т₃ и т. д.

Очевидно, что с точки зрения конструктора преимущество имеет вариант У₂, но даже при неблагоприятных обстоятельствах получится изделие, оцениваемое в 7 баллов (выигрыш 7), а может быть даже 8, если удается уговорить экономистов на вариант Т₁.

С точки зрения экономистов в смысле снижения затрат: при выборе технологии Т₁ в варианте У₁ затраты наибольшие — 9 баллов, при Т₂ в У₂ (7), при Т₃ в У₃ (8).

То есть для экономистов оптимальным является техпроцесс Т₂, так как он требует меньших затрат при различных вариантах конструкции. Следовательно, стратегия Т₂У₂ с выигрышем 7 – наиболее выгодная сразу для обеих сторон – максимальный выигрыш У совпадает с минимальным проигрышем Т.

Важно помнить, что в матричной игре может быть несколько седловых точек. И еще: седловой элемент q_ij является наименьшим в i -ой строке и наибольшим в j -м столбце, поэтому, если игрок В отклонится от своей минимаксной стратегии, его проигрыш может только увеличиться. Аналогично, отклонение игрока А от своей максиминной стратегии ведет к уменьшению его выигрыша. Таким образом, наиболее предпочтительные стратегии в игре с седловой точкой обладают свойством устойчивости, создают ситуацию равновесия. Отсюда следует, что если в матрице игры существует седловой элемент, то наилучшими для игроков являются наиболее предпочтительные чистые стратегии.