Методи побудови планових геодезичних мереж
Планові геодезичні мережі, які функціонують нині на території України (державні, мережі згущення, спеціальні мережі), створювалися такими основними методами: тріангуляції, полігонометрії і трилатерації.
Тріангуляція — побудова на місцевості у вигляді мережі трикутників, у кожному з яких вимірюються три кути (рис. 1.1). Крім того, в деяких трикутниках вимірюються сторони, які називаються базисними. Базисних сторін в мережі має бути не менше двох. На основі першої з використанням теореми синусів обчислюються довжини усіх інших сторін. Друга та наступна базисні сторони служать для контролю обчислень. На кінцях базисних сторін виконують астрономічні спостереження, з яких знаходять координати вихідних пунктів та азимути (а потім дирекційні кути) базисних сторін. Дирекційні кути інших сторін знаходять з обчислень. На основі довжин сторін і їх дирекційних кутів знаходять приростки координат по кожній стороні і координати усіх пунктів тріангуляції.
Рисунок 1.1 - Мережа тріангуляції
Полігонометрія — побудова на місцевості у вигляді системи ламаних ліній, у яких вимірюються сторони і кути при вершинах (рис. 1.2). Полігонометричні ходи опираються на вихідні сторони АВ і СD. На початку А і в кінці С ходу виконують астрономічні спостереження, з яких визначають координати цих пунктів та азимути, а потім дирекційні кути вихідних сторін АВ і СD.
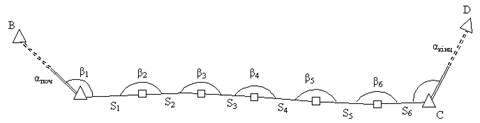
Рисунок 1.2 - Мережа полігонометрії
Трилатерація — побудова на місцевості у вигляді мережі трикутників, у яких вимірюються три сторони (рис. 1.3).
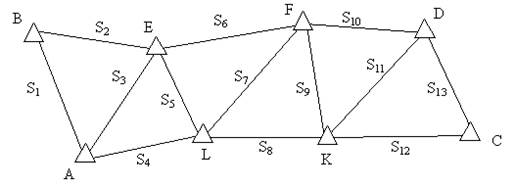
Рисинок 1.3 - Мережа трилатерації
Мережі трикутників повинні опиратися на дві або більше вихідні сторони. На одному кінці кожної з цих сторін виконуються астрономічні спостереження, з яких визначають координати вихідних пунктів та азимути (дирекційні кути) вихідних сторін.
В останні десятиріччя в зв’язку з швидким розвитком супутникової геодезії при оновленні та реконструкції планової ДГМ, згідно з “Основними положеннями створення державної геодезичної мережі України” 1998р. [4] у геодезичне виробництво широко впроваджено новий метод створення геодезичних мереж з використанням супутникових радіонавігаційних систем GPS (Global Position Station). В цьому методі положення кожного пункту геодезичної мережі визначається незалежно від інших пунктів мережі за результатами спостережень штучних супутників Землі.
1.1.2 Схема планових мереж, побудованих згідно з “Основними положеннями 1954–1961 рр.”
На сьогоднішній день на території України функціонує державна геодезична мережа, яка є складовою частиною державної геодезичної мережі СРСР, що була побудована на протязі 50–90 років XX століття. Ця мережа є однією з найбільш унікальних за розмірами і точністю мереж у світі. Основні принципи побудови геодезичної мережі були викладені в 1961 р. в “Основних положеннях про побудову державної геодезичної мережі СРСР”, які пізніше отримали скорочену назву “Основні положення 1954–1961 рр.”
Згідно з цим документом, планова державна геодезична мережа СРСР поділялася на чотири класи: 1, 2, 3, 4-й.
Спочатку будувалася астрономо–геодезична мережа 1 і 2 класу. Астрономо-геодезична мережа 1 класу будувалася у вигляді полігонів периметром 800–1000 км. Полігони утворювалися ланками тріангуляції або полігонометрії довжиною не більше 200 км (рис 1.4).
На кінцях ланок будувалися два пункти Лапласа, на яких виконувалися астрономічні визначення довгот, широт та геодезичних азимутів базисних сторін. Ряди тріангуляції складалися з трикутників, близьких до рівносторонніх, або з геодезичних чотирикутників. Геодезичний чотирикутник — це чотирикутник з двома діагоналями. Довжини сторін в трикутниках або геодезичних чотирикутниках 20–25 км. Ряди тріангуляції могли бути замінені рядами полігонометрії з довжинами сторін 20–25 км.
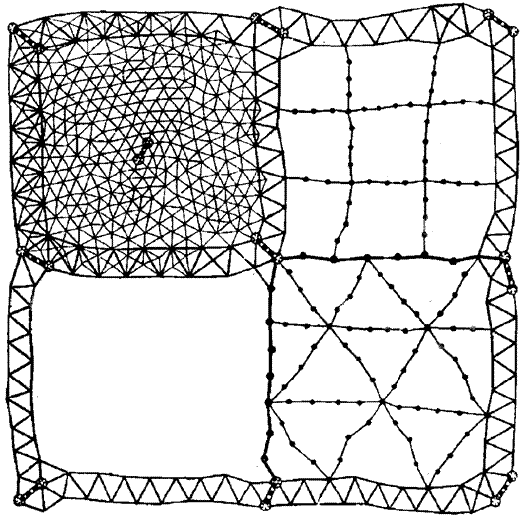
| Базисна сторона і пункт Лапласа |
| Тріангуляція 1 класу |
| Тріангуляція 2 класу |
| Полігонометрія 1 класу |
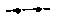
| Полігонометрія 2 класу |
Рисунок 1.4 - Схема планової ДГМ, побудованої згідно з
”Основними положеннями 1954–1961 рр.”
Астрономо-геодезична мережа 2 класу будувалася у вигляді суцільної мережі трикутників, розміщених між вихідними базисами. Довжини сторін трикутників 7–20 км. В суцільній мережі не рідше, ніж через 25 трикутників, вимірювалися базисні сторони, на кінцях яких встановлювалися пункти Лапласа, для яких визначалися астрономічними методами довготи, широти і геодезичні азимути базисних сторін. Мережі 2 класу будувалися також у вигляді полігонометрії (рис. 1.4), в основному метод полігонометрії знаходив своє застосування в залісених районах. Були спроби використання при створенні мереж 2 класу методу трилатерації, але вони не дали належних за точністю результатів.
Мережі тріангуляції 3 класу будувалися у вигляді вставок у трикутники вищого класу (рис. 1.5), або у вигляді жорстких систем (рис. 1.6).
| 
|
| Рисунок 1.5 - Вставка у трикутник вищого класу | Рисунок 1.6 - Жорстка система |
Жорстка система являє собою систему з п'яти і більше пунктів, в якій пункти 3 класу з’єднувалися між собою і з пунктами вищого класу. Довжини сторін 3 класу — 5–8 км.
Подібно до 3 класу будувалися мережі тріангуляції 4 класу: у вигляді вставок у трикутники вищого класу та у вигляді жорстких систем. Довжини сторін 4 класу становили 2–5 км.
Метод полігонометрії при створенні мереж 3 і 4 класу також знайшов широке застосування. Ці мережі за точністю нічим не поступалися перед мережами тріангуляції.
Що стосується методу трилатерації, то він отримав застосування лише при побудові мереж 3 і 4 класів, проте ці мережі за точністю поступалися мережам, створеним методами тріангуляції та полігонометрії.
Нижче приведені основні технічні характеристики державних мереж, побудованих згідно з “Основними положеннями 1954–1961 рр.” методом тріангуляції (табл. 1.1) і методом полігонометрії (табл. 1.2).
Оскільки для забезпечення топографічних знімань державних мереж було недостатньо, їх подальше згущення здійснювалося мережами 1 і 2 розрядів, які створювалися такими ж методами, що і державні мережі.
Таблиця 1.1 - Основні технічні характеристики державних мереж тріангуляції, побудованих згідно з “Основними положеннями 1954 –1961 рр.”
| Назва показника | Клас тріангуляції | |||
| Середня довжина сторони, км | 20–25 | 7–20 | 5–8 | 2–5 |
| Відносна помилка базисної (вихідної) сторони (m b/ b) | 1:400000 | 1:300000 | 1:200000 | 1:200000 |
| Відносна помилка сторони в слабкому місці (m s/ s) | 1:150000 | 1:200000 | 1:120000 | 1:70000 |
| Допустима нев’язка трикутника | 3″ | 4″ | 6″ | 8″ |
| Сер. кв. помилка вимірювання кута (за нев'язками трикутників) | 0.″7 | 1″ | 1.″5 | 2″ |
| Сер. кв. помилка астрономічних визначень: широти довготи азимута | 0.″3 0.03 0.″5 | 0.″3 0.03 0.″5 | — — — | — — — |
Таблиця 1.2 - Основні технічні характеристики державних мереж полігонометрії, побудованих згідно з “Основними положеннями 1954 –1961 рр.”
| Назва показника | Клас полігонометрії | |||
| Довжина ходу, км Довжина сторони, км | 20–25 | за спеціально розробленою програмою | — не менше 3 | 0.25–2 |
| Сер. кв. помилка вимірювання кутів | 0.″4 | 1″ | 1.″5 | 2″ |
| Відносна помилка вимірювання сторін | 1:300000 | 1:250000 | 1:200000 | — |
| Кількість сторін в ході, не більше | — | — |
1.1.3 Характеристика сучасної планової геодезичної мережі України
В зв’язку з науково-технічним прогресом, який відбувається у світі, і новими завданнями, які ставляться перед геодезичною галуззю України, державна геодезична мережа, підлягає оновленню та модернізації. 8 червня 1998р. постановою Кабінету Міністрів України затверджені “Основні положення створення державної геодезичної мережі України”. В 1999 році Головним Управлінням Геодезії Картографії та Кадастру при Кабінеті Міністрів України видана “Інструкція з топографічного знімання у масштабах 1:5000, 1:2000, 1:1000 та 1:500”
Згідно з цими документами, планова геодезична мережа України складається з державної мережі (астрономо-геодезична мережа 1 класу, геодезична мережа 2 класу, геодезична мережа 3 класу), мережі згущення
(4 класу, 1 і 2 розрядів) та знімальної мережі.
Перш ніж давати характеристику цих мереж, розглянемо питання їх щільності.
1.1.3.1 Щільність геодезичних пунктів
Введемо поняття щільності геодезичних пунктів.
Під щільністю геодезичних пунктів розуміють площу території, яка забезпечується одним пунктом. Чим менша ця площа, тим більшою є щільність. Нормативні документи встановлюють необхідну щільність пунктів. При її обґрунтуванні береться до уваги масштаб і призначення майбутніх топографічних знімань.
Так, у відповідності до “Інструкції з топографічного знімання у масштабах 1:5000, 1:2000, 1:1000, 1:500” Київ, ГУГКіК, 1999, середня щільність пунктів планової державної геодезичної мережі для створення геодезичної основи топографічних знімань на незабудованих територіях в масштабі 1:5000 повинна бути доведена до одного пункту на 20–30 км2 і в масштабі 1:2000 — до одного пункту на 5–15 км2 (п. 1.1.24). На забудованих територіях щільність пунктів ДГМ повинна бути доведена до одного пункту на 5 км2.
Щільність планових геодезичних мереж згущення поза населеними пунктами повинна бути доведена до одного пункту на 7–10 км2 для знімань у масштабі 1:5000, і до одного пункту на 2 км2 для знімань у масштабі 1:2000.
У містах, селищах та інших населених пунктах, а також на промислових майданчиках щільність мереж згущення має бути один пункт на 1 км2 на незабудованих територіях та чотири пункти на 1 км2 — у забудованих частинах.
1.1.3.2 Характеристика астрономо-геодезичної мережі 1 класу
Астрономо-геодезична мережа 1 класу (АГМ-1) будується у вигляді однорідної за точністю просторової геодезичної мережі, яка складається з рівномірно розміщених геодезичних пунктів, віддалених один від одного
на 50–150 км.
АГМ-1 є геодезичною основою для побудови нових геодезичних мереж і забезпечення подальшого підвищення точності існуючої ДГМ з використанням методів супутникової геодезії.
Частина пунктів АГМ-1 являє собою постійно діючі пункти GPS спостережень та астрономо-геодезичні обсерваторії, на яких виконується комплекс супутникових астрономо-геодезичних, гравіметричних та геофізичних спостережень, що забезпечують безперервне відтворення загальної геодезичної системи координат.
Решта пунктів АГМ-1 — це фундаментально закріплені на місцевості пункти, положення яких періодично визначається в рамках довгострокової програми функціонування ДГМ.
Система координат, яка задається пунктами АГМ-1, узгоджується з фундаментальними астрономічними (небесними) системами координат і надійно зв’язана з аналогічними системами різних держав у рамках узгодження наукових проектів міжнародного співробітництва.
Кожний пункт АГМ-1 повинен бути зв’язаний GPS-вимірюваннями не менше, як з трьома суміжними пунктами мережі.
Пункти АГМ-1 повинні бути вставлені в мережу високоточного нівелювання, що дозволяє визначити перевищення нормальних висот між суміжними пунктами АГМ-1 з середньоквадратичними помилками не більше 0,05 метра.
На кожному пункті АГМ-1 виконуються і періодично повторюються визначення відхилень вискових ліній з середньоквадратичною помилкою 0,5”.
Кількість пунктів АГМ-1 та їх розташування визначається програмою побудови ДГМ.
1.1.3.3 Основні вимоги до побудови геодезичної мережі 2 класу
Геодезична мережа 2 класу будується у вигляді однорідної за точністю просторової геодезичної мережі, яка складається з рівномірно розміщених геодезичних пунктів існуючої геодезичної мережі 1 та 2 класів, побудованих згідно з вимогами “Основних положень 1954 – 1961 рр.” і нових пунктів, що визначаються відповідно до вимог цих “Основних положень”.
Геодезична мережа 2 класу є вихідною геодезичною основою для побудови геодезичної мережі згущення 3 класу та геодезичних мереж спеціального призначення з використанням методів супутникової геодезії та традиційних геодезичних методів.
Нові пункти геодезичної мережі 2 класу розміщуються на відстані
8–12 км один від одного, а на території міських населених пунктів, великих промислових об'єктів — 5–8 км, їх положення визначається, як правило, відносними методами супутникової геодезії, а також традиційними геодезичними методами (тріангуляції, трилатерації, полігонометрії), які забезпечують точність визначення взаємного положення пунктів з середньоквадратичними помилками величиною 0,03–0,05 метра при середній довжині сторін 10 кілометрів.
За вихідні пункти для визначення координат пунктів геодезичної мережі 2 класу приймаються пункти АГМ-1. Група нових пунктів геодезичної мережі 2 класу, що визначаються, повинна мати зв’язок не менше, ніж з трьома пунктами АГМ-1.
Основні вимоги до побудови геодезичної мережі 2 класу наведено в таблиці 1.3.
Висоти марок верхніх пунктів геодезичної мережі 2 класу повинні визначатися геометричним нівелюванням, яке забезпечує точність взаємного положення пунктів за висотою з середньоквадратичною помилкою не більшою 0,05 метра. В гірській і важко доступній місцевості нормальні висоти можуть визначатися тригонометричним нівелюванням або GPS-нівелюванням, яке виконується методами супутникової геодезії. У цьому випадку СКП визначення взаємного положення суміжних пунктів за висотою не повинна перевищувати 0,20 метра.
Таблиця 1.3 - Основні вимоги до побудови геодезичної мережі 2 класу
| Параметри мережі | Метод побудови | |||
| GPS | тріангу- ляція | полігоно-мерія | трилатерація | |
| Периметр полігона, км Найбільша довжина ходу, км | 150–180 | |||
| Довжина сторони, (віддаль між пунктами в GPS), км Найбільша Найменша | ||||
| Кількість сторін у ході не більше | ||||
| Сер. квадр.помилка взаємного положення пунктів, м | 0,03–0,05 | 0,03–0,05 | 0,03–0,05 | 0,03–0,05 |
| Сер. квадр.помилка вимірювання кутів не більше, кутові сек. | 1″ | 1″ | ||
| Найбільша нев’язка трикутника | 4″ | |||
| Кутова нев’язка ходу, сек | 2″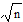 
| |||
| Відносна помилка вимірювання вихідної сторони (базису) не більше, m s/s | 1:300000 | 1:300000 | ||
| Сер.квадр.помилка вимірювання сторони не більше, м | 0,03 | 0,03 |
1.1.3.4 Основні вимоги до побудови геодезичної мережі 3 класу
Геодезична мережа 3 класу будується з метою збільшення кількості пунктів до щільності, яка забезпечує створення знімальної основи великомасштабних топографічних та кадастрових зйомок. Вона включає геодезичні мережі 3 та 4 класів, які побудовані згідно з вимогами “Основних положень 1954–1961 рр.”, та нові мережі 3 класу, що визначаються згідно з вимогами цих “Основних положень”.
Нові пункти геодезичної мережі 3 класу визначаються відносними методами супутникової геодезії, а також традиційними геодезичними методами полігонометрії, тріангуляції та трилатерації. При цьому середньоквадратична помилка визначення взаємного положення пунктів в плані повинна бути не більшою 0,05 метра.
Вихідними пунктами для побудови геодезичної мережі 3 класу служать пункти астрономо-геодезичної мережі 1 класу і геодезичної мережі 2 класу.
У геодезичній мережі 3 класу за можливістю повинна забезпечуватись видимість (земля-земля) між суміжними пунктами мережі, а в разі її відсутності на пункті закладається два орієнтирних пункти згідно з вимогами цих “Основних положень”.
Під час визначення пунктів геодезичної мережі 3 класу методом полігонометрії прокладаються окремі ходи або системи з вузловими точками, які опираються на пункти більш високого класу.
Якщо відстань між пунктами, що належить до різних ходів, менше 2 км, здійснюється взаємний зв’язок таких ходів.
Основні вимоги до побудови геодезичної мережі 3 класу наведено в таблиці 1.4.
Характеристика сучасних планових мереж згущення
Державних планових геодезичних мереж недостатньо для забезпечення топографічних знімань усіх масштабів. З цією метою державні геодезичні мережі згущують пунктами 4 класу, а в разі необхідності, пунктами 1 і 2 розрядів, які відносяться до мереж згущення. Для їх створення застосовують ті ж відомі методи: тріангуляції, полігонометрії, трилатерації, а також віддавна відомі методи засічок або сучасні методи GPS.
Таблиця 1.4 - Основні вимоги до побудови геодезичної мережі 3 класу
| Параметри мережі | Методи побудови | |||
| GPS | тріан-гуляція | полігоно-метрія | Трилате-рація | |
| Периметр полігону, км | 70–90 | |||
| Найбільша довжина ходу, км | ||||
| Довжина сторони (віддаль між пунктами GPS), км Найбільша Найменша | ||||
| Кількість сторін в ході не більше | ||||
| Сер. кв. помилка взаємного положення пунктів, м | 0,05 | 0,05 | 0,05 | 0,05 |
| Сер. кв. помилка вимірювання кутів не більше, кутові сек. | 1″,5 | 1″,5 | ||
| Найбільша нев’язка трикутника, сек. | 6″ | |||
| Кутова нев’язка ходу, сек. | 3″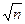 
| |||
| Відносна помилка вимірювання вихідної сторони (базису) не більше, ms/s | 1:200000 | 1:200000 | ||
| Сер. кв. помилка вимірювання сторони не більше, м | 0,04 | 0,04 |
При створенні мереж згущення методом тріангуляції необхідно дотримуватись вимог, поданих у таблиці 1.5.
При створенні мереж згущення методом трилатерації необхідно дотримуватись вимог, поданих у таблиці 1.6.
При створенні мереж згущення методом полігонометрії необхідно дотримуватись вимог, поданих у таблиці 1.7.
При створенні мереж згущення методом GPS необхідно дотримуватись вимог, поданих у таблиці 1.8.
Таблиця 1.5 - Основні вимоги до побудови планових мереж згущення методом тріангуляції
| Показники | 4 клас | 1 розряд | 2 розряд |
| Довжина сторони трикутника, км, не більше | 5,0 | 5,0 | 3,0 |
| Мінімально допустима величина кута, кутові градуси: | |||
| у суцільній мережі | |||
| сполучного в ланцюжку трикутників | |||
| у вставці | |||
| Кількість трикутників між вихідними сторонами або між вихідним пунктом і вихідною стороною, не більше | |||
| Мінімальна довжина вихідної сторони, км | |||
| Граничне значення середньої квадратичної помилки кута, що обчислена за нев'язкими у трикутниках, кутові секунди | |||
| Гранично допустима нев'язка в трикутнику, кутові секунди | |||
| Відносна помилка вихідної (базисної) сторони, не більше | 1:200000 | 1:50000 | 1:20000 |
| Відносна помилка визначення довжини сторони в найбільш слабкому місці, не більше | 1:50000 | 1:20000 | 1:10000 |
Таблиця 1.6 - Основні вимоги до побудови планових мереж згущення методом трилатерації
| Показники | 4 клас | 1 розряд | 2 розряд |
| Довжина сторони трикутника, км | 2–5 | 0,5–5 | 0,25–3 |
| Мінімально допустима величина кута трикутника | 30º | 20º | 20º |
| Кількість трикутників між вихідними сторонами або між вихідним пунктом і вихідною стороною | — | ||
| Мінімальна довжина вихідної сторони, км | |||
| Відносна середня квадратична помилка вимірювання сторони мережі | 1/40000 | 1/20000 | 1/10000 |
Таблиця 1.7 - Основні вимоги до побудови планових мереж згущення методом полігонометрії
| Показники | 4 клас | 1 розряд | 2 розряд |
| Гранична довжина ходу, км: окремого між вихідною і вузловою точками між вузловими точками | 14,0 9,0 7,0 | 7,0 5,0 4,0 | 4,0 3,0 2,0 |
| Граничний периметр полігону, км | |||
| Максимальна довжина сторони ходу, км | 3,0 | 0,80 | 0,50 |
| Мінімальна довжина сторони ходу, км | 0,25 | 0,12 | 0,08 |
| Середні довжини сторін ходу, км | 0,50 | 0,30 | 0,20 |
| Кількість сторін у ході, не більше | |||
| Відносна помилка ходу, не більше | 1:25000 | 1:10000 | 1:5000 |
Продовження таблиці 1.7
| Середня квадратична помилка виміряного кута (за нев’язками у ходах і в полігонах), кутові секунди, не більше | 3″ | 5″ | 10″ |
| Кутова нев’язка ходу або полігона, кутові секунди, не більше (n +1 — кількість кутів у ході) |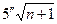 
| 
| 
|
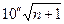
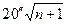
| Середня квадратична помилка вимірювання довжини сторони, см: до 500 м від 500 м до 1000 м більше 1000 м | 1:40000 | — | — — |
Таблиця 1.8 - Основні вимоги до побудови планових мереж згущення методом GPS
| Частота | Довжина бази, км | Кількість супутників | Тривалість сесії, хв. | Точність визначення (10-6 D) мм |
| Одна | Статистичне знімання | |||
| 5–10 | ||||
| Кінематичне знімання | ||||
| Одна Дві (Р-код) | 0,1 0,1 |
2 СТВОРЕННЯ ПЛАНОВИХ ГЕОДЕЗИЧНИХ МЕРЕЖ МЕТОДОМ ТРІАНГУЛЯЦІЇ
Комплекс робіт при побудові планових геодезичних мереж методом тріангуляції складається з таких процесів:
- проектні роботи;
- рекогностування пунктів тріангуляції;
- закладання центрів та будівництво зовнішніх знаків;
- астрономічні спостереження на вихідних пунктах;
- вимірювання базисів або вихідних сторін;
- кутові спостереження на пунктах тріангуляції і їх попередня обробка;
- вимірювання зенітних відстаней і їх попередня обробка;
- вирівнювальні обчислення в тріангуляції;
- вирівнювальні обчислення в тригонометричному нівелюванні.
2.1 Проектні роботи
Проектування — один з найвідповідальніших процесів великого комплексу тріангуляційних робіт. Від якості проектних робіт залежить велика частина успіху усієї роботи. Виконують проектні роботи найдосвідченіші спеціалісти геодезичного виробництва.
Проектні роботи полягають в складанні документу, який називається технічним проектом на виробництво робіт. Як правило, технічний проект складає та організація, яка буде виконувати роботи.
Технічний проект складають в такій послідовності. Спочатку висвітлюються такі питання: мета робіт, які проектуються, адміністративне розміщення об’єкту, фізико-географічний огляд і економічна характеристика об’єкту, топографо-геодезична вивченість об’єкту. Потім розробляється проект мережі на карті, який супроводжується необхідними техніко-економічними розрахунками, пізніше висвітлюється технологія та організація польового і камерального виробництва і складається кошторис на виконання робіт (кошторис — документ, в якому представлені всі витрати на виконання польових і камеральних робіт на об’єкті).
Зупинимося на питаннях проектування тріангуляційних мереж на топографічній карті, яке супроводжується розрахунком висот тріангуляційних знаків.
2.1.1 Проектування тріангуляційних мереж на топографічній карті
Проектувати державні мережі тріангуляції 2 класу найкраще на картах масштабу 1:100000. При проектуванні дотримуються основних вимог до побудови геодезичних мереж, якими є: а) запроектована мережа тріангуляції
2 класу повинна мати зв’язок не менше, ніж з трьома пунктами астрономо-геодезичної мережі 1 класу (АГМ-1), яка побудована з використанням систем GPS; б) довжини сторін в тріангуляції 2 класу повинні лежати в межах 7–20 км (див. табл. 1.3).
Проектування розпочинають з нанесення на карту існуючих на даному об’єкті або поблизу нього пунктів АГМ-1. Пункти тріангуляції 2 класу проектують у вигляді суцільної мережі близьких до правильних трикутників з довжинами сторін від 7 до 20 км. Пункти розміщують на командних висотах, щоб забезпечити видимість між ними. Якщо рельєф місцевості не дозволяє побудувати трикутники близькі до правильних, дозволяється будувати різносторонні трикутники, але кути в них повинні бути меншими 30º.
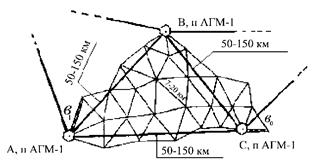
Рисунок 2.1 - Зв’язок мережі тріангуляції 2 класу з пунктами АГМ-1
Для зв’язку з пунктами АГМ-1 можуть застосовуватись різні схеми, але найдоцільнішим є безпосереднє примикання мережі 2 класу до пунктів АГМ-1, з допомогою яких буде здійснено орієнтування мережі 2 класу відносно осьового меридіану (рис. 2.1). Для масштабування мережі необхідно не менш ніж на двох її сторонах запроектувати світловіддалемірні вимірювання. Ці сторони називають базисними. Їх розміщують не рідше ніж через 25 трикутників мережі.
Для проектування державних мереж 3 класу можна використати як карти масштабу 1:100000, так і карти масштабу 1:50000. При проектуванні дотримуються вимог таблиці 1.4. Довжини сторін мережі 3 класу повинні лежати в межах 5–8 км. Пункти 3 класу проектуються у вигляді вставок у трикутники вищого класу або у вигляді жорстких систем, про які згадувалося у п. 1.1.2 (див. рис. 1.5 і 1.6).
Для проектування мереж згущення (4 класу, 1 і 2 розряду) використовують топографічні карти масштабів 1:25000 і 1:10000. Мережі згущення будуються у вигляді вставок у трикутники вищого класу або у вигляді жорстких систем (див. рис. 1.5 і 1.6), а також у вигляді рядів тріангуляції (рис. 2.7).
2.1.2 Розрахунок висот зовнішніх знаків
Між суміжними пунктами планової геодезичної мережі, яка будується методом тріангуляції, має бути взаємна видимість. Якщо цього не вдається досягнути безпосередньо з землі, на пунктах будують зовнішні знаки у вигляді пірамід або у вигляді сигналів. Піраміда — це дерев’яна або металічна споруда, на якій закріплюється візирний циліндр, що служить візирною ціллю для спостережень з інших пунктів тріангуляції. Сигнал — це дерев’яна або металічна споруда, на якій крім візирного циліндра, встановлюється столик для приладу (теодоліта, світловіддалеміра чи відбивача). Висоти зовнішніх знаків повинні бути такими, щоб забезпечувалась видимість між пунктами при спостереженнях, і в той же час оптимальними (достатніми, але не надмірними). Їх визначають заздалегідь при проектуванні.
2.1.2.1 Теоретичне обґрунтування розрахунку висот знаків
Щоб правильно визначити висоту зовнішніх знаків, які мають забезпечити видимість між двома пунктами тріангуляції, необхідно врахувати вплив таких факторів:
а) кривизни Землі;
б) вертикальної рефракції;
в) висоти перешкоди.
На рис. 2.2 точки А і В — пункти тріангуляції, НA і НB — їх висоти над рівнем моря, які показані відрізками по нормалях між геоїдом і рівневими поверхнями, що проходять через точки А і В.
С — вершина перешкоди (на рис.2.2 — вершина лісу на горі).
НC — висота вершини перешкоди над рівнем моря.
Позначимо hA = НC – НA, hB = НC – НB — перевищення вершини перешкоди над основами знаків А і В.
Для того, щоб забезпечити видимість між пунктами А і В, в пункті А необхідно побудувати сигнал висотою LA = АА", в пункті В — висотою LB = ВВ".
З рис. 2.2 видно, що
| LA = hA + VA, | (2.1) |
де VA=VA ′- VA ″
| LB = hB + VB, | (2.2) |
де VB=VB ′- VB ″
де VA і V B — поправки за кривизну Землі і вертикальну рефракцію для пунктів А і В відповідно. Перевищення ha і hв легко знаходяться за допомогою висот пунктів А і В, знятих з карти, і висоти вершини перешкоди С, яка дорівнює висоті земної поверхні, знятій з карти, плюс висота лісу чи споруди над поверхнею Землі.
Рисунок 2.2 - Врахування впливу кривизни Землі, вертикальної рефракції і висоти перешкоди на висоти тріангуляційних знаків
Обґрунтування впливу кривизни Землі покажемо з допомогою рис. 2.3.
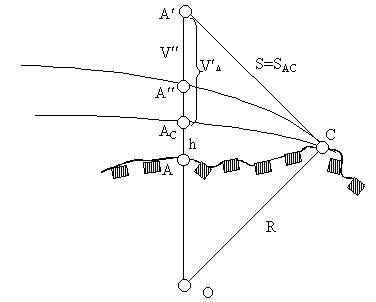
Рисунок 2.3 - Вплив кривизни Землі на висоту сигналу
Точка С — вершина перешкоди, точка Ас — точка в пункті А, піднята на рівневу поверхню, яка проходить через точку С. СА ′ — дотична до дуги САс в точці С, вона являє собою пряму, по якій проходить горизонтальний світловий промінь. Щоб в точці А ′ побачити точку С, там треба піднятися на висоту V ′ A=АсА ′. Розглянемо прямокутний трикутник ОА'С, в ньому ОС = R — радіус Землі, А'С=SAC — віддаль між пунктом тріангуляції А і перешкодою С. Тоді:
 .
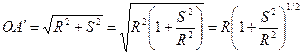| (2.3) |
Член в дужках розкладемо за біномом Ньютона: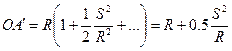 
. Оскільки ОАс=R, то АсА ′ =ОА ′ –R=0.5S2/R.
Раніше ми позначали АсА ′ =VA ′. Це буде висота зовнішнього знаку, який треба побудувати в точці Ас, щоб врахувати кривизну Землі при забезпеченні видимості між пунктами А і С.
Отже:
 .
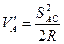| (2.4) |
Але візирний промінь від т. С буде проходити не по прямій СА ′, а буде заломлюватися внаслідок зміни густини повітря на своєму шляху, яка в свою чергу змінюється від зміни метеорологічних параметрів (температури, вологості, тиску). Це явище носить назву рефракції. Заломлення променя буде відбуватись по кривій, яка має подвійну кривизну у просторі. Цю криву можна розкласти на дві: одну — в горизонтальній площині, другу — у вертикальній. Заломлення променів в горизонтальній площині назвемо горизонтальною рефракцією, у вертикальній — вертикальною рефракцією. В даному випадку маємо справу з вертикальною рефракцією. Встановлено, що крива СА" по якій проходить промінь за рахунок вертикальної рефракції, своєю вигнутістю направлена до Землі, вона має приблизно таку ж природу, що і кривизна Землі, з тією лише різницею, що її вплив на висоту знака буде здійснюватися з коефіцієнтом k, який називається коефіцієнтом вертикальної рефракції, причому цей вплив приводить до зменшення висоти знака на величину А ′ А"=VA", де:
 .
| (2.5) |
Сумарний вплив кривизни Землі і вертикальної рефракції:
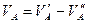
| (2.6) |
або:
 .
| (2.7) |
З досліджень встановлено, що к в середньому дорівнює 0,14–0,16.
Якщо за середній радіус Землі взяти R =6373 км, а за середній коефіцієнт вертикальної рефракції k =0,15,то отримаємо таку величину впливу кривизни Землі і вертикальної рефракції(в км):
.
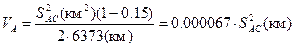Після переведення в метри
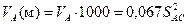
або
 ,
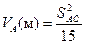| (2.8) |
де SAC — довжина сторони між пунктами А і С в кілометрах.
Аналогічно можемо отримати величину впливу кривизни Землі і вертикальної рефракції для пункту В
 .
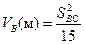| (2.9) |
Підставивши (2.8) і (2.9) у формули (2.1) і (2.2) відповідно, отримаємо:
 ,
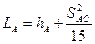| (2.10) |
 .
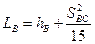| (2.11) |
За цими формулами виконують аналітичний розрахунок висот знаків на пунктах А і В.
2.1.2.2 Коректування висот знаків за правилом коромисла
Запроектовані висоти знаків на пунктах тріангуляції повинні, по-перше, забезпечувати видимість між пунктами, а по-друге, бути оптимальними. Оптимальними вважають висоти знаків, якщо їх сума є мінімальною. Тому проектування виконують в кількох варіантах, з яких вибирають оптимальний. Часто при аналізі варіантів доводиться на одному з пунктів змінювати висоту знаку, що призводить до зміни висот сигналів на інших пунктах, суміжних з даним. Цю зміну можна визначити за правилом коромисла, а саме: якщо на пункті А збільшити висоту знаку на величину Δ Н 1, то на пункті В висоту знаку необхідно зменшити на висоту
 ,
| (2.12) |
де S 1 і S2 — віддалі до перешкоди від пунктів А і В відповідно (рис.2.4).
Цим правилом вигідно коректувати висоти знаків у випадку, коли S 2 більша за S 1 в 2–3 рази, тоді висота знака на пункті В зменшиться на величину в 2–3 рази більшу тієї, на яку збільшується висота знака на пункті А. В результаті — зменшення суми висот знаків на стороні АВ.
Рисунок 2.4 - Правило коромисла
На рисунку:
L 1 — початкова висота знаку в т. А,
∆ H 1 — величина, на яку необхідно збільшити висоту знаку в т. А,
L´ 1 — скоректована висота знаку в т. А,
L 2 — початкова висота знаку в т. В,
∆ H 2 — величина, на яку необхідно зменшити висоту знаку в т. В
L´ 2 — скоректована висота знаку в т. В.
2.1.2.3 Графічний розрахунок висот знаків
Графічний розрахунок висот знаків виконується на міліметровому папері. На горизонтальній осі в масштабі карти відкладають віддалі SАС і SВС перешкоди С до пунктів А і В і під віссю підписують відмітки біля основи знака і біля вершини перешкоди. Горизонтальній осі присвоюють умовну відмітку, яка повинна бути на 5–10 м меншою підписаних відміток під точками А, В і С (рис. 2.5).
На вертикальних лініях в масштабі 1:1000 відкладають відмітки НС,
НА–V 1 і НВ–V2, де V 1 і V2 — поправки за кривизну Землі і вертикальну рефракцію, які обчислюються за формулами 2.8. і 2.9.
Рисунок 2.5 - Графічний розрахунок висот знаків
Масштаби: горизонтальний 1:50 000, вертикальний 1:1 000
Отримують точки А ′, С' і В ′. Вони являють собою зображення основ знаків А і В на землі і вершини перешкоди, яка може лежати як на землі, так і на якійсь висоті над землею (наприклад, вершина лісу).
Дотикаючись точки С' лінійкою, проводять лінію А"В". Відрізки А'А" і В'В" являють собою висоти знаків LA, LB. З багатьох варіантів лінію А"В" намагаються провести так, щоб сума висот знаків LA і Lв була мінімальною. Запроектовані знаки наносять на міліметровий папір чорним кольором і підписують їх висоту. Тут під висотою знака розуміють віддаль по вертикалі від центра пункту до столика під прилад.
Якщо визначення в результаті розрахунку висоти менші 1,5 м (висота штативу на землі), на пункті проектують піраміду. Намагаються не проектувати сигнали, якщо отримані висоти лежать в межах 1,5–4 м. В цьому випадку коректують висоти знаків, зменшивши на даному пункті висоту до нуля і збільшивши висоту знака на протилежному кінці лінії. Але в цьому випадку, можливо, необхідно буде підкоректувати висоти знаків на інших суміжних пунктах.
Якщо на одному з пунктів, наприклад, А, існує знак або його запроектовано раніше (для мережі вищого класу), його висоту LA слід нанести в вертикальному масштабі червоним кольором. Лінію A''B'' в цьому випадку проводять з врахуванням висоти LA. При розрахунку висот знаків можуть виникнути інші ситуації, до вирішення яких необхідно підходити з точки зору зменшення вартості будівельних робіт.
2.1.3 Оцінка проектів тріангуляційних мереж
2.1.3.1 Суть та призначення оцінки проектів тріангуляційних мереж
Запроектовані на карті мережі підлягають попередній оцінці, метою якої є встановити, з якою точністю можна отримати основні параметри мережі (координати пунктів, довжини та дирекційні кути сторін тощо). Як відомо, ці параметри залежать від вихідних даних, точності польових вимірів, розмірів та конфігурації мережі. Після оцінки проекту ми маємо отримати відповідь на запитання: чи запроектована мережа даних розмірів та конфігурації при дотриманні необхідної точності польових вимірів буде відповідати необхідним технічним вимогам чи ні. Якщо буде, проект можна реалізувати в практику, якщо ні, необхідно запропонувати інший варіант мережі.
Оцінку проектів виконують строгими або наближеними методами. Строгі методи здійснюються за тими ж алгоритмами, які передбачено використовувати при вирівнюванні мереж. Вони досить трудомісткі, вимагають уважного складання умовних рівнянь або рівнянь поправок для мережі. Строгі методи оцінки проектів вивчаються в спеціальному курсі “Математична обробка геодезичних вимірів”.
Тут ми зупинимося на кількох наближених методах оцінки проектів, які можна застосовувати для державних тріангуляційних мереж 3 класу, а також мереж згущення 4 класу, 1 і 2 розряду.
Вставка в трикутник вищого класу
Вставка в трикутник вищого класу показана на рис. 2.6.
Рисунок 2.6 - Вставка в трикутник вищого класу
Відомий вчений і практик в області геодезії С.Г. Судаков, узагальнюючи свій досвід побудови основних геодезичних мереж в СРСР [8], рекомендує для визначення очікування середньої квадратичної помилки положення пункту О по відношенню до суміжних пунктів формулу:
 ,
| (2.13) |
де mb — середня квадратична помилка вимірювання кутів;
а, в, с, s 1, s 2, s 3 — довжини сторін, зняті з карти, в метрах;
1, 2, 3 — кути, зняті з карти, в градусах.
Згідно з [4], для пункту планової мережі 3 класу, величина МO не повинна перевищувати 0,04 м.
Якщо виконується оцінка проекту вставки 4 кл., 1 або 2 розряду, то обчислюють очікувану відносну помилку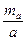 
визначення сторони, наприклад а (рис. 2.6)
 ,
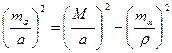| (2.14) |
де а — довжина сторони;
ma — середня квадратична помилка дирекційного кута сторони а, яку знайдемо з таких міркувань:
,
де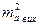 
— середня квадратична помилка вихідної сторони АВ;
mb — середня квадратична помилка вимірювання кута ОАВ.
Оскільки мова іде про взаємне положення сторони АО і АВ, то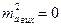 
.
Отже
ma2=mb2
або
ma=mb.
Формула (2.14) приймає вигляд
| (2.15) |
Згідно з Інструкцією [1], відносна помилка визначення сторони не повинна перевищувати
в 4 класі — 1:50000;
в 1 розряді — 1:20000;
в 2 розряді — 1:10000.
2.1.3.3 Оцінка запроектованого ряду
Якщо геодезична мережа запроектована у вигляді ряду трикутників, який опирається на дві вихідні сторони (такий варіант найбільш часто зустрічається в сучасних мережах згущення 1 і 2 розрядів), то оцінка проекту полягає в обчисленні відносної помилки найбільш слабкої сторони ряду (рис. 2.7)
 .
| (2.16) |
Найбільш слабкою стороною ряду є сторона, яка найбільше віддалена від вихідних сторін. Для прикладу на рис. 2.7 приведений ряд тріангуляції 1 розряду, вихідними для якого є сторони тріангуляції 4 класу АС і ВD. найбільш слабкою є сторона тріангуляції 1 розряду KL, віддалена від сторін АС і ВD на 4 трикутники. У формулі (2.16) 
— відносна середня квадратична помилка вихідних сторін,
mb — середня квадратична помилка вимірювання кутів;
Аі, Ві — зв’язуючі кути в трикутниках (кути, які приймають участь в передачі за теоремою синусів сторін від вихідної до найбільш віддаленої, наприклад, для рис. 2.7 — від AC до KL).
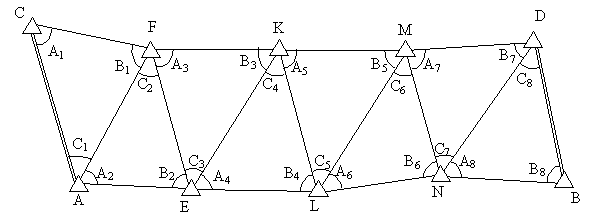
Рисунок 2.7 - Ряд тріангуляції
З рис. 2.7 запишемо
 .
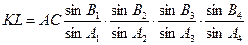| (2.17) |
Зв’язуючі кути вимірюють транспортиром з карти (в градусах).
У знаку суми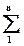 
, n — кількість трикутників, розміщених між найбільш віддаленою і вихідною сторонами.
Для рис. 2.7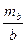 
слід прийняти 
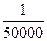, mb=5'', n=4.
Розрахунок виконують двічі: від двох вихідних сторін. Отримують величини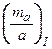 
і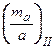 
.
За остаточне значення беруть середнє вагове з двох значень:
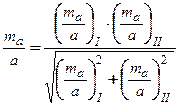
| (2.18) |
Якщо ця величина не перевищує граничного значення, то роблять висновок, що запроектований ряд трикутників відповідає необхідним технічним вимогам (для вище розглянутого прикладу відносна помилка визначення довжини в найбільш слабкому місці мережі тріангуляції 1 розряду не повинна перевищувати 1:20000).
2.2 Рекогностування пунктів тріангуляції
Рекогностування — це уточнення проекту на місцевості. В результаті рекогностування тріангуляційних пунктів уточнюють остаточні висоти зовнішніх знаків і місця, де будуть закладені пункти тріангуляції. Цю роботу виконує бригада, яку очолює досвідчений інженер-геодезист.
При уточненні висоти сигналу бригада керується тим же основним правилом, що і при проектуванні: між пунктами тріангуляційної мережі, по-перше, повинна бути забезпечена видимість, а, по-друге, висоти знаків повинні бути оптимальними. Вартість побудованих висот знаків на об’єкті буде найменшою, якщо сума їх висот буде мінімальною. Тому завдання бригади при рекогностуванні — розглянути безпосередньо на місцевості усі можливі варіанти, спрямовані на зменшення вартості будівельних робіт. Можливо, з цією метою навіть доведеться змінити місце розташування знаків, а іноді навіть повністю змінити проект.
У залежності від фізико-географічних умов місцевості рекогностування може бути різної складності. Для визначення висоти знаку в деяких випадках достатньо обмежитися простим оглядом місцевості. В інших випадках для цього необхідно виконати додаткові заміри рулеткою або стрічкою. Для цього необхідно піднятися на поруч розміщені споруди: будинки, стовпи, башти, дерева тощо, або в місці розміщення майбутнього знака підняти віхи чи встановити на оточуючих деревах яскраві маркувальні матеріали (марлю, папір, оберемок сіна або соломи тощо). Тому в спорядження бригади мають входити найлегші оптичні прилади (бінокль, технічний теодоліт), мірні засоби (рулетка або стрічка), підіймальні засоби (блоки, троси, канати, вірьовки тощо), засоби підняття на дерева, стовпи, будівлі (кігті, страхувальні пояси, каски та ін.).
Найкраще виконувати рекогностування безпосередньо з будівництвом знаків. Спочатку рекогностувальник встановлює висоти знаків вихідних пунктів, а висоти знаків наступних пунктів визначає, використовуючи побудовані знаки на попередніх пунктах.
Матеріали рекогностування використовуються будівельними бригадами при будівництві знаків.
2.3 Закладання центрів та будівництво зовнішніх знаків
Пункти тріангуляційних мереж закріплюються на місцевості центрами, над якими будуються зовнішні знаки. Центри служать для точного позначення місць розміщення пунктів і довготривалого їх збереження. Зовнішні знаки служать для встановлення на них приладів для спостережень, якщо відсутня видимість пунктів з землі, а також візирних цілей, на які проводяться спостереження з інших пунктів.
2.3.1 Закладання центрів
Типи центрів державних геодезичних мереж регламентуються “Інструкцією про типи центрів геодезичних пунктів” (ГКНТА — 2.01, 02–01–93), ГУГКіК, Київ, 1994 [3].
Для закріплення державних планових мереж застосовуються три види центрів: ґрунтові, скельні та центри на будівлі. Ґрунтові центризастосовуються на місцевості, де відсутнє залягання скелі до поверхні ґрунту ближче 1.8 м. Скельні центри застосовують при близькому заляганні скелі(до 1.8 м). При необхідності розміщення пунктів тріангуляції у містах центри встановлюють на будівлі (як правило, на даху).
Для закріплення пунктів астрономо-геодезичної мережі 1-го класу та геодезичної мережі 2-го класу Інструкція встановлює єдиний тип ґрунтового центру У10П.
Конструкція цього центру приведена на рис. 2.8.
Конструктивно центр складається з п’яти бетонних блоків з трьома металевими марками, що служать охоронними та пізнавальними елементами центра:
- нижній-бетонний куб з стороною 20 см з металевою маркою; об’єм — 0,008 м3, вага — 16 кг;
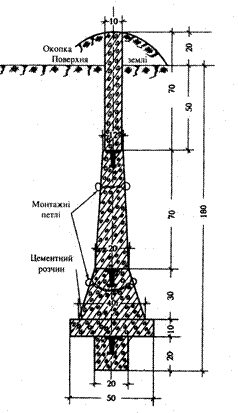
Рисунок 2.8 - Центр пункту тріангуляції, трилатерації, полігонометрії, 1 і 2 класів. Ґрунтовий. Тип У10П
- охоронна плита-бетонна плита 50´50´10 з арматурою із дроту Ø5 мм у вигляді сітки з стороною 10 см та двома монтажними петлями; об’єм — 0,025 м3, вага — 50 кг; верхній — бетонна зрізана піраміда з металевою маркою у верхній площині та монтажними петлями, нижня площина 20´20, верхня 14´14, висота 70 см; об’єм — 0,014 м3, вага — 28 кг;
- пізнавальний стовп — бетонний паралелепіпед 10´10´70; об’єм — 0,007 м3, вага — 14 кг.
Для закріплення пунктів геодезичної мережі 3-го класу Інструкція [3] встановлює тип ґрунтового центру У20П (рис. 2.9).
Центри пунктів тріангуляції, трилатерації, полігонометрії 3 та 4 класів споруджуються із чотирьох бетонних блоків з двома металевими марками:
- нижній — бетонний куб з стороною 20 см з металевою маркою, вага — 16 кг;
- охоронна плита — бетонна плита 50´50´10 з арматурою із дроту Ø5 мм у вигляді сітки з стороною 10 см та двома монтажними петлями, вага — 50 кг;
- верхній — бетонна зрізана піраміда з металевою маркою у верхній площині та монтажними петлями, нижня площина 20´20, верхня 14´14, висота 100 см, вага 40 кг;
- пізнавальний стовп — бетонний паралелепіпед 10´10´70, вага —
14 кг.
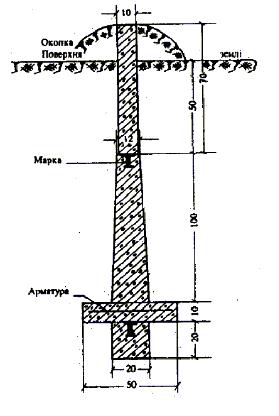
Рисунок 2.9 - Центр пункту тріангуляції, трилатерації, полігонометрії 3, 4 класів. Ґрунтовий. Тип У20П
У випадках близького залягання скелі збирається центр, який вміщує не менше двох блоків з металевими марками з обов’язковим бетонуванням нижнього центра у виїмку, вирубану у скелі, та встановленням на верхньому центрі пізнавального стовпа (тип У30П-при заляганні скелі до 1м, тип 140П – при заляганні скелі від 1 до 1,8 м). Центр типу У30П показаний на рис. 2.10, а типу 140П — на рис. 2.11.
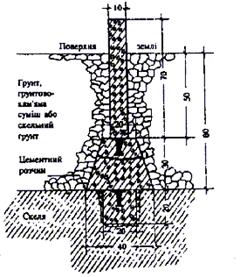
Рисунок. 2.10 - Центр пункту тріангуляції, трилатерації, 1, 2, 3, 4 класів. Скельний. Тип У30П застосовується при заляганні скелі від поверхні землі до 1 м)
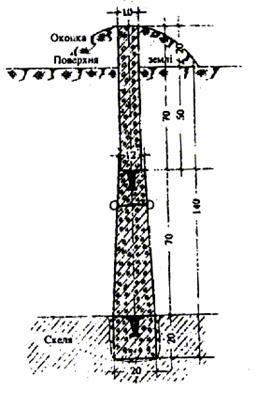
Рисунок 2.11 - Центр пункту тріангуляції, трилатерації, полігонометрії 1, 2, 3, 4 класів.Скельний. Тип 140П
(застосовується при заляганні скелі від поверхні землі від 1м до 1,8м)
Якщо пункт тріангуляції необхідно закріпити на будівлі, застосовують центр типу У16 (рис. 2.12).
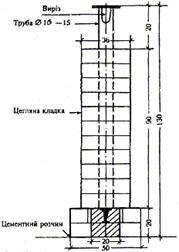
Рисунок 2.12 - Центр пункту тріангуляції, трилатерації, полігонометрії 1, 2, 3, 4 класів на будівлі. Тип У16.
Крім центрів, на кожному пункті планової геодезичної мережі 2 класу необхідно встановити два орієнтирні пункти (ОРП). Їх призначення — служити для азимутальних прив’язок геодезичних мереж нижчого класу в разі, якщо на зовнішній знак, звідки є видимість на суміжні пункти мережі, піднятися немає можливості (підгнили ноги знаку, зруйнована драбина, знак повністю зруйнований тощо); служити для швидкого орієнтування на пункті (наприклад, в разі військових дій), в випадку складних метеорологічних умов (туман, імла, дощ). На центри орієнтирних пунктів має бути видимість як зі столика сигналу, так і з землі.
Закладають ОРП на віддалі 500–1000 м (на забудованій території — не менше 250 м) від пункту тріангуляції. Для полегшення пошуку ОРП закладають так, щоб кут між напрямками на них складав приблизно 90 градусів. Орієнтирному пункту, у якого азимут менший, присвоюють №1, другому — №2.
Для закріплення ОРП на місцевості застосовується центр типу У5
(рис. 2.13).
Рисунок 2.13 - Орієнтирний пункт. Тип У5.
На пунктах планової мережі 3 класу ОРП закладаються лише в тому випадку, якщо не забезпечується безпосередньо з землі видимість (земля — земля) між суміжними пунктами мережі.
Пункти планових мереж 1 і 2 розрядів закріплюються менш капітальними центрами, висота яких становить 70–75 см. На незабудованих територіях закладають центр типу У15Н. На рис. 2.14. показана конструкція цього центру, розміри, а також форма зовнішнього оформлення у вигляді круглої канави з внутрішнім діаметром 130 см, зовнішнім — 180 см і глибиною 30 см.
Рисунок 2.14 - Центр пункту планової мережі 1 і 2 розрядів
для незабудованої території. Тип У15Н
На забудованих територіях закладають центри типу У15, У15К
(рис. 2.15).
| 
|
| а) | б) |
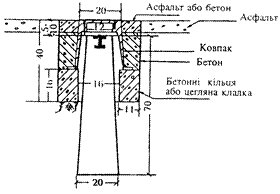
Рисунок 2.15 - Центр пункту полігонометрії 1 і 2 розрядів:
а) для територій райцентрів, міст, селищ, сільських населених пунктів (тип У15);
б) для міста Києва, Севастополя та обласних центрів (тип У15к).
Виготовлення центрів здійснюється, як правило, централізованим шляхом за замовленнями геодезичних організацій на заводах залізобетонних конструкцій. При цьому використовуються багатосекційні опалубки, вібратори для ущільнення бетону, бетонозмішувачі та інша техніка.
Закладання центрів здійснюється з допомогою техніки (автоямобурів, екскаваторів) або вручну, із застосуванням найпростіших інструментів.
2.3.2 Будівництво зовнішніх знаків
На пунктах планової геодезичної мережі будують зовнішні знаки таких основних типів:
- піраміда;
- простий сигнал;
- складний сигнал.
Будуються знаки дерев’яні або металічні.
Піраміда будується в тому випадку, коли спостереження на пункті можна виконати зі штатива (рис. 2.16). На пунктах державних мереж 2 і 3 класу будують чотиригранні піраміди, на пунктах мереж згущення 4 класу, 1 і 2 розряду можуть будуватися тригранні піраміди. Висота піраміди 5 –
8 м.
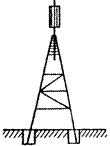
Рисунок 2.16 - Піраміда
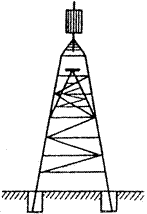
Простий сигнал — це геодезичний знак, який складається з двох пірамід: внутрішньої і зовнішньої. Внутрішня, трикутна піраміда, несе на собі столик для встановлення на ньому приладу (теодоліта, світловіддалеміра тощо). Зовнішня, чотирикутна зрізана піраміда, служить для встановлення на ній площадки для спостерігача та даху з візирною ціллю (рис. 2.17). Піраміди не дотикаються одна до другої.
| 
|
| Рисунок 2.17 - Простий сигнал | Рисунок 2.18 - Складний сигнал |
Прості сигнали будують у випадках, коли геодезичний прилад треба підняти на висоту від 4 до 10 м.
Складні сигнали будують у тих випадках, коли геодезичний прилад треба підняти на висоту від 11 до 40 м. Складний сигнал складається також з двох пірамід: зо
