Вектором намагничивания называется векторная физическая величина, равная векторной сумме магнитных моментов молекулярных токов в единице объёма вещества (магнетика)

Единицей измерения намагниченности в системе СИ является ампер, делённый на метр

(А/м).

Определим, чему равен поток вектора магнитной индукции через любую замкнутую поверхность с учётом полей молекулярных токов:

Силовые линии магнитного поля всегда замкнуты, очевидно, что линии полей, созданных молекулярными токами, тоже будут замкнутыми. В результате, каждая силовая линия пересекает замкнутую поверхность как минимум дважды. Причём один раз она входит в поверхность и считается положительной, второй раз –выходит из неё и считается отрицательной. Поэтому оба интеграла будут равны нулю, т.е.

Поток вектора магнитной индукции через любую замкнутую поверхность всегда равен нулю.

Запишем теорему о циркуляции вектора с учетом молекулярных токов:

- как циркуляция вектора магнитной индукции внешнего поля, образованного макротоками.

тоже должен определяться суммой всех молекулярных токов, т.е.

Окончательно получим:

Можно доказать, что , где проекция вектора намагничивания на направление .

Подставив этот интеграл в выражение отмеченное звёздочкой получим:

Напряжённостью магнитного поля называют векторную величину равную:

Векторы и не являются аналогами друг друга. Существенным отличием является то, что циркуляцию по замкнутому контуру определяют только реальные токи, охватываемые рассматриваемым контуром без учёта среды.

В вакууме =0, и тогда .

Реакцию среды на внешнее магнитное поле характеризуют коэффициентом намагничивания или магнитной восприимчивостью (хи).

Для изотропного магнетика получим:

и называется магнитной проницаемостью.

Виды магнетиков

В зависимости от знака и величины магнитной восприимчивости все вещества можно разделить на три группы:

1. Диамагнетики - это вещества, у которых и очень мала по величине . Магнитная проницаемость этих веществ практически равна единице .

2. Парамагнетики - у этих веществ и составляет величину порядка . Проницаемость парамагнетиков больше единицы .

3. Ферромагнетики - это вещества, у которых и ее значения близки к единице. Магнитная проницаемость ферромагнетиков может достигать очень больших значений

(несколько десятков тысяч). Отличительной особенностью ферромагнетиков является сложная зависимость от индукции внешнего магнитного поля В, а также зависимость намагниченности от предыстории образца. Это свойство называется гистерезисом и заключается в том, что после намагничивания внутреннее поле сохраняется даже при выключении внешнего поля.

Природа молекулярных токов, существование которых было предсказано Ампером, стала понятной после опытов Резерфорда и построения им планетарной модели атома.

По Резерфорду атом представляет собой электродинамическую систему, в центре которой находится крохотное положительно заряженное ядро, вокруг которого вращаются по круговым орбитам отрицательные электроны.

Пусть электрон двигается вокруг ядра и за единицу времени он делает 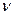оборотов. При этом через элементарную площадку , расположенную перпендикулярно на пути электрона, переносится заряд, равный

Т.Е движущейся электрон можно рассматривать как эквивалентный ток, Поскольку этот ток является круговым, то его можно рассматривать как контур с током, сила которого равна

Магнитный момент такого контура равен , где радиус орбиты электрона.

Линейная скорость электронов на орбите равна , тогда магнитный момент можно записать:

Магнитный момент, обусловленный движением электрона по круговой орбите вокруг атомного ядра, называется орбитальным магнитным моментом электрона.

Направление орбитального магнитного момента связано с направлением эквивалентного тока правилом правого винта.

Эквивалентный ток течёт в противоположную

сторону направлению движения электрона, т.к. за

положительное направление тока выбирается

движение положительно заряженных частиц.

Рис 35

Любое материальное тело, вращающееся по окружности обладает механическим моментом (моментом импульса).

где импульс электрона, равный , и поскольку , то , тогда

Или

Отношение орбитального магнитного момента элементарной частицы к её механическому моменту называют гиромагнитным отношением.

Экспериментальное наблюдения гиромагнитных эффектов (т.е. вращение тела при намагничивании и намагничивание при вращении) позволили рассчитать гиромагнитное отношение для электрона. Оказалось, что его экспериментальное значение в два раза больше расчетного. Это позволило предположить, что за магнитные свойства вещества ответственен не орбитальный магнитный момент.

Позднее было установлено, что кроме орбитального момента электрон обладает собственными магнитным и механическими моментами, для которых гиромагнитное отношение было равно:

Что совпадало с экспериментальными результатами де Хааса и Барнета.

ЛЕКЦИЯ 8

ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ

1. ЭДС индукции. Закон электромагнитной индукции.

2. ЭДС индукции в движущемся проводнике.

3. Явление самоиндукции.

4. Токи замыкания и размыкания.

5. Энергия магнитного поля.

В 1831 году Майкл Фарадей обнаружил, что в замкнутом проводящем контуре при изменении магнитного потока через поверхность, ограничивающую данный контур, возникает электрический ток.

Это явление было названо электромагнитной индукцией, а возникающий ток – индукционным.

Возникновение электрического тока в контуре свидетельствовало о возникновении электродвижущей силы – эдс индукции .

Фарадей показал, что величина эдс индукции не зависит от способа изменения магнитного потока и определяется только скоростью изменения магнитного потока.

Знак минус в законе Фарадея определяет полярность эдс индукции и, следовательно, направление индукционного тока.

На основании экспериментальных данных было сформулировано правило Ленца, которое устанавливает, что

эдс индукции возбуждает в контуре ток, индукция магнитного поля которого всегда противодействует первоначальному изменению магнитного потока.

Будем считать, что магнитный поток через контур возрастает. Направление

индукционного тока должно быть таково, чтобы его

магнитное поле препятствовало росту внешнего поля,

т.е. ток в контуре течёт по часовой стрелке. При

уменьшении индукции внешнего поля уменьшается и

магнитный поток, теперь магнитное поле

индукционного тока будет поддерживать убывающее

внешнее поле и ток в контуре течёт против часовой

стрелки.

Рис.36

Возьмём контур с подвижной перемычкой и поместим его в магнитное поле,

направленное перпендикулярно плоскости

контура. При движении перемычки со

скоростью V на каждый электрон будет

действовать сила Лоренца, направленная вдоль

перемычки и равная:

Рис.37

Под действием этой силы электроны начнут перемещаться вдоль перемычки со скоростью . То есть, действие силы эквивалентно действию на электрон электрического поля, напряженность которого равна:

Это поле имеет не электростатическую природу и его циркуляция по замкнутому контуру даёт величину эдс, возникающую в этом контуре.

Умножим и разделим правую часть, полученного соотношения на . В результате получим:

где ;

Знак минус появляется, так как и имеют разные знаки.

В рассмотренном нами случае роль сторонней силы, поддерживающей ток в контуре, играет сила Лоренца, перемещающая электрон в магнитном поле. Ранее мы получили, что работа силы Лоренца должна всегда быть равна нулю, чему противоречит полученный сейчас результат .

Однако пока мы не учитывали, что при движении электрона вдоль перемычки со скоростью , на него действует сила, модуль которой равен:

Полная же сила Лоренца равна: . Работа этой силы за время равна

(*)

Причём направления и U- одинаковы, а

и V противоположны.

Подставив в выражение (*) выражения,

определяющие и , получим:

Рис.38

Таким образом, работа полной силы Лоренца действительно будет равна нулю.

Поскольку сила направлена против скорости V, то для того чтобы эта скорость оставалась постоянной, к перемычке необходимо приложить внешнюю силу, уравновешивающую силу , приложенную к электронам. Энергия, возникающая при совершении этой силой работы, выделяется в виде тепла при прохождении индукционного тока.

Итак, изменение магнитного потока ведет к возникновению электрического поля, эффективная напряженность которого равна и циркуляция которой по замкнутому контуру не равна нулю. Это существенно отличает возникающее поле от поля, созданного неподвижным зарядом. Следовательно, силы, действующие в этом поле являются неконсервативными, а само поле непотенциальное.

Пусть в некотором контуре течёт ток, сила которого равна I. Этот ток будет создавать магнитное поле, пронизывающее данный контур, и, индукция которого, согласно закону Био-Савара-Лапласа пропорциональна силе тока I. При изменении силы тока в контуре будет меняться индукция магнитного поля , а, следовательно, и магнитный поток . Это, в свою очередь, должно привести к возникновению индукционного тока, который будет препятствовать изменению основного тока I.

Самоиндукцией называется физическое явление, заключающееся в возникновении эдс индукции при изменении силы основного тока в контуре.

Так как индукция магнитного поля В пропорциональна силе тока I, то и магнитный поток тоже пропорционален силе тока.

- коэффициент пропорциональности между силой тока в контуре и магнитным потоком, пронизывающим данный контур, называется индуктивностью данного контура.

За единицу индуктивности в системе СИ принимается индуктивность такого проводника, у которого при силе тока в 1 ампер возникает магнитный поток, равный 1 вебер. Эта единица называется Генри.

Индуктивность зависит от геометрической формы контура, его размеров и магнитных свойств окружающей среды.

Индукционный ток, возникающий при самоиндукции, согласно правилу Ленца направлен так, чтобы его магнитное поле препятствовало изменению магнитного поля основного тока в контуре. Это приводит к тому, что установление тока при замыкании или размыкании цепи происходит не сразу, а постепенно.

Похоже, что индуктивность играет ту же роль, что и масса при изменении скорости.

Индуктивность – физическая величина, характеризующая инерционные свойства контура по отношению к изменению силы тока в нём.

В случае самоиндукции возникающая в контуре эдс равна:

Если контур жесткий (т.е. не меняет своей формы) и окружающая среда- вакуум, то последнее слагаемое будет равно нулю. Так как L = const.

При наличии магнитной среды зависимость , где - магнитная проницаемость среды, будет довольно сложная, так как значения проницаемости будут меняться в зависимости от величины индукции внешнего магнитного поля.

А) Токи замыкания

Рассмотрим электрическую цепь, состоящую из индуктивности L, источника тока и ключа К, который имеет два положения А и Б и который позволяет включать и отключать без разрыва основной цепи.

Пусть R – общее сопротивление цепи, включая и

внутреннее сопротивление источника.

При включении ключа в положение А источник

подключён к катушке индуктивности L.

Ток в катушке индуктивности установится не сразу.

При нарастании силы тока в катушке возникнет эдс

самоиндукции , которая создаст ток,

препятствующий, установлению максимального тока.

Рис.39

По второму правилу Кирхгофа сумма падений напряжений в замкнутом контуре равна алгебраической сумме действующих в цепи эдс, т.е.

(1)

Общий ток в цепи состоит из основного тока и тока самоиндукции

(2)

Продифференцировав это выражение по t, получим

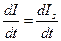
(3)

Подставив (2) и (3) в (1), получим

Разделим переменные .

Пределы интегрирования определим из следующих соображений:

Время меняется от 0 до ; при этом ток самоиндукции меняется от до . Это следует из того, что при ток I в цепи равен нулю, тогда согласно (2) .

После потенцирования получим .

Подставим в (2) полученное

Б) Токи размыкания.

Отключим источник тока , для этого перебросим ключ в положение Б.

Ток в цепи начнет убывать и эдс самоиндукции поменяет знак и будет поддерживать убывающий ток. Обозначим общее сопротивление цепи r (нет внутреннего сопротивления источника).

В цепи действует только эдс самоиндукции и по второму правилу Кирхгофа получим:

. (1)

За время от - время отключения источника до t – ток изменится от до I.

Проинтегрировав выражение (1), получим:

После потенцирования получим закон изменения силы тока в разомкнутой цепи:

График зависимости тока разрядки от времени имеет вид представленный на рис. 19.

Рис.40.

Если просто разомкнуть цепь, содержащую индуктивность, то r (разрыв цепи). Тогда эдс самоиндукции будет тоже стремиться к бесконечности и индукционный ток может превышать основной ток в несколько раз.

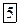
Что бы в катушке индуктивности L проходил электрический ток, меняющейся со скоростью , должна совершаться работа равная:

где N – мощность электрического тока. ;

Полная работа тока будет равна:

Эта работа идёт на увеличение энергии запасённой катушкой индуктивности, по которой течёт ток, следовательно, можно утверждать, что энергия, сосредоточенная в катушке индуктивности равна:

Выразим энергию катушки через параметры, характеризующие магнитное поле.

Пусть магнитное поле сосредоточено в бесконечно длинном соленоиде, индуктивность которого равна:

где - магнитная проницаемость среды, - магнитная постоянная, n- число витков на единицу длины соленоида, V – объём соленоида.

Тогда энергию катушки можно записать:

Умножив и разделив правую часть на , получим:

Учитывая, что индукция магнитного поля в бесконечном соленоиде равна: , запишем выражение, определяющее объёмную плотность энергии магнитного поля:

Так как , где H – напряжённость магнитного поля, можно объёмную плотность энергии магнитного поля выразить через напряжённость этого поля:

ЛЕКЦИЯ 9

ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ.

1. Собственные электромагнитные колебания

2. Затухающие электромагнитные колебания.

3. Вынужденные электромагнитные колебания.

4. Переменный ток. Закон Ома дл переменного тока.

Любая электрическая цепь помимо источника питания (эдс) может содержать три основных элемента: резистор (сопротивление), конденсатор (емкость) и катушку индуктивности.

Пусть схема состоит из двух элементов: катушки индуктивности L и конденсатора C, соединенных в замкнутый контур. Наличием активного сопротивления соединительных проводов будем пренебрегать. Такой контур называют идеальным.

Пусть в начальный момент конденсатор C заряжен так,

что на одной из его пластин имеется заряд , а на

другой . В момент t=0 конденсатор начинает

разряжаться через катушку индуктивности. В каждый

момент времени разность потенциалов на обкладках

конденсатора будет равна:

где q- заряд конденсатора в данный момент времени.

Рис.41

По мере разрядки конденсатора ток в катушке индуктивности нарастает. При этом в катушке индуктивности будет возникать эдс самоиндукции равная:

В момент полной разрядки конденсатора сила тока в катушке достигнет максимума.

Т.Е, если в начальный момент вся энергия контура была сосредоточена в конденсаторе в виде энергии электрического поля, то по мере разрядки конденсатора и увеличении силы тока в катушке, эта энергия будет переходить в энергию магнитного поля.

В момент , когда сила тока станет максимальной, эдс самоиндукции поменяет знак и будет поддерживать убывающий ток. Это приведет к тому, что на обкладках конденсатора появятся заряды противоположного знака, т.е. конденсатор будет перезаряжаться.

И если потерь энергии в конденсаторе нет, то в момент на пластинах окажется заряд , но противоположного знака.

В дальнейшем процесс повторится.

Основываясь на 2-ом правиле Кирхгофа, можно записать:

Учитывая, что , получим

или

Это однородное дифференциальное уравнение второго порядка описывает свободные гармонические колебания в идеальном колебательном контуре, решение этого уравнения имеет вид

- частота собственных колебаний в контуре, равная ;

начальная фаза колебаний.

Период собственных колебаний заряда в идеальном колебательном контуре соответственно будет равен .

Поскольку напряжение в контуре равно , следовательно оно изменяется со временем по закону:

- амплитуда напряжения.

Закон изменения силы тока в таком контуре будет иметь вид:

Амплитуда силы тока равна: .

Учитывая формулы приведения, получим:

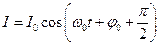Получили, что заряд и напряжение в колебательном контуре изменяются синфазно, а ток опережает их колебания на .

Процесс электромагнитных колебаний обусловлен перекачкой энергии из конденсатора (в виде энергии электрического поля) в энергию катушки (в виде энергии магнитного поля)

Учитывая, что , получим

Рис.42

Полная энергия колебательного контура складывается из энергии электрического и магнитного полей, следовательно

Т.Е, полная энергия идеального колебательного контура является постоянной величиной.

В идеальном колебательном контуре мы не учитывали наличие активного сопротивления, которое обязательно есть в любой реальной цепи.

Пусть контур содержит три элемента: конденсатор С, катушку индуктивности L и резистор, сопротивление которого R, соединенные последовательно.

Сообщим конденсатору заряд . При разрядке

конденсатора через резистор и катушку часть

энергии электрического поля перейдет в джоулево

тепло.

Рис.43

Согласно 2-ому правилу Кирхгоффа, можно записать:

Или, учитывая что : , получим

Это однородное дифференциальное уравнение 2-го порядка описывает затухающие колебания в реальном колебательном контуре.

Решение этого дифференциального уравнения, представляющее закон изменения заряда, можно представить в виде:

, где - частота затухающих колебаний.

Разделив функцию, описывающую изменение заряда на С, получим закон изменения напряжения на конденсаторе:

= .

Что бы найти закон изменения силы тока продифференцируем функцию по времени:

Умножим правую часть полученного выражения на

В результате получим:

Введем угол , исходя из условий, что:

;

Подставив эти тригонометрические функции в закон изменения силы тока, получим:

Таким образом, при , ток опережает по фазе напряжение U на величину большую чем .

Скорость уменьшения амплитуды колебаний в реальном колебательном контуре характеризует логарифмический декремент затухания, который равен:

где - амплитуда колебаний в данный момент времени,

амплитуда колебаний через период.

- логарифмический декремент затухания обратно пропорционален числу колебаний, совершаемых за время, в течение которого амплитуда уменьшается в е раз.

Вынужденными называются колебания, совершаемые под действием внешней периодически изменяющейся силы.

Если подключить к колебательному контуру переменную эдс , то в контуре возникают вынужденные колебания. В этом случае в контуре действует две эдс.

На основании 2-го правила Кирхгоффа можно записать:

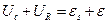
где и - амплитуда и частота внешней эдс, соответственно.

Это неоднородное дифференциальное уравнение второго порядка, решение которого можно представить в виде суммы частного решения неоднородного уравнения, имеющего вид:

и общего решения однородного уравнения вида:

Последняя функция описывает колебания при переходном процессе малой длительности, и можно считать, что установившиеся колебания, описываются решением вида:

где максимальное значение заряда на конденсаторе, разность фаз между колебаниями заряда и внешней эдс.

и не зависят от начальных условий и определяются только свойствами контура и величиной внешней эдс.

Подставив в дифференциальное уравнение вынужденных колебаний, получим, что эта функция является решением этого уравнения, если: и .

Полученные выражения показывают, что амплитуда заряда зависит от разности частот собственных колебаний и внешней эдс . Максимум достигается, если скобка под корнем равна нулю, т.е. .

Рис 43.

Закон изменения силы тока найдем, продифференцировав по времени:

Явление резонанса – это возбуждение в контуре колебаний большой амплитуды при частоте внешней эдс равной или близкой к частоте собственных колебаний данного контура

Существенное значение при резонансе имеет величина активного сопротивления контура R.

Если исследовать на экстремум функцию, определяющую зависимость амплитуды от частоты , то получим:

Т.е. резонансная частота всегда меньше частоты собственных колебаний контура.

Одной из характеристик, определяющих отклик колебательной системы на внешнее периодическое воздействие, является добротность .

где - разность частот в точках на высоте 0,7 .

Из графика видно, что чем больше

добротность, тем острее резонансная

кривая.

Рис. 44

Переменным будем называть ток, сила которого изменяется по синусоидальному закону.

где амплитудное или пиковое значение силы тока, - его частота.

Более удобно характеризовать переменный ток эффективными значениями силы тока и напряжения.

;

Эффективным значением силы переменного тока называется сила такого постоянного тока, при прохождении которого по той же цепи выделяется такая же мощность, что и при прохождении переменного тока.

1. Резистор в цепи переменного тока

Подключим резистор с сопротивлением R к переменной эдс . Сила тока через резистор

будет изменяться согласно закону Ома:

отсюда следует, что:

Рис.45 где .

Как видно, сила тока и напряжение в данном случае изменяются синфазно.

Рис.46.

Электрическая энергия в резисторе переходит только в тепло и средняя мощность, выделяющаяся в цепи равна:

2. Конденсатор в цепи переменного тока.

Рис.47. Рис. 48.

При подключении конденсатора с емкостью C к переменной эдс через него будет течь переменный ток. Это происходит потому, что при подключении переменного напряжения

Происходит перетекание заряда с одной обкладки на другую, но не успевает конденсатор полностью разрядится, как эдс меняет полярность, и заряды начинают течь в обратном направлении.

Согласно второму правилу Кирхгоффа эдс источника в любой момент должно быть равна напряжению в цепи на обкладках конденсатора

; ; .

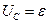Т.е заряд на конденсаторе меняется в одной фазе с напряжением.

Закон изменения силы тока в цепи найдем, продифференцировав по времени:

Воспользовавшись формулами приведения, перепишем закон изменения силы тока в виде

, где

Т.е. в конденсаторе сила тока и напряжение не совпадают по фазе. Ток опережает напряжение на .

Согласно закону Ома в резисторе: .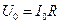

По аналогии запишем, что , .

называется реактивным емкостным сопротивлением цепи переменного тока и измеряется в Омах.

3. Индуктивность в цепи переменного тока.

Подключим катушку с индуктивностью L к переменной эдс . Будем считать, что активное сопротивление самой катушки и подводящих проводов пренебрежимо мало.

В данном случае в цепи действует две эдс: эдс

самоиндукции и переменная эдс , равная

Согласно 2-ому правилу Кирхгоффа можно

записать:

Рис. 49

Найдем силу тока в цепи. Для этого разделим переменные, а затем проинтегрируем правую и левую части полученного уравнения:

Поскольку , перепишем полученное выражение:

где .

Получается, что сила тока в катушке отстает от внешней эдс на .

Рис.50

Соотношение между амплитудными значениями силы тока эдс, учитывая закон Ома, можно записать:

И так как , получим, что . Это реактивная составляющая полного сопротивления называется индуктивным сопротивлением.

4. R,L,C цепочка в цепи переменного тока.

Если цепь состоит из последовательно соединенных резистора, конденсатора и катушки индуктивности, то полное сопротивление такой цепи будет равно:

Z- называется электрическим импедансом цепи.

В этом случае закон Ома будет иметь вид:

. Рис.51.

При этом ток будет отставать от напряжения на угол , у которого .

Изобразим это с помощью векторной диаграммы..

Пусть ось токов совпадает с осью OX.

напряжение на резисторе совпадает по

током, следовательно, вектор, модуль

которого равен амплитудному значению

напряжения будет направлен по

оси OX.

Напряжение на катушке опережает ток на

, и, следовательно, вектор, модуль

которого равен , направлен по

Рис. 52 оси OY.

Напряжение на конденсаторе отстает по фазе от тока на , поэтому, соответствующий вектор, модуль которого равен , направлен вниз по оси OY.

Направление вектора, определяющего модуль результирующего напряжения U, получим путем векторного сложения всех трех векторов, и его численное значение будет равно:

Разность фаз между колебаниями тока и напряжения в R,L,C цепочке равна углу, у которого:

Амплитуда силы тока достигает своего максимального значения при наименьшем значении полного сопротивления Z, т.е.

Сдвиг по фазе между колебаниями внешней эдс и силой тока при этом становится тое равным нулю. Активная мощность совпадает с мощностью источника.

Амплитуды напряжения на катушке и конденсаторе в этом случае одинаковы по величине, но противоположны по фазе. Полное падение напряжения в цепочке равно падению напряжения на активном сопротивлении. Это явление называется резонансом напряжений.

Если контур состоит из параллельно соединенных конденсатора и катушки индуктивности

при малых значениях активного сопротивления

параллельных ветвей амплитуда

силы тока во внешне части цепи равна:

При и тогда

Рис.53

Резкое уменьшение амплитуды силы тока во внешней цепи, питающей параллельно соединенные емкостное и индуктивное сопротивления при условии, что называется резонансом токов.

ЛЕКЦИЯ 10

ВЗАИМНЫЕ ПРЕВРАЩЕНИЯ ЭЛЕКТРИЧЕСКИХ И МАГНИТНЫХ ПОЛЕЙ.

УРАВНЕНИЯ МАКСВЕЛЛА.

1. Ток смещения.

2. Вихревое электрическое поле.

3. Уравнения Максвелла в интегральной форме.

4. Электромагнитное поле. Уравнения классической физики.

Пусть конденсатор емкостью C включен в сеть переменного тока. В диэлектрике между пластинами А и В заряды не могут перемещаться, в результате линии тока, подходящего к пластинам обрываются, т.е. ток проводимости оказывается разомкнутым.

Пусть в начальный момент обкладка А имеет

Положительный заряд, распределенный по ее

Поверхности с плотностью . Обкладка В

Имеет отрицательный заряд с поверхностной

Плотностью . При разрядке конденсатора

Ток течет от А к В по внешней цепи и

Плотность этого тока будет равна:

. ()

Рис.54.

Будем считать, что частота переменного тока не велика, что даст нам возможность оперировать мгновенными значениями для вычисления мгновенных значений параметров поля между пластинами.

Численное значение вектора электростатической индукции в пространстве между пластинами, как известно из электростатики, равно: .

Продифференцировав по времени, получим:

или . ()

В случае неоднородного поля надо перейти к частным производным, что мы в дальнейшем и сделаем.

В конденсаторе направление вектора от пластины А к В, а вектора от В к А, так как поле в конденсаторе при его разрядке убывает. Следовательно Учитывая и получим: