ЦЕЛЬ РАБОТЫ
Изучение процессов заряда и разряда конденсаторов в RC -цепях, ознакомление с работой приборов, используемых в импульсной электронной технике.
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ РАБОТЫ
Рассмотрим схему, пред-ставленную на рис. 1. Схема включает в себя источник постоянного тока, активное сопротивление и конденсатор, процессы заряда и разряда в котором и будем рассматривать. Эти процессы разберем по-отдельности.
Рис. 1
Разряд конденсатора.
Пусть вначале источник тока e подключен к конденсатору С через сопротивление R. Тогда конденсатор зарядится так, как показано на рис. 1. Переведем ключ К из положения 1 в положение 2. В результате конденсатор, заряженный до напряжения e, начнет разряжаться через сопротивление R. Считая ток положительным, когда он направлен от положительно заряженной обкладки конденсатора к отрицательно заряженной, можем записать
, 
, 
, (1)
где i – мгновенное значение силы тока в цепи, знак «минус» которого показывает, что появление тока в цепи i связано с уменьшением заряда q на конденсаторе;
q и С – мгновенные значения заряда и напряжения на конденсаторе.
Очевидно, что первые два выражения представляют собой определения силы тока и электроемкости, соответственно, а последнее – закон Ома для участка цепи.
Из двух последних соотношений выразим силу тока i следующим образом:
.
Тогда можно записать уравнение
. (2)
Это дифференциальное уравнение, решением которого является экспоненциальная функция вида
, (3)
где q0 – заряд конденсатора в начальный момент времени t =0;
– время релаксации RC -цепи, измеряемое в секундах.
Если с начала разряда конденсатора пройдет время t=t, то, согласно (3), заряд уменьшится в е раз (е =2,71 – основание натурального логарифма). Поэтому по порядку величины t равна времени полного разряда конденсатора.
Поделив обе части уравнения (3) на величину емкости С, получим
e 
, (4)
где e =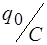 
– напряжение на конденсаторе в начальный момент времени t =0.
Зависимость напряжения на конденсаторе от времени в рассмотренном процессе показана на рис. 2.
Зная данную зависимость, можно вычислить время q, за которое напряжение на конденсаторе уменьшится в 2 раза. Подставив значение 
U = e /2 в уравнение (4), получим
Рис. 2
e 
= e 
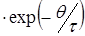, (5)
откуда можно получить значение
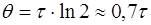. (6)
