Математические формулы

 

Язык формул — особый и, добавим, международный язык. У него свои, твердо установленные правила. Каждый элемент формулы — буква, цифра, знак— обозначает определенное понятие. К тому же каждый из этих элементов может получить иное значение, если изменить характер его начертания, размер и расположение. Поэтому для того, чтобы смысл формул не искажался и был ясен читателям, в их наборном оформлении необходима логичная, общепризнанная и последовательно проводимая система. Эта система определяет в основном характер (начертание) применяемых шрифтов и специальных знаков, их кегль, а также взаимное расположение частей и элементов формулы.

 

Формулу, набранную бессистемно, труднее прочитать и понять, однако только опытный глаз может сразу определить, в чем ее наборное оформление неправильно или непоследовательно, что в нем надо упорядочить. Поэтому в приводимых далее примерах показаны некоторые сложные случаи наборного оформления формул. Внимательное рассмотрение их поможет читателю яснее понять основные положения системы, о которой мы упоминали.

 

Цифры в формулах служат для обозначения чисел, как и в любом другом тексте; поэтому для них применяется шрифт обычного, т. е. прямого светлого начертания.

 

Для условных обозначений величин (символов) используют буквы латинского, а также греческого и (реже) готического алфавитов.

 

Буквы латинского алфавита, обозначающие величины, применяются в курсивном начертании; так они резче отличаются и не могут быть спутаны при чтении с элементами обычного текста (например, обозначение величины а отличается от союза «а», величины с — от предлога «с»). В некоторых разделах математики необходимы буквы латинского алфавита двух начертаний. В качестве второго принято прямое полужирное, причем обычно не своей гарнитуры, а какой-либо гротесковой (для более сильного выделения).

 

Буквы греческого и готического алфавитов могут применяться как прямого, так и курсивного начертания (в обоих начертаниях они достаточно отличаются от русских и латинских), но единообразно во всем издании.

 

Для условных сокращений математических терминов (например, sin, arctg, lim, max) тоже применяется шрифт латинского алфавита, но в прямом начертании (в отличие от обозначений величин). По аналогии прямой шрифт используют и в тех случаях, когда условные сокращения даны буквами русского алфавита (например, cн в смысле c нормальное, в отличие от сn, то есть с энное).

 

Сокращенные наименования метрических мер и технических единиц измерения, обозначенные буквами латинского алфавита, тоже даются прямым шрифтом (50 kg, 120 v). Если же они обозначаются буквами русского алфавита, то обычно,— но не обязательно, применяется курсив (50 кг, 120 в).

 

Что касается кегля, то для однострочных формул (за исключением индексов, показателей степени и некоторых специальных знаков) обычно используют шрифт того же кегля, что и для основного текста книги.

 

Двухстрочные же (или многострочные) части формулы, то есть дроби, набираются двояко — шрифтом такого же кегля, что и однострочные формулы, или же шрифтом несколько пониженного кегля, например петитом, если однострочные части формул набираются корпусом (пример 20).

 

Каждый из этих способов имеет свои достоинства и недостатки. В первом случае одна и та же величина в любой формуле данного издания изображается буквой или цифрой одинакового кегля, что вполне логично. Однако при этом формула менее компактна. Во втором — строгая логичность в какой-то мере нарушается, но зато формула становится компактнее, и хорошо подготовленный читатель легче охватит ее глазом. Кроме того, этот способ экономичнее первого.

 

В практике советских издательств первый способ применяется в книгах для малоподготовленного читателя, в частности в учебниках для средней школы, где к тому же формулы несложны и легко охватываются глазом, если даже двухстрочия набраны корпусом. В книгах для подготовленного читателя (в научной литературе) до недавнего времени пользовались вторым способом. Однако в последние годы произошли изменения в технике набора — стало возможным набирать двухстрочные и даже четырехстрочные формулы на наборных и фотонаборных машинах, но обычно при одинаковом кегле для однострочных и двухстрочных (многострочных) частей формулы.

 

Показатели степени и индексы должны быть значительно меньше букв и цифр в основной строке, чтобы четко отличаться от них, и примерно наполовину выступать над (или под) выражением, к которому они относятся.

 

Математические знаки четырех действий, знаки геометрических образов, а также знаки, показывающие соотношение левой и правой частей формулы, набираются таким же кеглем, как и вся строка, к которой они относятся.

 

Однако для некоторых знаков необходим больший размер:

скобки должны охватывать (по высоте) все заключенное в них выражение;

знак радикала v должен соответствовать по высоте подкоренному выражению вместе с приставной линейкой, прикрывающей это выражение сверху;

знаки суммы?, произведения? и интеграла? относятся к целому выражению; сигналом этого является их более крупный кегль по сравнению с другими элементами формулы: в однострочных — на 2–4 пункта, а в двухстрочных и многострочных — сообразно высоте формулы (пример 21).

 

Отдельные части формулы необходимо отбить (отделить) одну от другой. Нормальная величина каждого пробела внутри формулы — 2 пункта (при наборе нонпарелью — 1 пункт).

 

Отбивку внутри формул производят в следующих случаях:

 

знаки, выражающие соотношение между левой и правой частями формулы (=,?, >,<), знаки действий (+,?,?,•,:), знаки геометрических образов (L,?), а также сокращенные обозначения тригонометрических функций и других математических терминов отделяют пробелом как от предыдущей, так и от последующей частей формулы; знак извлечения корня (радикал) отбивают только от предшествующей части формулы, не отделяя его от подкоренного выражения. Знак препинания, помещенный после формулы, не отделяется от нее.

 

 

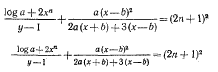
Пример 20

Наборное оформление формулы, часть которой

однострочная, а часть — двухстрочная

 

 

Пример 21

Наборное оформление формулы со знаками

суммы и интеграла

 

Цифры и буквенные обозначения величин, следующие одни за другими и не разделенные какими-либо знаками, не отделяются друг от друга; индексы и показатели степени тоже не отбиваются от тех элементов формулы, к которым они относятся.

 

В двухстрочном выражении (дроби) делительная линейка должна быть равна более длинной части дроби (числителю или знаменателю); более короткая часть дроби выключается на середину по отношению к формату этой линейки.

 

Делительная линейка в дроби должна приходиться против средней линии формулы, то есть против середины знаков =, + и т. п. в однострочной части формулы.

 

Трехстрочное выражение — это дробь, у которой либо числитель, либо знаменатель тоже дробный. Чтобы читатель мог сразу отличить основную дробь от вспомогательной (то есть от той, которая служит числителем или знаменателем основной дроби), делительная линейка основной дроби выделяется либо увеличенной длиной (на 4—8 пунктов длиннее линейки вспомогательной дроби), либо повышенной жирностью. Аналогичный способ применяется и для четырехстрочных выражений.

 

Формулы, расположенные отдельными строками, обычно выключают в красную строку, то есть на середину формата (при асимметричном расположении некоторых других элементов, например заголовков, и формулы могут быть выключены таким же образом).

 

Формула, которая расположена в подбор с текстом, обязательно отделяется достаточно заметным пробелом (не менее половины кегля шрифта) от предшествующего и следующего за ней текста.

 

Переносы в формулах нежелательны. Чтобы уместить формулу в формат строки и таким образом избежать переноса, можно уменьшить пробелы между элементами.

 

Если таким путем не удается довести длинную формулу до формата строки, то перенос делается в первую очередь на знаках соотношения между левой и правой ее частями (=, =, >, <); во вторую — на знаках сложения или вычитания (+, -), делящих формулу на члены; в третью — на знаке умножения (х), который для этой цели вводится в математическое выражение. При переносе нельзя разделять особенно тесно связанные между собой элементы формулы — дроби, выражения в скобках, а также выражения, относящиеся к знакам радикала, интеграла, суммы и произведения.

 

Если в дроби числитель или знаменатель не умещается в одну строку, можно применить один из следующих способов:

набрать дробь шрифтом пониженного кегля;

набрать числитель в две строки с переносом, поместив обе строки над линейкой (или знаменатель в две строки с переносом, поместив их под линейкой) (пример 22);

преобразовать дробь, представив ее в виде суммы или произведения двух дробей, вторую из которых переносят в следующую строку; такое преобразование сравнительно несложно, но сделать его имеет право только автор или редактор.

 

Первый способ применим, если длина дроби лишь не намного превышает формат строки. Второй — особенно уместен, если переносимая часть дроби (числитель или знаменатель) не громоздка и в ней нет знаков радикала, интеграла и т. п. Третий — хорош при условии, что новая форма дроби будет вполне понятна читателю.

 

Вопрос о том, какой из перечисленных способов выбрать, должен быть согласован с редактором.

 

Во всех случаях переноса его знак повторяют два раза — в конце первой строки и в начале второй. Таким образом связь между обеими строками делается особенно заметной; благодаря этому читателю становится легче сразу охватить формулу глазом.

 

Переносимая формула может быть расположена двумя способами: по первому способу обе части (обе строки) формулы выключаются в красную строку; по второму же способу начало (первая строка формулы) выключается к левому краю формата или с небольшим отступом от него, а переносимая часть (вторая строка формулы) — к правому краю или с таким же отступом от него (пример 23).

 

При втором способе связь между обеими частями формулы более заметна.

 

Описанная система наборного оформления математических формул облегчает их восприятие, но некоторые положения ее приводят к тому, что формулы занимают довольно много места. Так, если формула (или какая-нибудь часть ее) представляет собой дробь, у которой знаменатель расположен под числителем и отделен от него горизонтальной чертой, то она (формула) занимает по высоте не одну строку, а немного больше двух; такую формулу нельзя набирать в подбор, а приходится помещать вразрез полосы и отбивать от предшествующего и последующего текста. В результате формула-дробь займет примерно четыре строки.

 

Разработаны некоторые изменения системы, позволяющие более экономно использовать площадь бумаги. Важнейшее из них заключается в том, что в дробях знаменатель располагается не под числителем, а в одной строке с ним и отделяется от него косой чертой.

 

При этом двухстрочная формула превращается в однострочную; знаки?,? и? в однострочных формулах набирают шрифтом того же кегля, что и основную строку.

 

Пример 22

Наборное оформление трехстрочной математической формулы

 

 

Пример 23

Наборное оформление формулы c переносом

 

В таком виде формула не только занимает одну строку вместо двух, но и может быть помещена в подбор с текстом, а не выделена в отдельную строку.

 

Подобные приемы дают экономию бумаги, но затрудняют восприятие формул недостаточно подготовленным читателем. Поэтому они могут быть использованы в монографиях и статьях для специалистов, но их не применяют в учебниках.

Химические формулы

 

Химические формулы оформляются во многом по тем же правилам, что и математические: кегль основных строк равен кеглю окружающего текста; для обозначения валентности — такие же кегль и расположение, как для индексов в математических формулах; для сокращенных наименований химических элементов используется тоже прямой шрифт; так же отделяются математические знаки и знаки связи.

 

Вместе с тем наборное оформление химических формул имеет и свои особенности.

 

Знаки электрических зарядов (+, ",, ') могут быть помещены либо справа от обозначения элемента, либо над ним. Первый способ технически проще и потому применяется чаще. Второй предпочтителен, если необходимо сжать формулу по ширине.

 

Под формулой химического соединения может быть помещено его наименование, которое набирают прямым шрифтом пониженного кегля (лучше всего, для компактности, кг. 6) и выключают на середину формулы, без отбивки.

 

Надо различать точку как знак связи (она располагается на средней линии строки) и как знак, разделяющий сложное соединение на менее сложные группы (в таких случаях точка должна быть расположена на нижней линии строки).

 

Наиболее сложно наборное оформление структурных формул — как открытых, так и кольцевых.

 

Открытая структурная формула может быть вытянута по вертикали или по горизонтали, во многих случаях может быть построена с помощью как прямых, так и косых знаков связи (пример 24).

 

Формула, вытянутая по горизонтали, обычно занимает меньше места на странице. При таком расположении яснее выражена свойственная многим формулам симметричность, которая облегчает и понимание, и запоминание структуры того или иного вещества. Вместе с тем и вертикальный вариант имеет свои достоинства — в этом случае можно точно показать, через атомы каких элементов осуществляется связь. Все же чаще отдают предпочтение горизонтальному варианту.

 

 

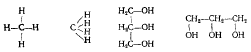
Пример 24

Наборное оформление открытой структурной формулы

 

Для лучшего понимания структурной формулы необходимо, чтобы ее однородные части набирались единообразно, в частности знаки связи в таких случаях имели одинаковую длину. Нормальная длина знаков связи — кегль шрифта, которым набрана формула; более длинные знаки связи оправданы только в тех случаях, когда это вызывается особенностями построения формулы. Знаки связи должны одинаково примыкать к середине буквы (по высоте или по ширине) и одинаково отстоять от буквы, с какой бы стороны они ни примыкали к ней.

 

В некоторых структурных формулах бывает необходимо выделить часть формулы или подчеркнуть значение связи между теми или другими элементами. В таких случаях основную часть формулы выделяют штриховкой, знаки связи изображают более жирной линией (пример 25).

 

Большое значение имеет компактность структурных формул. Она не только позволяет уменьшить объем издания, но и облегчает чтение — формулу, занимающую меньше места, легче охватить глазом. Для достижения компактности в структурных формулах целесообразно набирать буквенные обозначения химических элементов шрифтом кг. 8, если даже текст набран кг. 10 (эти буквенные обозначения в большой мере состоят из прописных букв, которые и в кг. 8 имеют достаточно крупное очко). При снижении кегля шрифта уменьшается и длина знаков связи. Если в издании для структурных формул применен шрифт кг. 8, то и остальные химические формулы, выделенные в отдельную строку, набираются этим же кеглем.

 

Рекомендуется набирать структурные формулы с помощью специальной системы наборных знаков «Химия». Входящие в эту систему знаки имеют минимально необходимые размеры, что дает заметную экономию бумаги. Она включает знаки, позволяющие набирать формулы с изогнутыми и перекрещивающимися линиями связи, с буквенными и цифровыми обозначениями, которые расположены внутри образованного линиями связи угла, и т. п. При старом ассортименте знаков набор таких формул был невозможен; их приходилось вычерчивать от руки и полученный таким путем оригинал клишировать; такой способ и трудоемок, и дорог, и замедляет выпуск издания. Все входящие в систему знаки строго координированы по размеру. Благодаря этому набор получается достаточно плотным, исключается вырывание отдельных знаков при печатании (а следовательно, и появление опечаток).

 

 

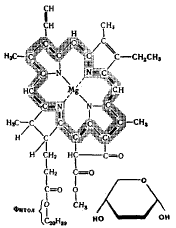
Пример 25

Выделение в структурной формуле

 

Если в типографии нет наборного материала «Химия» и клиширование сложной структурной формулы неизбежно, то ее оригинал следует подготовлять так, чтобы оттиск возможно меньше отличался от наборного. Для этого прежде всего необходимо выполнить оригинал с расчетом на такое уменьшение, при котором на отпечатке толщина штрихов, а также размер букв и цифр в набранных и клишированных формулах были бы одинаковы. Кроме того, буквы и цифры на оригинале должны быть той же шрифтовой гарнитуры, какая применяется в данном издании для набора остальных структурных формул.

 

Логически правильное построение таблиц, правильное и четкое написание, а во многих случаях и целесообразное преобразование математических и химических формул являются необходимым предварительным условием их доброкачественного наборного оформления.

Иллюстрирование книги

 

 

Все ли можно выразить словом?

А. А. Сидоров

 

Иллюстрации — существенный элемент многих изданий, принадлежащих к самым различным видам литературы. При этом разнообразен и сам изобразительный материал, различны задачи его оформления, назначение иллюстраций, различна их связь с текстом. Особенно заметна вся глубина этих различий, если сравнить иллюстрации к произведениям научно-познавательной и художественной литературы.

Иллюстрирование научно-познавательной книги

Задачи и план иллюстрирования

 

Как в процессе создания научно-познавательного произведения, так и в процессе понимания его при чтении основную роль играет логическое мышление, разум.

 

Благодаря своей наглядности иллюстрации к такому произведению значительно облегчают понимание текста. Во многих случаях иллюстрации способны графическими средствами передавать содержание яснее, чем это можно сделать словами, и поэтому в той или иной мере заменяют текст. Таким образом, иллюстрации к произведению научно-познавательной литературы всегда очень тесно связаны с его текстом и очень часто являются неотъемлемой, равноправной (наряду с текстом) частью этого произведения. А в некоторых научно-познавательных изданиях иллюстрациям принадлежит даже доминирующая роль.

 

За последние десятилетия благодаря успехам полиграфической техники воспроизведение иллюстраций, в том числе и многокрасочных, стало и проще, и дешевле. Иллюстрации стали занимать большее место в книге, особенно в учебной, справочной. И все же вопросам иллюстрирования познавательной книги еще далеко не всегда уделяется достаточное внимание. Нередко автор считает себя ответственным лишь за текст, а для иллюстрирования дает тот материал, который был у него «под рукой», не особенно заботясь о его познавательной ценности, наглядности и технической пригодности. Да и редактор часто уделяет основное внимание литературному материалу, не задумываясь над иллюстрационным. Вот почему в иллюстрировании многих книг нет последовательно проведенной системы.

 

Важно, чтобы иллюстрирование научно-познавательной книги велось по определенному плану, с единым (но, конечно, не механическим) подходом к иллюстрированию всех ее частей. Этот принцип далеко не всегда выдерживается, особенно если главы книги написаны разными авторами. Часто приходится видеть в книге разнобой в иллюстрировании аналогичных тем. Так, совершенно однородные описания различных машин иллюстрируются в одном случае чертежом, в другом — фотографией, в третьем — вовсе не иллюстрируются.

 

При редакционной оценке представленных иллюстраций необходимо обращать внимание не только на их тематику, но и на содержательность, на соответствие назначению книги. При недостаточно вдумчивом отношении к иллюстрированию в книге часто отсутствуют нужные иллюстрации и, наоборот, появляются иллюстрации, не несущие полезной информации. Довольно часты случаи, когда в научно-технических изданиях помещают рабочие (производственные) чертежи, на которых показано множество не нужных читателю деталей. Бывает и так, что в книге даны иллюстрации, изображающие лишь общий вид машины, и отсутствуют чертежи, объясняющие ее конструкцию.

 

При обсуждении плана-проспекта будущей книги необходимо договориться с автором и о плане ее иллюстрирования, о характере (а также о приблизительном количестве) предполагаемых иллюстраций. Благодаря такому подходу с самого начала работы над будущей книгой внимание автора будет направлено на подготовку не только текста, но и иллюстрационного материала.

Различия в характере иллюстраций

 

По характеру изображения научно-познавательные иллюстрации можно разделить на предметные и условные.

 

Для предметных иллюстраций весьма характерно видимое сходство с реальным объектом. Именно оно является одним из важнейших условий, определяющих познавательную ценность изображения. Конечно, любое графическое изображение в той или иной мере условно, но стремление преодолеть или хотя бы ограничить эту условность характерно для предметного изображения.

 

Условное изображение, наоборот, не показывает объект (явление) во всей полноте конкретных признаков, а лишь характеризует его с определенной стороны. Видимое сходство между реальным объектом и его условным изображением очень часто невелико, а то и вовсе отсутствует. Например, чертеж, показывающий конструкцию машины, не похож на нее «в натуре». Однако отсутствие видимого сходства с реальным объектом не лишает условное изображение научно-познавательной ценности. Наоборот, благодаря абстрагированию от всего несущественного (с точки зрения той цели, для которой помещается в книге данная иллюстрация), такое изображение может особенно полно и точно передавать существенную информацию об объекте или явлении.

 

Основными видами предметных научно-познавательных изображений являются фотография и рисунок. К условным относятся чертежи, схемы, диаграммы, карты.