Расчет и выбор переходных посадок

Сопряжение конической шестерни с валом является неподвижным, разъемным. Неподвижность достигается наличием шпонки. При таком соединении целесообразно применить посадку . Это наиболее приме­няемый тип посадок. Вероятность получения зазоров и натягов в соедине­нии примерно одинакова. Сборка и разборка производится без значитель­ных усилий. Небольшой натяг достаточен для центрирования деталей и предотвращения вибраций.

Применяем посадку Ø18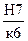

Рисунок 1.3 – Схема расположения полей допусков посадки Ø18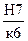

Определяем наименьшее d_min и D_min, средние d_ср и D_ср, наибольшие d_max и D_max диаметры для вала и отверстия соответственно, мм:

(1.14)

где d_н и D_н – номинальные размеры вала и отверстия соответственно, мм;

EI – нижнее отклонение поля допуска отверстия, мм;

ei - нижнее отклонение поля допуска вала, мм;

ES – верхнее отклонение поля допуска отверстия, мм;

es – верхнее отклонение поля допуска вала, мм;

TD– допуск отверстия, мм.

Td – допуск вала, мм.

 

Вычисляем допуски отверстия и вала, мм:

(1.15)

TD = 0,021 – 0 = 0,021

Td = 0,012 – 0,002 = 0,010

Вычисляем диаметры отверстия и вала, мм:

D_min = 18 + 0 = 18

D_ср = 18 + = 18,0105

D_max = 18 + 0,021 = 18,021

d_min = 18 + 0,002 = 18,002

d_ср = 18 + = 18,005

d_max = 18 + 0,012 = 18,012

Определяем максимальный натяг N_max, мкм, и максимальный зазор S_max,мкм:

(1.16)

N_max = 12 – 0 = 12

S_max = 21 – 2 = 19

Расчет вероятности распределения натягов и зазоров с доверительной вероятностью 0,9973.

Предположим, что погрешности изготовления сопрягаемых деталей подчиняются закону нормального распределения, а центр их группирования совпадает с полем допуска, TD и Td, мкм. Определяем среднеквадратическое отклонение размеров сопрягаемых деталей σ_D и σ_d, мкм:

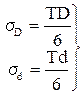(1.17)

Находим суммарное среднеквадратическое отклонение, мкм:

(1.18)

Определим величину среднего зазора S_ср, мм:

S_ср = D_ср - d_ср (1.19)

S_ср = 18,0105 – 18,005 = 0,01

S_ср определяет положение центра группирования относительно начала их отсчета x = S_ср. На оси х-х эта точка обозначается х’ = 0. Она отделяет зазор от натяга.

На оси z-z эта точка определяется:

, (1.20)

,

где z – является пределом интегрирования интеграла функции Лапласа.

Определяем относительное количество соединений с зазором S_%:

S_% = (Ф_{0 (0,9375)} + 0,5)·100% (1.21)

где Ф_{0 (0,9375)} – значение функции Лапласа при z = 0,9375 [1, с.12]

S_% = (0,325 + 0,5)·100% = 82,5

Найдем фактическое значение наибольших зазоров S_max, мкм, и натягов N_max, мкм

(1.22)

S_max = 3 · 3,8 + 4,5 = 15,9

N_max = 3 · 3,8 – 4,5 = 6,9

Строим кривую распределения зазоров и натягов. Уравнение кривой имеет вид

(1.23)

где y – плотность вероятности;

х – аргумент функции и плотности вероятности;

σ – среднеквадратическое отклонение случайных величин, мкм.

 

Таблица 1.1 – Зависимость плотности вероятности у от аргумента х

х		σ	2σ	3σ	0,84σ
у	0,09	0,047	0,01	0,0007	0,059

 

Рисунок 1.4 – Кривая распределения зазоров и натягов.