„асто при расчетах, проводимых по различным финансовым операци€м, возникает необходимость в определении эквивалентных процентных ставок.
Ёквивалентные процентные ставки Ч это такие процентные ставки разного вида, применение которых при различных начальных услови€х дает одинаковые финансовые результаты.
Ёквивалентные процентные ставки необходимо знать в случа€х, когда существует возможность выбора условий финансовой операции и требуетс€ инструмент дл€ корректного сравнени€ различных процентных ставок.
ƒл€ нахождени€ эквивалентных процентных ставок используют уравнени€ эквивалентности, принцип составлени€ которых заключаетс€ в следующем. ¬ыбираетс€ величина, которую можно рассчитать при использовании различных процентных ставок (обычно это наращенна€ сумма S). Ќа основе равенства двух выражений дл€ данной величины составл€етс€ уравнение эквивалентности, из которого путем соответствующих преобразований получаетс€ соотношение, выражающее зависимость между процентными ставками различного вида.
–ассмотрим случай, когда все услови€ финансовой операции совпадают, т. е. первоначальный капитал, временна€ база, метод расчета (точный или обыкновенный) процентов и период начислени€ одинаковы. ¬ противном случае примен€ютс€ те же рассуждени€ и преобразовани€, только полученные формулы будут содержать несколько большее количество переменных. ¬спомним обозначени€, использованные ранее:
Ø i Ч проста€ годова€ ставка ссудного процента;
Ø d Ч проста€ годова€ учетна€ ставка;
Ø ic Ч сложна€ годова€ ставка ссудного процента;
Ø dc Ч сложна€ годова€ учетна€ ставка;
Ø j Ч номинальна€ ставка ссудного процента;
Ø f Ч номинальна€ учетна€ ставка.
ѕовторим формулы дл€ определени€ наращенной суммы при различных способах начислени€ процентов, полученные в предыдущих параграфах этой главы:
| 1.7 | 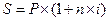
|
| 2.5 | 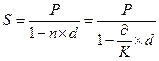
|
| 3.1 | 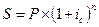
|
| 3.6 | 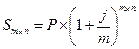
|
| 4.1 | 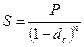
|
| 4.5 | 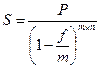
|
ѕриравнива€ эти формулы попарно, можно получить соотношени€, выражающие зависимость между любыми двум€ различными процентными ставками.
–ассмотрим несколько случаев.
ѕриравнива€ соотношени€ (1.7) и (2.5), получим: 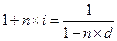 .
.
ќткуда
| 5.1 | 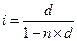
|
| 5.2 | 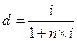
|
»з формул (1.7) и (3.1) имеем: 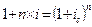
| 5.3 | 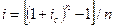
|
| 5.4 | 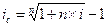
|
ѕриравнивание формул (1.7) и (3.6) дает: 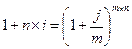
| 5.5 | 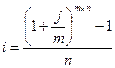
|
| 5.6 | 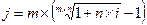
|
ƒл€ различных случаев сложных процентов получаем уравнение эквивалентности, приравнива€ формулы (3.1) и (3.6): 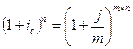
| 5.7 | 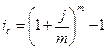
|
| 5.8 | 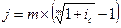
|
ѕолученна€ по формуле (5.7) годова€ ставка сложных процентов, эквивалентна€ номинальной процентной ставке, называетс€ эффективной ставкой сложных процентов.
Ёффективную ставку сложных процентов полезно знать, чтобы оценить реальную доходность финансовой операции, или сравнить процентные ставки в случае, когда используютс€ различные интервалы начислени€. ќчевидно, что значение эффективной процентной ставки больше значени€ номинальной, а совпадают они при т = 1.
ƒалее из формул (3.1) и (4.1) имеем: 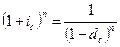
| 5.9 | 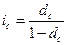
|
| 5.10 | 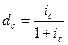
|
јналогичным образом получаем зависимости между любыми другими эквивалентными процентными ставками.
|
|
|
»спользу€ дл€ вычислений формулы (3.1) и (4.1), можно построить таблицу, отражающую зависимость между эквивалентными сложными учетными ставками и ставками ссудных процентов (табл. 5.1). ¬идно, что небольшие учетные ставки имеют эквивалентные ставки ссудного процента, сопоставимые по величине, но с ростом учетных ставок разница увеличиваетс€ очень быстро.
“аблица 5.1. «ависимость между эквивалентными сложными учетными ставками dc(%) и ставками ссудных процентов ic(%)
| dc(%) | ic(%) | Dc(%) | ic(%) |
| 5% | 5,26% | 50% | 100% |
| 6% | 6,4% | 60% | 150% |
| 8% | 8,7% | 70% | 233% |
| 10% | 11% | 80% | 200% |
| 20% | 25% | 85% | 567% |
| 30% | 43% | 90% | 900% |
| 40% | 66,7% | 95% | 1900% |
| 45% | 82% | 99% | 9900% |






