Удельный заряд электрона
Методические указания
К лабораторной работе № 3.10p
по курсу физики для студентов дневной и заочной форм
обучения всех технических специальностей
Владивосток 2009
Одобрено научно-методическим советом университета
УДК 53.082.1; 531.76
И88
Удельный заряд электрона: метод. указания/сост. В.В. Зауткин. – Владивосток: Изд-во ДВГТУ, 2009. – 8с.
В методических указаниях рассмотрено движение в магнитном поле электронного пучка, формируемого электронной пушкой, помещенной в баллон с аргоном при низком давлении. Атомы аргона ионизируются при столкновении с электронами вдоль траектории движения электронов, что заставляет атомы излучать свет. По параметрам траектории, которая становится визуально наблюдаемой, определяется удельный заряд электрона.
Печатается с оригинал-макета, подготовленного автором
 |
Типография ДВГТУ, 690950 Пушкинская, 10
Лабораторная работа №67
Удельный заряд электрона.
Цель работы: экспериментальное определение удельного заряда электрона по
траектории пучка электронов в магнитном поле.
Постановка задачи
Отношение заряда электрона к его массе, называемое удельным зарядом электрона, можно определить, наблюдая траекторию движения электрона, искривленную магнитным полем. Еще из школьного курса физики известно, что на заряженную частицу, движущуюся в магнитном поле, действует сила, называемая силой Лоренца:
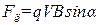, (1)
которая перпендикулярна вектору скорости частицы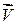 
, направлению индукции магнитного поля 
и по модулю зависит от угла 
между этими векторами. Для определения ее направления известно школьное "правило левой руки", но для студента, знакомого с векторной алгеброй, совершенно очевидно, что выражение (1) есть модуль векторного произведения
, (2)
которое полностью отражает все особенности этой силы (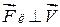
, 
).
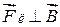Для электрона, имеющего заряд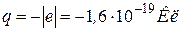 
, сила Лоренца, соответственно равная
, (3)
направлена так, как изображено на рис.1 (где крестики показывают направление силовых линий индукции магнитного поля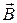 
).
Если электрон движется перпендикулярно полю, то сила Лоренца по модулю равна
. (4)
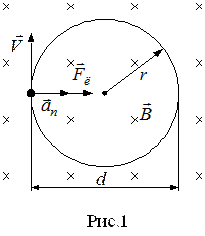Так как сила Лоренца перпендикулярна направлению движения (скорости 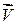), то она не совершает работы, и, следовательно, не изменяет кинетической энергии частицы. Это значит, что частица движется со скоростью, не изменяющейся по величине. Под действием силы Лоренца меняется лишь направление скорости частицы, т.е. траектория искривляется. Иными словами, у частицы нет касательного ускорения 
, но есть нормальное (центростремительное) ускорение, равное, как известно,
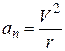, (5)
где r – радиус кривизны траектории.
Записывая уравнение движения (II закон Ньютона)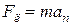 
с учетом (4) и (5) получаем выражение
, (6)
которое определяет радиус кривизны траектории
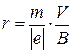. (7)
Так как скорость V не изменяется по величине, то в однородном магнитном поле (
) радиус кривизны всюду одинаков, и следовательно, электрон движется по окружности, радиус которой равен r (7), а диаметр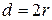 
:
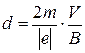. (8)
Зная скорость электрона и определив на опыте диаметр круговой траектории, а также индукцию магнитного поля, легко найти искомую величину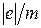 
- удельный заряд электрона
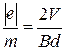. (9)
В этом и состоит главная идея лабораторной работы.
