Электричество
● Сила взаимодействия F между двумя неподвижными точечными зарядами q 1 и q 2 вычисляется по закону Кулона:
F = k∙│q1│∙│q2│/ r2,
где k - коэффициент пропорциональности, r – расстояние между зарядами.
● Напряженность электрического поля – это силовая характеристика, определяемая силой, действующей на единичный точечный положительный заряд q0, помещенный в данную точку поля:
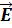 =
= 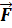 /q0.
/q0.
Линии напряженности электрического поля начинаются на положительных зарядах и заканчиваются на отрицательных зарядах или уходят в бесконечность, то есть силовые линии разомкнуты.
● По теореме Гаусса поток вектора напряженности электрического поля через замкнутую поверхность равен алгебраической сумме зарядов, заключенных внутри поверхности, делённой на электрическую постоянную и диэлектрическую проницаемость среды.
● Напряженность электрического поля равна градиенту потенциала, взятому с обратным знаком:
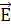 = - grad φ.
= - grad φ.
Связь между проекцией напряженности электрического поля на ось x и потенциалом даётся уравнением:
Ех = - d φ/dx.
● Электростатическое поле является потенциальным. Работа в потенциальном поле сил может быть представлена как разность потенциальных энергий или как произведение заряда q на разность потенциалов:
А = W1 – W2 = q(φ1 – φ2 ).
● По закону Ома для однородного участка цепи:
R = U/I,
где U – напряжение на участке цепи, I – сила тока в цепи, R –сопротивление участка цепи.
Сопротивление однородного проводника:
R = ρ∙ℓ/ S,
где ρ –удельное сопротивление проводника, ℓ- длина участка проводника, S – площадь поперечного сечения.
● Зависимость плотности тока ј от напряженности электрического поля E подчиняется закону Ома в дифференциальной форме:
ј = σ · E,
где σ – удельная проводимость. Удельной проводимостью называется величина, обратная удельному сопротивлению:
σ = 1/ ρ.
● Мощность постоянного тока N равна произведению силы тока I на напряжение U:
N = I·U.
● Закон Ома для полной цепи:
ε = I∙R + I·r,
где ε – ЭДС источника тока, I – сила тока в цепи, R – внешнее сопротивление, r – внутреннее сопротивление источника тока.
Тест 2 -1
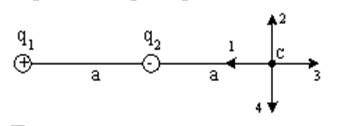
Электрическое поле создано одинаковыми по величине точечными зарядами q1 и q2. Если q1 = +q, q2 = -q, a расстояние между зарядами и от заряда q2 до точки С равно а, то вектор напряженности поля в точке С ориентирован в направлении...
 Варианты ответов:
Варианты ответов:
1) в направлении 1;
2) в направлении 2;
3) в направлении 3;
4) в направлении 4.
Решение.
Напряженность электрического поля – это силовая характеристика, определяемая силой, действующей на единичный точечный положительный заряд, помещенный в данную точку поля: 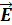 =
= 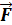 / q0. Для того чтобы определить направление вектора напряженности, надо в данную точку поля (точку наблюдения) поместить воображаемый единичный положительный заряд, тогда вектор силы, действующий на него, укажет направление вектора напряженности. Следовательно, со стороны заряда +q 1 на пробный заряд +q 0, помещенный в точку С, будет действовать сила отталкивания, и вектор напряженности
/ q0. Для того чтобы определить направление вектора напряженности, надо в данную точку поля (точку наблюдения) поместить воображаемый единичный положительный заряд, тогда вектор силы, действующий на него, укажет направление вектора напряженности. Следовательно, со стороны заряда +q 1 на пробный заряд +q 0, помещенный в точку С, будет действовать сила отталкивания, и вектор напряженности 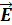 1 будет иметь направление 3, а со стороны отрицательного заряда -q 2 будет действовать сила притяжения, и вектор
1 будет иметь направление 3, а со стороны отрицательного заряда -q 2 будет действовать сила притяжения, и вектор 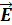 2 будет иметь направление 1. Результирующая напряженность находится по принципу суперпозиции:
2 будет иметь направление 1. Результирующая напряженность находится по принципу суперпозиции:
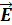 =
= 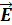 1 +
1 + 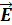 2 . В скалярной форме: E = E 1 - E 2. Модуль вектора напряженности электрического поля точечного заряда равен:
2 . В скалярной форме: E = E 1 - E 2. Модуль вектора напряженности электрического поля точечного заряда равен:
E = k∙q /r2,
где k - коэффициент пропорциональности r – расстояние от точечного заряда до точки наблюдения. Так как расстояние от заряда q1 до точки С в два раза больше, чем от заряда q2, то E 1 < E 2, и вектор E результирующей напряженности электрического поля будет ориентирован в направлении 1.
Ответ: вариант 1.
Тест 2 – 2
Точечный заряд +q находится в центре сферической поверхности. Если добавить заряд +q за пределами сферы, то поток вектора напряженности электростатического поля 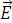 через поверхность сферы...
через поверхность сферы...
Варианты ответов:
1) не изменится; 2) увеличится; 3) уменьшится.
Решение
По теореме Гаусса в вакууме поток вектора напряженности электрического поля через замкнутую поверхность равен алгебраической сумме зарядов, заключенных внутри поверхности, делённой на электрическую постоянную. Поэтому, если добавить заряд за пределами сферы, то поток вектора напряженности электрического поля через поверхность сферы не изменится.
Ответ: вариант 1.
Тест 2 – 3
Точечный заряд +q находится в центре сферической поверхности. Если внутрь сферы добавить заряд - q, то поток вектора напряженности электростатического поля 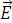 через поверхность сферы...
через поверхность сферы...
Варианты ответов:
1) не изменится; 2) увеличится; 3) уменьшится.
Решение
По теореме Гаусса в вакууме поток вектора напряженности электрического поля через замкнутую поверхность равен алгебраической сумме зарядов, заключенных внутри поверхности, делённой на электрическую постоянную. Если добавить внутрь сферы к положительному заряду q такой же отрицательный заряд, то заряд, заключенный внутри поверхности сферы, станет равным нулю. Поэтому поток вектора напряженности электрического поля станет равным нулю, так как алгебраическая сумма зарядов, заключенных внутри сферы будет равна нулю. Следовательно, поток вектора напряженности электростатического поля 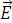 через поверхность сферы уменьшится.
через поверхность сферы уменьшится.
Ответ: вариант 3.
Тест 2 – 4
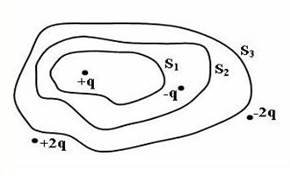 Дана система точечных зарядов в вакууме и замкнутые поверхности S1, S2 и S3. Поток вектора напряженности электростатического поля равен нулю через...
Дана система точечных зарядов в вакууме и замкнутые поверхности S1, S2 и S3. Поток вектора напряженности электростатического поля равен нулю через...
Варианты ответов:
1) поверхность S2;
2) поверхность S3;
3) поверхности S2 и S3;
4) поверхности S1, S2 и S3.
Решение.
По теореме Гаусса в вакууме поток вектора напряженности электрического поля через замкнутую поверхность равен алгебраической сумме зарядов, заключенных внутри поверхности, делённой на электрическую постоянную. Поэтому поток вектора напряженности электрического поля равен нулю через поверхности S2 и S3 т.к. алгебраическая сумма зарядов, заключенных внутри этих поверхностей, равна нулю.
Ответ: вариант 3.
Тест 2 – 5
Относительно статических электрических полей справедливы утверждения:
1) Электростатическое поле совершает работу над электрическим зарядом.
2) Силовые линии поля разомкнуты.
3) Электростатическое поле является вихревым.
Решение.
Проанализируем правильность утверждений.
1. Электростатическое поле является потенциальным. Работа в потенциальном поле сил может быть представлена как разность потенциальных энергий или как произведение заряда на разность потенциалов: А = W1 – W2 = q(φ1 – φ2 ). Поэтому первое утверждение является верным, т.е. электрическое поле совершает работу над электрическим зарядом.
2. Линии напряженности электрического поля начинаются на положительных зарядах и заканчиваются на отрицательных зарядах или уходят в бесконечность, то есть силовые линии разомкнуты. Поэтому второе утверждение также является верным.
3. Третье утверждение является неверным. Вихревое поле имеет замкнутые линии, но оно создается только переменным полем, а не статическим.
Ответ: справедливы утверждения 1 и 2.
Тест 2 – 6
На рисунке показаны эквипотенциальные линии системы зарядов и значения потенциала на них. Вектор напряженности электрического поля в точке А ориентирован в направлении...
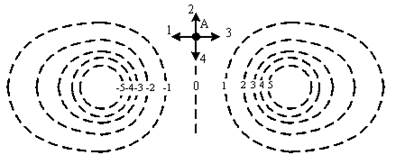
Варианты ответов: 1) в направлении 1; 3) в направлении 3;
2) в направлении 2; 4) в направлении 4.
Решение.
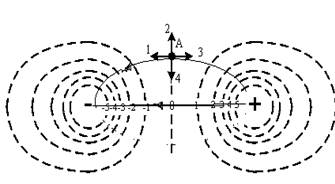 Потенциал поля, созданного электрическим зарядом, зависит от знака этого заряда. Если значения потенциала эквипотенциальных линий являются отрицательными, то это означает, что поле создано отрицательным зарядом и наоборот, если эти значения положительные, то поле создано положительным зарядом. Линии напряженности электрического поля начинаются на положительном заряде, заканчиваются на отрицательном заряде или уходят в бесконечность. Вектор напряженности электрического поля направлен по касательной к линии напряженности.
Потенциал поля, созданного электрическим зарядом, зависит от знака этого заряда. Если значения потенциала эквипотенциальных линий являются отрицательными, то это означает, что поле создано отрицательным зарядом и наоборот, если эти значения положительные, то поле создано положительным зарядом. Линии напряженности электрического поля начинаются на положительном заряде, заканчиваются на отрицательном заряде или уходят в бесконечность. Вектор напряженности электрического поля направлен по касательной к линии напряженности.
На рисунке в решении изображена линия напряженности, проходящая через заданную точку А. Вектор напряженности электрического поля ориентирован по касательной к этой линии, т.е. в направлении 1.
Ответ: направление 1.
.
Тест 2 – 7
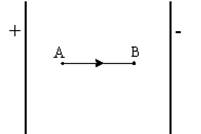
В электрическом поле плоского конденсатора перемещается заряд + q в направлении, указанном стрелкой. Тогда работа сил поля на участке АВ...
 Варианты ответов:
Варианты ответов:
1) 1) отрицательна;
2) 2) равна нулю;
3) 3) положительна.
Решение.
В плоском конденсаторе линии напряженности электрического поля представляют собой прямые, параллельные участку АВ, которые начинаются на положительной и заканчиваются на отрицательной обкладке конденсатора. Сила, действующая на электрический заряд, равна: 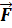 = q
= q 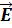 . Работа постоянной силы равна: A = F·∆S· cos α = q E ·∆S· cos α, где ∆S – модуль перемещения, α – угол между направлением силы и направлением перемещения. В данном случае α = 0, cos 0˚= 1 и работа сил поля на участке АВ больше нуля (A> 0).
. Работа постоянной силы равна: A = F·∆S· cos α = q E ·∆S· cos α, где ∆S – модуль перемещения, α – угол между направлением силы и направлением перемещения. В данном случае α = 0, cos 0˚= 1 и работа сил поля на участке АВ больше нуля (A> 0).
Ответ: вариант 3.
Тест 2 – 8
На рисунке представлены графики, отражающие характер зависимости поляризованности Р диэлектрика от напряженности поля Е. Укажите зависимость, соответствующую неполярным диэлектрикам.
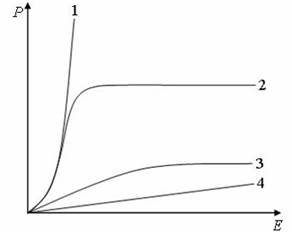
Варианты ответов:
1) 1) График 2;
2) 2) График 3;
3) 3) График 4;
4) 4) График 1.
Решение.
Для большого класса диэлектриков (за исключением сегнетоэлектриков и пьезоэлектриков) зависимость поляризованности Р от напряженности электрического поля Е имеет вид: Р = χ ·ε0 ·Е, где χ – диэлектрическая восприимчивость, характеризующая свойства диэлектрика, ε 0 – электрическая постоянная. Для диэлектриков, построенных из неполярных молекул, диэлектрическая восприимчивость χ постоянна при любых значениях Е и мала по абсолютной величине. Для диэлектриков, построенных из полярных молекул, при небольших значениях напряженности электрического поля зависимость Р(Е) линейная, а при больших значениях Е наблюдается насыщение и χ становится равным единице. Поэтому зависимость поляризованности Р от напряжённости электрического поля Е, соответствующая неполярным диэлектрикам, является линейной, что на рисунке соответствует прямой 4.
Ответ: вариант3.
Тест 2 – 9
На рисунке представлена зависимость плотности тока  , протекающего в проводниках 1 и 2, от напряженности электрического поля
, протекающего в проводниках 1 и 2, от напряженности электрического поля 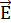 . Отношение удельных проводимостей
. Отношение удельных проводимостей
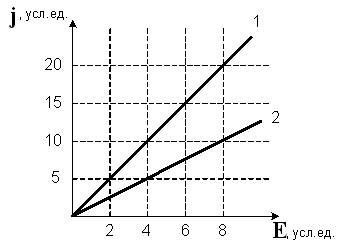 этих элементов σ 1 /σ 2 равно...
этих элементов σ 1 /σ 2 равно...
Варианты ответов:
1) 4;
1) 2) 1/4;
3) 3) 1/2;
4) 2.
Решение.
Зависимость плотности тока от напряженности электрического поля подчиняется закону Ома в дифференциальной форме: ј = σ·E, где σ – удельная проводимость. Заметим, что удельной проводимостью называется величина, обратная удельному сопротивлению: σ = 1/ρ. При постоянном значении напряженности электрического поля, т.е. при Е = const, отношение плотностей токов равно отношению удельных проводимостей: ј1 / ј2=σ1/σ2.
Используя график, найдем отношение удельных проводимостей элементов. Например, при Е = 8 усл. ед. отношение удельных проводимостей равно: σ1/σ 2=20 /10 =2.
Ответ: вариант 4.
Тест 2 – 10
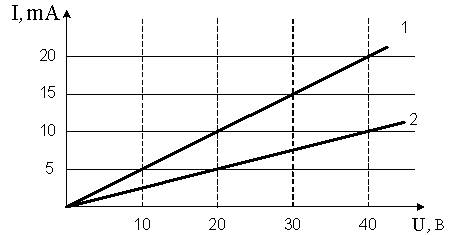 Вольтамперная характеристика активных элементов цепи 1 и 2 представлена на рисунке. На элементе 1 при токе 15 mА выделяется мощность...
Вольтамперная характеристика активных элементов цепи 1 и 2 представлена на рисунке. На элементе 1 при токе 15 mА выделяется мощность...
Варианты ответов:
1) 450 Вт; 2) 0,30 Вт; 3) 0,45 Вт; 4) 15 Вт.
Решение.
Мощность тока равна произведению силы тока на напряжение: N = I·U. Определим по графику, представляющему собой вольт – амперную характеристику, напряжение на элементе 1. При силе тока I = 15 mA напряжение равно U = 30 В. Подставим в формулу численные значения в системе СИ: N = 0.015·30 = 0.45 Вт. Ответ: вариант 3.
Задание С2-7 для самостоятельного решения.
Воспользовавшись тем же графиком теста 2 - 10, определите мощность, выделяющуюся на элементе 2, при напряжении 20 В.
Варианты ответов:
1) 0,5 Вт; 2) 100 Вт; 3) 20 Вт; 4) 0, 1 Вт.
Тест 2 – 11
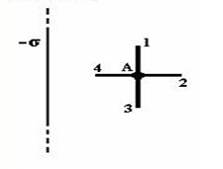 Поле создано бесконечной равномерно заряженной плоскостью с поверхностной плотностью заряда - σ. Укажите направление вектора градиента потенциала в точке А.
Поле создано бесконечной равномерно заряженной плоскостью с поверхностной плотностью заряда - σ. Укажите направление вектора градиента потенциала в точке А.
Варианты ответов:
1) На 1) направление А – 1.
2) На 2) направление А – 3.
3) На 3) направление А – 4.
4) На 4) направление А – 2.
Решение.
Напряженность электрического поля равна градиенту потенциала, взятому с обратным знаком: 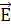 = - grad φ. Так как электрическое поле создано бесконечной отрицательно заряженной плоскостью, то линии напряженности электрического поля перпендикулярно входят в отрицательно заряженную плоскость. Следовательно, вектор напряженности электрического поля имеет направление А – 4, при этом градиент потенциала направлен в противоположную сторону, т.е. имеет направление А – 2.
= - grad φ. Так как электрическое поле создано бесконечной отрицательно заряженной плоскостью, то линии напряженности электрического поля перпендикулярно входят в отрицательно заряженную плоскость. Следовательно, вектор напряженности электрического поля имеет направление А – 4, при этом градиент потенциала направлен в противоположную сторону, т.е. имеет направление А – 2.
Ответ: вариант 4.
Тест 2 – 12
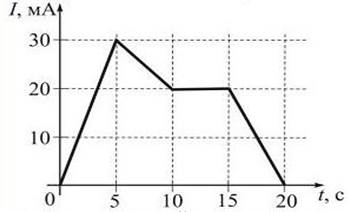
На рисунке показана зависимость силы тока в электрической цепи от времени. Заряд, прошедший по проводнику на интервале времени от 5 до 15 с (в мКл) равен...
 Варианты ответов: Варианты ответов:
Варианты ответов: Варианты ответов:
1) 200; 2) 225;
3) 450; 4) 250.

Решение.
Заряд, прошедший по проводнику на интервале времени от t1 до t2, равен интегралу q = 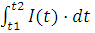 , где I(t) – функция, описывающая зависимость силы тока от времени. Согласно геометрическому смыслу, интеграл численно равен площади фигуры, ограниченной графиком подынтегральной функции и осью абсцисс и двумя ординатами t= t1 и t= t2. Площадь фигуры, изображённой на рисунке, удобно подсчитать как число клеток, умноженное на цену деления одной клетки. На заданном интервале времени от 5 до 15 с число клеток равно 4,5. Цена деления одной клетки 5·10 = 50 мКл /с. Площадь фигуры 4,5·50 = 225, поэтому заряд, прошедший по проводнику, равен 225 мКл.
, где I(t) – функция, описывающая зависимость силы тока от времени. Согласно геометрическому смыслу, интеграл численно равен площади фигуры, ограниченной графиком подынтегральной функции и осью абсцисс и двумя ординатами t= t1 и t= t2. Площадь фигуры, изображённой на рисунке, удобно подсчитать как число клеток, умноженное на цену деления одной клетки. На заданном интервале времени от 5 до 15 с число клеток равно 4,5. Цена деления одной клетки 5·10 = 50 мКл /с. Площадь фигуры 4,5·50 = 225, поэтому заряд, прошедший по проводнику, равен 225 мКл.
Ответ: вариант 2.
Тест 2 – 13
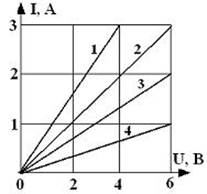 Через лампу, подключенную к источнику тока с ЭДС 8 В и внутренним сопротивлением 1,0 Ом протекает ток 2 А. Зависимость тока от приложенного к лампе напряжения показана на графике …
Через лампу, подключенную к источнику тока с ЭДС 8 В и внутренним сопротивлением 1,0 Ом протекает ток 2 А. Зависимость тока от приложенного к лампе напряжения показана на графике …
Варианты ответов:
1) 2; 2) 4;
3) 1; 4) 3.
Решение.
Согласно закону Ома для полной цепи, имеем: ε = I∙R + I·r, где ε – ЭДС источника тока, I – сила тока в цепи, R – внешнее сопротивление, r – внутреннее сопротивление источника тока. По условию задачи ε = 8 В, I = 2 А, r = 1,0 Ом. Отсюда найдём сопротивление лампы:R = (ε - I·r)/ I = (8-2·1)/2 = 3 Ом. По закону Ома для однородного участка цепи: R = U / I, где U – напряжение на участке цепи. Поэтому отношению U / I =6/2= 3 соответствует график 3.
Ответ: вариант 4.
Тест 2 – 14
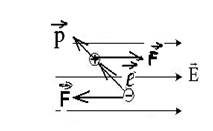
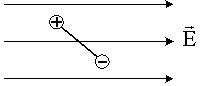 Жесткий электрический диполь находится в однородном электростатическом поле.
Жесткий электрический диполь находится в однородном электростатическом поле.
Момент сил, действующий на диполь, направлен...
Варианты ответов: 1) Против вектора напряженности поля; 2) от нас;
3) Вдоль вектора напряженности поля; 4) к нам.
Решение.
Момент сил, действующих на электрический диполь, равен векторному произведению электрического момента диполя 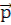 на вектор напряженности электрического поля:
на вектор напряженности электрического поля: 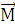 = [
= [ 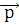 ·
· 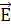 ]. Электрический момент диполя
]. Электрический момент диполя 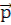 = q∙
= q∙ 
 направлен вдоль оси диполя от отрицательного заряда к положительному. Направление момента сил
направлен вдоль оси диполя от отрицательного заряда к положительному. Направление момента сил 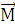 , действующих на диполь, определяется по правилу векторного произведения двух векторов, т.е. это будет вектор, перпендикулярный плоскости, в которой лежат перемножаемые вектора. Направление вектора
, действующих на диполь, определяется по правилу векторного произведения двух векторов, т.е. это будет вектор, перпендикулярный плоскости, в которой лежат перемножаемые вектора. Направление вектора 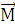 ( к нам или от нас) можно определить по правилу правого винта: если первый вектор поворачивать ко второму, то поступательное движение винта укажет направление векторного произведения. В нашем случае вектор
( к нам или от нас) можно определить по правилу правого винта: если первый вектор поворачивать ко второму, то поступательное движение винта укажет направление векторного произведения. В нашем случае вектор 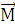 направлен от нас.
направлен от нас.
Этот вывод подтверждает рисунок, на котором показаны силы, вращающие диполь. Очевидно, что под действием этих сил поворот диполя произойдёт по часовой стрелке. Следовательно, поступательное, движение винта будет направлено от нас, т.е. вектор 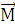 направлен от нас за чертёж.
направлен от нас за чертёж.
Ответ: вариант 2.
Тест 2 – 15
Зависимость удельного сопротивления проводника от температуры в области сверхпроводящего перехода представлена графиком...
Варианты ответов:
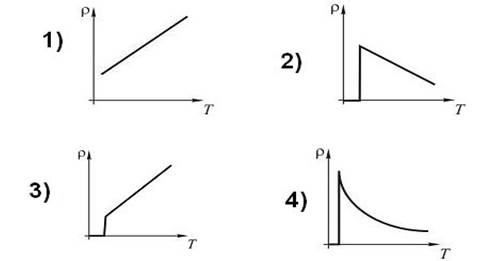
Решение.
Сверхпроводимостью называется явление, при котором при понижении температуры электрическое сопротивление проводника (в том числе удельное сопротивление) скачкообразно обращается в нуль при некоторых критических значениях температуры, характерной для каждого вещества. Следовательно, зависимость удельного сопротивления проводника от температуры в области сверхпроводящего перехода представлена графиком 3. Ответ: вариант 3..
Тест 2 – 16
При помещении полярного диэлектрика в электростатическое поле...
Варианты ответов:
1) В образце индуцируются упругие электрические дипольные моменты атомов, совпадающие по направлению с имевшимися электрическими дипольными моментами молекул; вектор поляризованности образца направлен против направления внешнего поля;
2) происходит ориентирование имевшихся электрических дипольных моментов молекул; вектор поляризованности образца направлен по направлению внешнего поля;
3) происходит ориентирование имевшихся электрических дипольных моментов молекул; вектор поляризованности образца направлен против направления внешнего поля;
4) в образце индуцируются упругие электрические дипольные моменты атомов, компенсирующие имевшиеся электрические дипольные моменты молекул; вектор поляризованности образца остается равным нулю.
Решение
Молекулы полярного диэлектрика в отсутствие внешнего электрического поля обладают электрическим дипольным моментом. Однако, вследствие теплового движения дипольные моменты отдельных молекул ориентированы хаотично и их результирующий момент равен нулю. Если такой диэлектрик поместить во внешнее электрическое поле, то происходит ориентирование электрических дипольных моментов по направлению внешнего поля. Тепловое движение этому препятствует. В результате устанавливается преимущественная ориентация дипольных моментов по полю. Вектор поляризованности, определяемый как дипольный момент единицы объёма диэлектрика, также направлен по направлению внешнего поля.
Ответ: вариант 2.
Тест 2 – 17
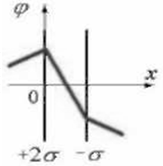 Электрическое поле создано двумя бесконечными параллельными плоскостями, заряженными с поверхностными плотностями + 2σ и - σ. На рисунке показана качественная зависимость проекции напряженности поля Еx от координаты x вне пластин и между пластинами.
Электрическое поле создано двумя бесконечными параллельными плоскостями, заряженными с поверхностными плотностями + 2σ и - σ. На рисунке показана качественная зависимость проекции напряженности поля Еx от координаты x вне пластин и между пластинами.
Правильно отражает качественную зависимость проекции напряженности поля Ех на ось х график...
Варианты ответов:
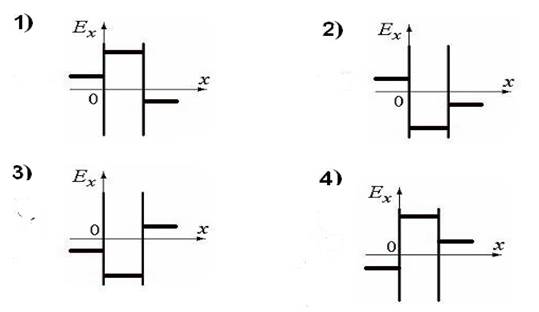
Решение
Как видно из рисунка, на всех трех участках (слева, справа и между заряженными плоскостями) графики зависимости потенциала φ от координаты х представляет собой прямую, уравнение которой можно записать в виде: φ = φ0 ±. Ех·x (знак плюс, если функция возрастает и знак минус, если функция убывает). Связь между проекцией напряженности электрического поля на ось x и потенциалом даётся уравнением: Ех = - d φ/dx. Производная от линейной функции по координате является постоянной величиной, численно равной тангенсу угла наклона прямой к оси х: tgα=Δ φ /Δx = - Ех. Если функция φ(x) возрастает,, то tgα >0 и Ех <0, а если функция φ(x) убывает, то tgα <0 и Ех > 0.
Проанализируем варианты ответов.
На участке слева от заряженных плоскостей фукция φ(x) возрастает, поэтому тангенсу угла наклона прямой к оси х положителен и Δφ /Δx > 0, а Ех < 0, что соответствует рисункам 3 и 4. На участках между заряженными плоскостями и справа от них функция убывает, поэтому на этих участках Δφ /Δx < 0, и Ех > 0, что соответствует рисунку 4.
Ответ: вариант 4.






