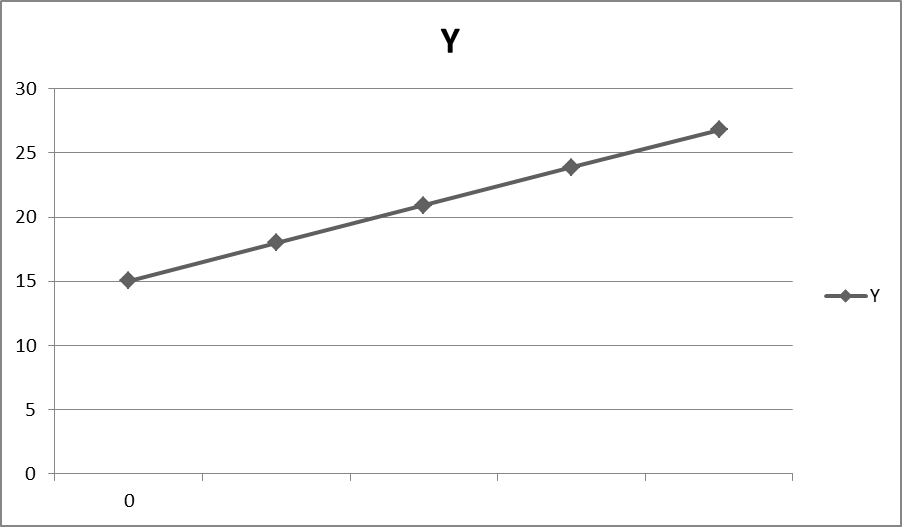
Связь между признаками – среднедушевой доход и среднедушевой оборот розничной торговли.
1. Установить наличие и характер связи между признаками методом аналитической группировки, образовав пять групп с равными интервалами по факторному признаку.
2. Измерить тесноту корреляционной связи между признаками с использованием коэффициента корреляции.
Построим поле корреляции и сделаем вывод о тесноте признаков.
Таблица 12
| Параметры |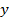 
| 10-15 | 15-20 | 20-25 | 25-30 | 30-35 |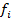 
| |
| 12,5 | 17,5 | 22,5 | 27,5 | 32,5 | |||
| 
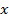
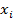
| гр. | ||||||
| 20-26 | **** | |||||||
| 26-32 | * | * | ** | ** | ||||
| 32-38 | **** | ****** | ||||||
| 38-44 | * | *** | * | |||||
| 44-50 | ** | * | ** | |||||
|
|
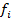
Вывод: Основная масса исследуемой совокупности носит хаотичный порядок.
Определим частоту связи с помощью коэффициента корреляции.
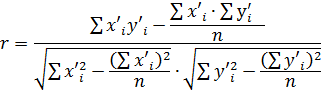
Выполним расчёт коэффициента корреляции:
=23·4·12,5+29·1·12,5+29·1·17,5+29·2·22,5+29·2·27,5+35·4·17,5+35·6·22,5+41·1·17,5+41·3·22,5+41·1·27,5+47·2·22,5+47·1·27,5+47·2·32,5=23170
= 1056 
=12,5·5+17,5·6+22,5·13+27,5·4+32,5·2=635
=92·23+174·29+350·35+205·41+235·47=38826
=62,5·12,5+105*17,5+292,5·22,5+110·27,5+65·32,5=14337,5
Вывод, связь между признаками прямая слабая. Подтвердим данный вывод уравнением регрессии.
Используя метод аналитической группировки, рассчитаем коэффициенты уравнения регрессии нанесем линии регрессии на поле корреляции.
Общий вид уравнения регрессии y= 
+ 
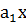
=3,77
=0,49
Рассчитаем значение результативного признака:
= 
17,98
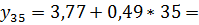20,92
26,8
