«адача 1. ћатематический ма€тник длиной l1=40 см и физический ма€тник в виде тонкого пр€мого стержн€ длиной l2=60 см синхронно колеблютс€ около одной и той же горизонтальной оси. ќпределить рассто€ние a центра масс стержн€ от оси колебаний.
–ешение:
ѕри синхронном колебательном движении ма€тников их периоды равны 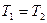 ,
,
где 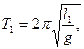
 .
.
ќтсюда
 (1)
(1)
ћомент инерции физического ма€тника определ€етс€ по теореме Ўтейнера:
 (2)
(2)
ѕодставив (2) в (1), получим квадратное уравнение
 (3)
(3)
»з (3) найдем два корн€: a1=10 см, a2=30 см.
“аким образом, при одном и том же периоде колебаний физического ма€тника возможны два варианта расположени€ оси.
¬еличину (1) называют приведенной длиной физического ма€тника.
ќтвет: a1=10 см, a2=30 см.
«адача 2. ¬ вакууме распростран€етс€ плоска€ электромагнитна€ волна. јмплитуда напр€женности магнитного пол€ волны 0,1 ј/м. ќпределить энергию, переносимую этой волной через поверхность площадью 1 м2, расположенную перпендикул€рно направлению распространени€ волны, за врем€ t = 1 с. ѕериод волны T<< t.
–ешение:
ѕлотность потока энергии электромагнитной волны определ€етс€ вектором ѕойнтинга:
 , где
, где  и
и 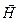 Ц векторы напр€женности электромагнитного и магнитного полей. ”читыва€, что векторы
Ц векторы напр€женности электромагнитного и магнитного полей. ”читыва€, что векторы  и
и 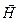 электромагнитной волны взаимно перпендикул€рны, дл€ модул€ вектора p получим
электромагнитной волны взаимно перпендикул€рны, дл€ модул€ вектора p получим
p = EH.
“ак как величины E и H в каждой точке волны мен€ютс€ со временем по гармоническому закону, наход€сь в одинаковых фазах, то мгновенное значение p равно
p = Em 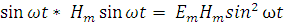
Ёнерги€, переносима€ через площадку S, перпендикул€рную направлению распространени€ волны, в единицу времени,

”читыва€, что в электромагнитной волне
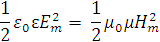
найдем:
Em = Hm 
“огда выражение (*) принимает вид
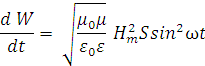
Ёнерги€, переносима€ волной за врем€ t, равна
W = 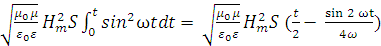
ѕо условию T<< t, поэтому  ; тогда
; тогда
W = 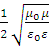
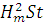
ѕодставл€€ числовые значени€, получим
W = 
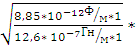 (0,1 ј/м)2
(0,1 ј/м)2  1 м2
1 м2  1 с = 1,88 ƒж
1 с = 1,88 ƒж
ќтвет: W = 1,88 ƒж.
«адача 3. –адиусы кривизны поверхностей линзы R1 = R2 = 20 см. ќпределить: а) фокусное рассто€ние линзы в воздухе; б) фокусное рассто€ние этой же линзы, погруженной в жидкость (nж = 1,7). ѕоказатель преломлени€ материала линзы nл = 1,5.
–ешение:
‘ормула тонкой линзы

ѕрименим данную формулу дл€ случа€ (a), когда линза находитс€ в воздухе, учитыва€, что R1 = R2 = R

отсюда
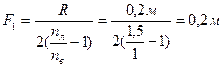
ƒл€ случа€ (б), когда линза погружена в жидкость
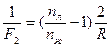
откуда
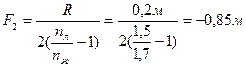
ќтвет: F1 = 0,2 м; F2 = - 0,85 м
«адача 4. ”становка дл€ получени€ колец Ќьютона освещаетс€ монохроматическим светом, падающим по нормали к поверхности пластинки. Ќаблюдение ведетс€ в отраженном свете. –ассто€ние между вторым и двадцатым темными кольцами Δ τ2,20 = 4,8 мм
Ќайти рассто€ние между дев€тым и шестнадцатым темными кольцами Ќьютона.
–ешение:
–адиус темных колец в отраженном свете определ€етс€ формулой:
τR = 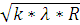 , где
, где
𝑘 Ц пор€дковый номер кольца;
λ Ц длина волны;
R Ц радиус кривизны линзы.
|
|
|
ќтсюда
(1) Δ τ2,20 = 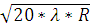 -
-  =
= 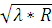 (
( Ц
Ц 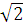 )
)
(2) Δ τ9,16 = 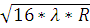 -
-  =
= 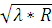 (
( Ц
Ц  ) =
) = 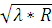
»з (1) имеем
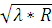 =
= 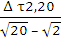 , подставим в (2)
, подставим в (2)
Δ τ9,16 = 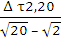 =
= 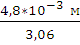 = 1,57
= 1,57 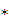 10 Ц 3 м
10 Ц 3 м
ќтвет: Δ τ9,16 = 1,57 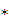 10 Ц 3 м = 1,57 мм
10 Ц 3 м = 1,57 мм
«адача 5. Ќа дифракционную решетку нормально падает монохроматический свет. ќпределить угол дифракции дл€ линии λ1 = 550 нм в четвертом пор€дке, если этот угол дл€ линии λ2 = 600 нм в третьем пор€дке составл€ет 30˚.
–ешение:
‘ормула дифракционной решетки дл€ двух линий
dsinφ1 = 4 λ1 (1)
dsinφ2 = 3 λ2 (2)
ѕоделим уравнение (1) на уравнение (2) и получим
 =
= 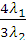 или
или  =
= 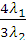
откуда sinφ1 =  =
=  = 0,61
= 0,61
φ1 = arcsin 0,61 = 37˚42΄
ќтвет: φ1 = 37˚42΄
«адача 6. Ќайдите угол полной пол€ризации (iЅр) при отражении света от стекла (nc = 1,57), помещенного в воду (nв = 1,33). ќпределить скорость света в воде.
–ешение:
—огласно закону Ѕрюстера tg iЅр = 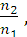 при этом n1 = nв; n2 = nс
при этом n1 = nв; n2 = nс
“огда tg iЅр =  = 1,18, следовательно, iЅр = arctg 1,18 ≈ 50˚
= 1,18, следовательно, iЅр = arctg 1,18 ≈ 50˚
јбсолютный показатель преломлени€ среды n =  , тогда, зна€ nв, найдем скорость распространени€ света в воде: V =
, тогда, зна€ nв, найдем скорость распространени€ света в воде: V = 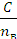 =
=  = 2,26
= 2,26  108
108 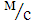
ќтвет: iЅр ≈ 50˚; V = 2,26  108
108 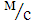
«адача 7. “емпература внутренней поверхности электрической печи
T = 700˚C. ќпределите мощность излучени€ печи через небольшое отверстие диаметром d = 5 см, рассматрива€ его как излучение абсолютно черного тела.
–ешение:
»з закона —тефана Ц Ѕольцмана энергетическа€ светимость (излучательность) черного тела R = σ  T 4. ƒругой стороны, N = R
T 4. ƒругой стороны, N = R  S, где S Ц площадь отверсти€.
S, где S Ц площадь отверсти€.
S = ѕ  τ 2 = ѕ (
τ 2 = ѕ ( ) 2 =
) 2 = 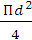 , подставим
, подставим
N = R  S = σ
S = σ  T 4 *
T 4 * 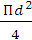 =
= 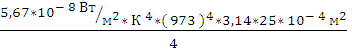 = 9,97
= 9,97  101 = 99,7 ¬т
101 = 99,7 ¬т
ќтвет: N = 99,7 ¬т
«адача 8. расна€ граница фотоэффекта дл€ металла λк = 6,2  10 Ц 5 см. Ќайти величину запирающего напр€жени€ дл€ фотоэлектронов при освещении металла светом длиной волны λ = 330 нм.
10 Ц 5 см. Ќайти величину запирающего напр€жени€ дл€ фотоэлектронов при освещении металла светом длиной волны λ = 330 нм.
–ешение:
«апирающее напр€жение Ц это напр€жение на электродах, способное остановить электроны, вылетевшие из металла. —ледовательно, работа сил электрического пол€ јэ равна кинетической энергии фотоэлектронов. јэ = ≈к или е  U = ≈к. инетическую энергию определ€ем из уравнени€ Ёйнштейна.
U = ≈к. инетическую энергию определ€ем из уравнени€ Ёйнштейна.
hν = Aвых + ≈к => Eк = hν - Aвых
≈сли известна красна€ граница фотоэффекта, то работа выхода определ€етс€ из выражени€ Aвых = h 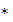 νк = h
νк = h 
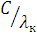
ѕодставим е  U = h
U = h 
 - h
- h 
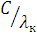 = h
= h  C
C  )
)
откуда U = 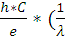 -
- 
U = 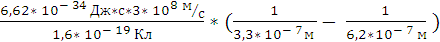 = 1,76 ¬
= 1,76 ¬
ќтвет: U = 1,76 ¬






