Получим аппроксимацию уравнения (1.1) на конечномерных подпространствах 
и 
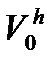, аппроксимирующих исходные пространства 
и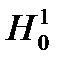 
. Для этого заменим функцию 
аппроксимирующей её функцией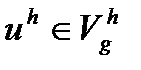 
, а функцию 
функцией 
:
+ 
+ 
= 
+ 
+ 
.
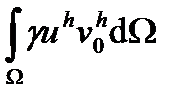Поскольку любая функция может быть представлена в виде линейной комбинации 
, то полученное вариационное уравнение эквивалентно следующей системе уравнений:
+ 
+ 
= 
+ 
+ 
.
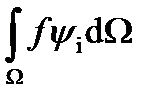Поскольку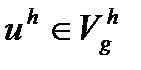 
, оно может быть представлено в виде 
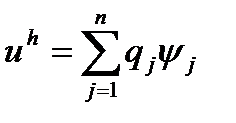в итоге получаем СЛАУ для компонент 
вектора весов q с индексами 
:
= 
+ 
+ 
.
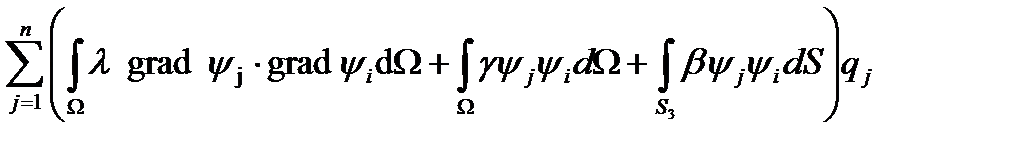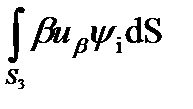При решении исходной краевой задачи с использованием базисных функций, принимающих нулевые значения во всех узлах сетки, кроме одного, конечноэлементная СЛАУ для вектора весов q может быть записана в матричном виде: Aq = b, где компоненты матрицы А и вектора b определяются соотношениями
= 
= 
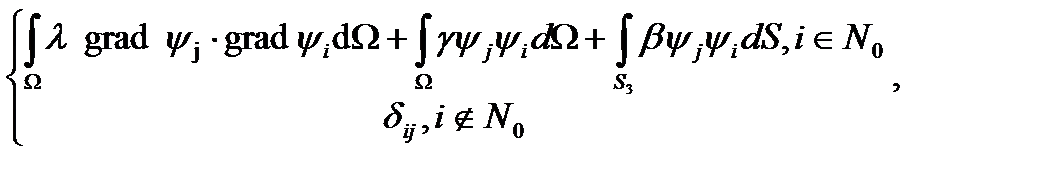
, эти будем интегралы вычислять как сумму интегралов по конечным элементам 
, на которые разбита расчётная область:
= 
= 
, 
,
= 
= 
,
= 
= 
, .
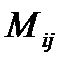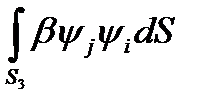В полярных координатах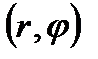 
примут компоненты локальных матриц вид
= 
, 
= 
.
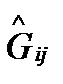Компоненты локального вектора правой части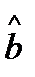 
конечного элемента определяются как 
.
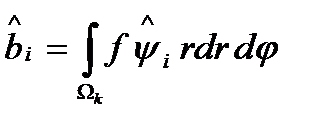Также формулы эти можно записать в виде 
.
Билинейные базисные функции:
На отрезке 
задаются две одномерные линейные функции
= 
, 
= 
, 
= 
.
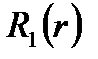Аналогично на интервале 
задаются линейные функции
= 
, 
= 
, 
= 
.
Локальные базисные функции на конечном элементе 
= 
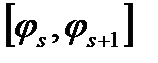представляются в виде произведений:
= , 
= ,
= , 
= .
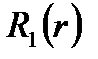
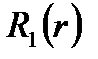
Биквадратичные базисные функции:
= , = , 
= 
,
= 
, 
= 
, 
= 
,
= 
, 
= 
, 
= 
.
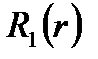
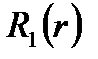
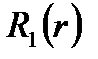
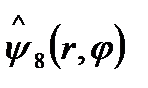