Приклад
Механічна система (рис.*) складається з чотирьох тіл, маси яких відповідно дорівнюють m1, m2, m3, m4. Тіло 2 рухається по похилій шорсткій площині, коефіцієнт тертя ковзання при русі тіла 2f. Блок 3 – східчастий, причому радіусі його ступенів r та R, де 2r=R, радіус інерції і3х . Блок 4 має радіус r.
Скласти диференціальні рівняння руху механічної системи, якщо тіла з’єднані невагомими нерозтяжними нитками.
Розв’язування
Розглядаємо рух механічної системи з чотирьох тіл, з’єднаних між собою нерозтяжними нитками. Застосуємо рівняння Лагранжа ІІ роду у вигляді ().
Розглядувана механічна система має 2 степеня вільності. За узагальнені координати (їх число дорівнює числу степеней вільності) приймемо
Тоді рівняння Лагранжа ІІ роду в наведеній задачі мають вигляд:
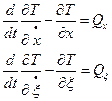(а)
Розглянемо спочатку ліві частини (а). Для цього складемо вираз кінетичної енергії системи в узагальнених швидкостях.
Так тіло 2 в поступальному русі, то його кінетична енергія
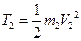або 
, бо 
Тіло 3 в обертальному русі навколо нерухомої осі, його кінетична енергія
, де 
Визначимо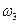 
через швидкість точки К, яка належить тілу 3 і при цьому її швидкість дорівнює 
(так як точка К і тіло 2 з’єднані однією віткою нитки):
, тоді 
, а
.
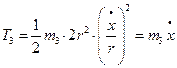Тіло 4 в плоско-паралельному русі, його кінетична енергія
. Тут 
, 
; 
. (б)
Тоді 
Тіло 1 знаходиться у складному поступальному русі. Його кінетична енергія 
. При цьому 
. (в)
Отже, 
Вираз кінетичної енергії системи має вигляд
Проведемо операції, зазначені в лівих частинах рівнянь Лагранжа ІІ роду для розглядуваної задачі (а):
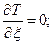
Перейдемо до розгляду правих частин виразів (а), а саме визначимо узагальнені сили як коефіцієнти, що стоять у виразі суми можливих робіт всіх активних сил, що діють на тіла системи, при відповідних варіаціях узагальнених координат.
Активними силами є сили ваги всіх тіл, а також сила тертя ковзання тіла 1.
Так як нитка невагома, абсолютно гнучка і нерозтяжна, а на осі блока тертя відсутнє, то їх вважаємо ідеальними в’язями. Похилу площину також вважаємо ідеальною в’яззю за умови, що дотичну складову її реакції, а саме силу тертя ковзання, віднесемо до активних сил.
Виразимо 
і 
через 
і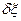 
, через користуючись кінематичними залежностями (б) і (в):
Отже
З останнього виразу отримуємо узагальнені сили
Підставляємо всі отримані при розв’язуванні задачі співвідношення в (а) і знаходимо диференціальні рівняння руху механічної системи:
Висновок: Пропонуємо студентам порівняти отримані результати при розв’язуванні задачі за допомогою загального рівняння динаміки та з використанням рівнянь Лагранжа ІІ роду. Очевидно, що вони збігаються.
