МОДУЛЬ 5
Филонович А.В. кафедра электроснабжения
Тел. 89038734025
1. Линеаризовать уравнение характеристики элемента умножения y=x1x2 в точке y0=x01x02.
y= k1Δx1+k2Δx2, где k1= x02; k2 =x01
2. Найти уравнение Коши состояния САУ, описываемой дифференциальным уравнением 
, где g - входная величина; y - выходная величина.
3. Найти уравнение выхода САУ, описываемой дифференциальным уравнением , где g - входная величина; y - выходная величина.
4.. Определить критический коэффициент усиления Ккр системы, разомкнутая передаточная функция которой 
.
Ккр=2.
5. Определить количество правых корней m системы третьего порядка, годограф Михайлова которой имеет вид
m = 2.
6. Определить порядки астатизма по управляющему g(t) и возмущающему f(t) воздействиям САУ, структурная схема которой приведена на рисунке.
астатизм равен 1.
7. Определить предельное значение коэффициента передачи k нелинейного элемента из условия обеспечения абсолютной устойчивости нелинейной системы, передаточная функция линейной части которой
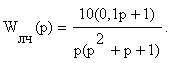
8.. Дать заключение об устойчивости импульсной системы, характеристическое уравнение которой D(z)=10z3+4z2+6z+2+0.
импульсная система устойчива.
9. Оценить свойства управляемости САУ, заданной уравнениями состояния
где: 
САУ полностью управляема
10. Оценить свойства наблюдаемости САУ, заданной уравнениями состояния
где:
САУполностью навблюдаема
11. Определить управляемость САУ третьего порядка n=3 с одним управляющим воздействием m=1, представленных уравнениями состояния x=Ax + Bu с матрицами системы А и В вида
САУ полностью управляема
12. Найти уравнение Коши состояния САУ, описываемой дифференциальным уравнением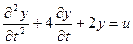 
, где g - входная величина; y - выходная величина.
;
13. Найти уравнение выхода САУ, описываемой дифференциальным уравнением, 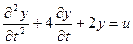где g - входная величина; y - выходная величина.
Y=X1
14. Найти уравнение Коши состояния САУ, описываемой дифференциальным уравнением 
, где u - входная величина; Z - выходная величина
15. Найти уравнение выхода САУ, описываемой дифференциальным уравнением, , где u - входная величина; Z - выходная величина
Z=X1
16. Написать уравнения состояния САУ, имеющей матрицы состояния:
; 
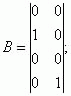C= 
.
В соответствии с матрицами А,В и С уравнения состояния запишем в виде:
17. Характеристическое уравнение замкнутой САУ имеет 3 порядок 1+W(р)=0,
Т1Т2р3+(Т1+Т2)р2+р+К=а0р3+а1р2+а2р+а3=0. Определить устойчивость САУ для следующих параметров: К=80, Т1=0,12с., Т2=0,05с. Условие устойчивости не выполняется, САУ будет устойчивой при К=Ккр=28.
18. Оценить устойчивость САУ третьего порядка с характеристическим уравнением Т1Т2р3+(Т1+Т2)р2+р+К=а0р3+а1р2+а2р+а3=0. Определить устойчивость САУ для следующих параметров: К=80, Т1=0,12с., Т2=0,05с. С использованием частотного критерия Михайлова
Построим годограф Михайлова для V=0 и U=0. Получим, что условие устойчивости не выполняется, САУ будет устойчивой при К=Ккр=28.
19. Для заданных воздействий: скоростное V=20мм/с., постоянное ускорение 
=3мм/с2, гармоническое с амплитудой Хмах=4мм и период Тп=8с. Определить ошибку САУ с передаточной функцией W(р)=К/Р(Т1Р+1)(Т2Р+1), где к=6,6, Т1=0,12с., Т2=0,05с. Чувствительность двигателя Uтр=6В.
Статическая ошибка E0=0.9мм.
Скоростная ошибка Eск=3мм.
20. Оценить устойчивость САУ третьего порядка с характеристическим уравнением Т1Т2р3+(Т1+Т2)р2+р+К=а0р3+а1р2+а2р+а3=0. Определить устойчивость САУ для следующих параметров: Ккр=28, Т1=0,12с., Т2=0,05с. С использованием частотного критерия Найквиста. Построить годограф Найквиста и определить устойчивость САУ.
К(Т1+Т2)<1;
0,476<1 САУ устойчива по критерию Найквиста.
