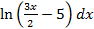I:{{363}} ТЗ-31; t=0; k=4; ek=0; m=0; c=0;
S: Множество первообразных функции 
равно
+: 
-: 
-: 
-: 
I:{{364}} ТЗ-32; t=0; k=4; ek=0; m=0; c=0;
S: Множество первообразных функции 
равно
+: 
-: 
-: 
-: 
I:{{365}} ТЗ-33; t=0; k=4; ek=0; m=0; c=0;
S: Множество первообразных функции 
равно
+: 
-: 
-: 
-: 
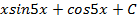
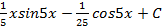
I:{{366}} ТЗ-34; t=0; k=3; ek=0; m=0; c=0;
S: Если в неопределенном интеграле 
, применяя формулу интегрирования по частям: 
, положить, что 
, то функция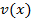 
будет равна
+: 
-: 
-: 
-: 
I:{{367}} ТЗ-35; t=0; k=3; ek=0; m=0; c=0;
S: Если в неопределенном интеграле 
, применяя формулу интегрирования по частям: , положить, что 
, то функция 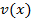будет равна
+: 
-: 
-: 
-: 
I:{{368}} ТЗ-36; t=0; k=3; ek=0; m=0; c=0;
S: Если в неопределенном интеграле 
, применяя формулу интегрирования по частям: , положить, что 
, то функция 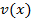будет равна
+: 
-: 
-: 
-: 
I:{{369}} ТЗ-37; t=0; k=3; ek=0; m=0; c=0;
S: Если в неопределенном интеграле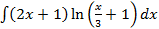 
, применяя формулу интегрирования по частям: , положить, что 
, то функция 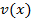будет равна
+: 
-: 
-: 
-: 
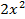
I:{{370}} ТЗ-38; t=0; k=3; ek=0; m=0; c=0;
S: Если в неопределенном интеграле 
, применяя формулу интегрирования по частям: , положить, что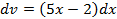 
, то дифференциал функции 
будет равен
+: 
-: 
-: 
-: 
I:{{371}} ТЗ-39; t=0; k=3; ek=0; m=0; c=0;
S: Если в неопределенном интеграле 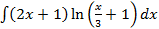, применяя формулу интегрирования по частям: , положить, что 
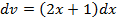, то дифференциал функции будет равен
+: 
-: 
-: 
-: 
I:{{372}} ТЗ-40; t=0; k=3; ek=0; m=0; c=0;
S: Если в неопределенном интеграле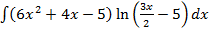 
, применяя формулу интегрирования по частям: , положить, что 
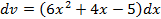, то дифференциал функции будет равен
+: 
-: 
-: 
-: 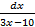