Введем в рассмотрение множество X, состоящего из n элементов, т.е. 
, где символом 
обозначается мощность множества. Элементы множества X будем называть вершинами. Обозначим за X (2) множество всевозможных пар из X и введем в рассмотрение множество Y, являющееся подмножеством X (2). Графом G будем называть пару множеств 
. Пара 
называется неупорядоченной, если 
. Если множество X (2) состоит из неупорядоченных пар, то граф называют неориентированным, а элементы множества Y называют ребрами. Поскольку ребро задается парой вершин, можно говорить, что ребро соединяет одну вершину с другой.
Дадим несколько определений, необходимых для последующего изложения.
· Вершины, которыми задается ребро, называются концевыми вершинами для этого ребра.
· Ребро и вершина являются инцидентными, если вершина концевая для данного ребра.
· Ребро называется петлей, если оно соединяет вершину саму с собой.
· Два или более ребер называются кратными ребрами, если они соединяют одну и ту же пару вершин. При этом степенью кратности будем называть число ребер, соединяющих данную пару вершин.
· Граф называется обыкновенным графом, если он не имеет петель и кратных ребер.
· Ребра называются смежными ребрами, если они имеют общую концевую вершину.
· Вершины называются смежными вершинами, если они соединены ребром.
· Путем в графе из вершины 
в вершину 
называется последовательность из неповторяющихся вершин, каждая из которых смежна со своими соседями. При этом данная последовательность начинается с и заканчивается .
· Пара вершин и называется связными вершинами, если существует путь из одной вершины в другую. В этом случае также говорят, что вершина достижима из .
· Граф называется связным графом, если существует хотя бы по одному пути из одной вершины до всех остальных.
· Разобьем множество вершин на два подмножества 
. Разрезом связного графа G будем называть подмножество ребер 
такое, что при удалении этих ребер, граф G перестает быть связным и распадается на два связных подграфа, первый из которых состоит из вершин, входящих в V, а второй – из вершин, входящих в W. Разрезом для вершин и будем называть такой разрез, при котором 
, а 
.
В настоящей работе ограничимся рассмотрением только обыкновенных неориентированных графов.
Граф, как правило, изображают двумя способами. В виде диаграммы или в виде матрицы смежности, как это показано на рис. 1. Матрица заполняется следующим образом. В ячейке с индексом (i, j) записывается коэффициент кратности для ребер между вершинами i и j. Таким образом, матрица смежности является квадратной матрицей, симметричной относительно главной диагонали. Размер матрицы равен числу вершин (или мощности множества X).
В так называемом случайном графе 
каждому ребру ставится в соответствие вероятность его существования. Таким образом, случайным графом будем называть совокупность трех множеств 
. Первые два множества – это множество вершин и множество ребер. Третье множество – это множество вероятностей существования ребра, причем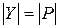 
.
Случайные графы часто используют в прикладных задачах оценки надежности систем. Наиболее наглядным примером является описание с помощью случайных графов сетей связи, как это показано на рис. 2. В этом случае с вершинами ассоциируются вычислительные машины, входящие в сеть, а с ребрами – линии связи, соединяющие машины друг с другом.
Сети связи не единственное применение случайных графов. Любая многоэлементная система может быть представлена подобным образом. На самом деле множество вероятностей P также может быть связано с множеством вершин, определяя существование или отсутствие последних. Однако в данном курсе будут рассматриваться только случайные графы со случайными ребрами.
Оценками надежности случайного графа будут являться вероятность его связности 
или вероятность связности пары вершин в нем 
.
