Рассматриваемые здесь показатели применяются для оценки надежности как невосстанавливаемых (одноразового использования), так и подлежащих ремонту, т.е. восстанавливаемых объектов до появления первого отказа.
Вероятность безотказной работы P(t) вероятность того, что в заданном интервале времени (0, t) в системе или элементе не произойдет отказ.
Статистически Р(t) определяется как отношение числа элементов N(t), безотказно прорабо1ави1их до момента t, к первоначальному числу наблюдаемых элементов N(0):
Р(t) = N(t)/ N(0) (3.1)
Число работоспособных в течение времени (0, t) элементов будет:
N(t)= N(0)-n (0, t) (3.2)
где n(0, t) – число отказавших за время (0, t) элементов.
Очевидно, что
0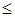 
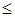Р(t) 1 P(0)=1 P( ∞ )=0
Вероятность появления отказа Q(t) — вероятность того, что в заданном интервале времени (О, t) произойдет отказ.
Статистическая оценка Q(t):
Q(t)= n(О, t)/N(0) (3/3)
Таким образом, всегда имеет место соотношение
Р(t) +Q(t)=1 (3.4.)
Частота отказов а(t) – производная от вероятности появления отказа, означающая вероятность того, что отказ элемента произойдет за единицу времени (t, t+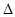 
t).
a(t)= 
(3.5)
Для определения величины a(t) можно использовать статистическую оценку:
a(t)=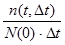 
(3.6)
где n(t, 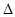t) – число элементов, отказавших в интервале времени от t до 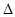t+ t.
Точность статистической оценки (3.6) возрастает с увеличением первоначального числа наблюдаемых элементов и уменьшением временного интервала 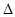t.
Частота отказов, вероятность безотказной работы и вероятность появления отказа связаны следующими зависимостями:
P(t)= 
(3.7)
Q(t)= 
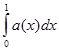(3.8)
Интенсивность отказов 
– условная вероятность отказа после момента t за единицу времени 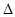t при условии, что до момента tотказа элемента не было.
Интенсивность отказов связана с частотой отказов и вероятностью безотказной работы:
=a(t)/P(t) (3.9)
Так как P(t)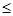 
1, то всегда выполняется соотношение. 
a(t).
Статистически интенсивность отказов определяется таким образом:
a(t)= 
(3.10)
Различие между частотой и интенсивностью отказов в том, что первый показатель характеризует вероятность отказа за интервал (t, t+ 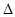t) элемента, взятого из группы элементов произвольным образом, причем неизвестно, в каком состоянии (работоспособном или неработоспособном) находится выбранный элемент. Второй показатель характеризует вероятность отказа за тот же интервал времени элемента, взятого из группы оставшихся работоспособными к моменту t элементов.
Отметим важную особенность, вытекающую из формулы (3.9) для высоконадежных элементов и систем: если P(t)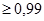 
, то а(t)= 
. Поэтому в практических расчетах возможна при указанном условии взаимная замена а(t) и .
Интегрируя выражение (3.9), получаем формулу для определения вероятности безотказной работы в зависимости от интенсивности отказов и времени:
P(t)=exp[-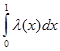 
] (3.11)
Рассмотренные показатели надежности связаны между собой соотношениями, приведенными в сводной таблице 3.1.
Таблица 3.1.
| Известный показатель | Формулы для определения неизвестных показателей | |||
| P(t) | Q(t) | a(t) | .
| |
| P(t) | - | 1-P(t) |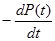 
| 
|
| Q(t) | 1-Q(t) | - |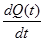 
| 
|
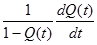
| a(t) |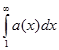 
|
| - | 
|
| .
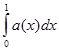
| exp[- ]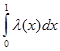
| 1-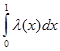exp[- ]
| exp[- ]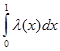
| - |
ИЗМЕНЕНИЕ ИНТЕНСИВНОСТИ ОТКАЗОВ ВО ВРЕМЕНИ
Типичная функция интенсивности отказов во времени (в течение срока службы объекта) имеет U-образный характер (см. рис. 3.1).
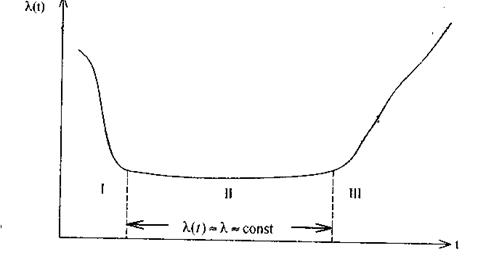
В начальный период I преобладают приработочные отказы. После него наступает наиболее продолжительный период нормальной эксплуатации II, в котором на объект воздействуют случайные факторы. Последние вызывают внезапные отказы, интенсивность которых в период нормальной эксплуатации практически не зависит от времени.
В период старения и износа III в основном имеют место постепенные отказы, возникающие вследствие накопления ухудшений физико-химических свойств объекта.
Для основных элементов СЭС период приработки длится до 3-5 лет. Процессы старения и износа проявляются для ВЛ на опорах из пропитанной древесины через 15-20 лет после ввода в эксплуатацию, для трансформаторов и КЛ через 20-30 лет (в первую очередь за счет старения изоляции). Старение и износ коммутационной аппаратуры наступает через 40-50 лет. Обычно эта аппаратура морально устаревает раньше, нежели физически. В основном элементы СЭС высоконадежны. Время их безотказной работы значительно превышает время восстановления.
Средняя наработка на отказ (среднее время безотказной работы) Т представляет собой математическое ожидание наработки объекта до первого отказа. Этот показатель геометрически представляет собой площадь под кривой вероятности безотказной работы:
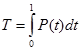(3.12)
РАСЧЕТНЫЕ ФОРМУЛЫ ДЛЯ ЭКСПОНЕНЦИАЛЬНОГО ЗАКОНА НАДЕЖНОСТИ
Учитывая, что для объектов СЭС интенсивность отказов в период нормальной эксплуатации практически неизменна, т.е. 
, приведенные в табл. 3.1 соотношения между основными показателями надежности можно представить с учетом этого условия в более простой и наглядной форме:
P(t)=exp(-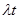 
) (3.13)
Q(t)=1- exp(- 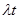) (3.14)
a(t)= 
exp(- 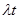) (3.15)
Формулы (3.13)—(3.15) характеризуют экспоненциальный закон надежности, т.е. экспоненциальное распределение времени безотказной работы при отказах с постоянной интенсивностью.
Формула (3.12) для определения средней наработки на отказ для экспоненциального закона принимает вид
T=1/ (3.16)
Для статистической оценки величины Т применяется формула
(3.17)
где t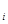 
, – время безотказной работы i-го элемента (объекта)
Если рассматривается один часто выходящий из строя элемент, то в формуле (3.17) под t 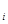, понимается время безотказной работы на i-м интервале времени, а под N(0) – число временных интервалов.
Для экспоненциального закона надежности средняя наработка элемента до первого отказа равна среднему времени безотказной работы между соседними отказами. Поскольку в период нормальной эксплуатации = const, то и Т = const.
На рис. 3.2 представлены в графической форме зависимости основных показателей надежности от времени при экспоненциальном законе. Площадь заштрихованной области численно характеризует среднюю наработку на отказ.
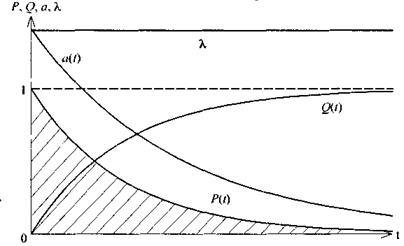
рис.3.2.
Подавляющее большинство объектов СЭС характеризуется очень малыми численными значениями интенсивности отказов и, соответственно, большими значениями средней наработки на отказ. Поэтому экспоненты, получаемые по формулам (3.13-3.15), имеют в реальном масштабе очень пологий вид. Это дает основание заменить их прямыми, касательными к экспонентам в точке t= 0. Математически это означает разложение экспоненты в ряд Тейлора и отбрасывание членов ряда, имеющих высокий порядок малости.
