Общие положения деления средств измерений на классы точности, способы нормирования метрологических характеристик и обозначения классов точности устанавливает ГОСТ 8.401-80.
Класс точности средства измерений - обобщенная характеристика, определяемая пределами допускаемых и дополнительных погрешностей, а также другими свойствами, влияющими на точность, значения которых устанавливаются в стандартах. Класс точности характеризует точность приборов, но не является показателем точности. Пределы допускаемых погрешностей выражают в форме приведенной, относительной или абсолютной погрешностей.
Нормирование погрешности. Существует несколько способов нормирования:
1. Если аддитивная погрешность больше мультипликативной, то удобнее нормировать абсолютную или приведенную погрешность:
,
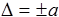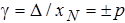, (4.1)
где g - предел допускаемой приведенной основной погрешности, %; D - предел допускаемой абсолютной основной погрешности; xN - нормируемое значение измеряемой величины (обычно верхнее значение шкалы), р - отвлеченное число, выбираемое из ряда предпочтительных чисел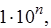 
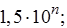
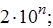
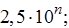
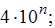
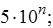
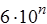(n = 1, 0, -1, -2 и т. д.).
Нормирование по абсолютной величине не позволяет сравнивать приборы с разным диапазоном измерений, поэтому нормируют приведенную погрешность.
Если нормировать относительную погрешность, то получим гиперболу
.
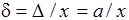Приведенная основная погрешность позволяет сравнивать по точности приборы, имеющие разные пределы измерений, но она не применяется как характеристика погрешности результата измерения.
2. Если мультипликативная погрешность больше аддитивной, то нормируют предел допускаемой относительной погрешности:
d = D/ x = ± q, (4.2)
где q - число, выбираемое из ряда р.
3. Если обе погрешности значительны, то нормируют предел допускаемой относительной погрешности:
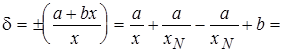
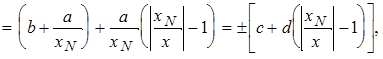(4.3)
c = b + d, d = a/xN.
Анализ формулы:
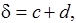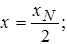
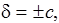если 
если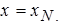 
Таким образом, с - предел допускаемой относительной погрешности при максимальном показании прибора.
Формула вида (9) используется при нормировании приборов высокой точности (цифровых приборов).
Погрешности СИ при нормировании округляют до двух значащих цифр. Дополнительная погрешность выражается так же, как и основная.
Для СИ устанавливаются пределы допускаемых отклонений каждой величины от нормальной. Для СИ за пределами нормального диапазона (но в пределах рабочей области) составляющие погрешности основной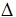 
и дополнительных 
складываются:
.
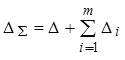