Метрология — наука об измерениях, методах и средствах обеспечения их единства и способах достижения требуемой точности[1].
Единство измерений - состояние измерений, характеризующихся тем, что их результаты выражаются в узаконенных единицах, размеры которых в установленных пределах равны размерам единиц, воспроизводимых первичными эталонами, а погрешности результатов измерений известны и с заданной вероятностью не выходят за установленные пределы[1].
Физическая величина — одно из свойств физического объекта (физической системы, явления или процесса), общее в качественном отношении для многих физических объектов, но в количественном отношении индивидуальное для каждого из них[1].
Истинное значение физической величины — значение физической величины, которое идеальным образом характеризует в качественном и количественном отношении соответствующую физическую величину[1].
Истинный размер физической величины- объективная реальность, которая не зависит от того, измеряют ее или нет и которая идеальным образом характеризует свойства объекта.
Так как истинное значение мы не знаем, то вместо него используют понятие действительного значения.
Действительное значение физической величины - значение физической величины, полученное экспериментальным путём и настолько близкое к истинному значению, что в поставленной измерительной задаче может быть использовано вместо него[1].
Шкала физической величины — упорядоченная совокупность значений физической величины, служащая исходной основой для измерений данной величины[1].
Измерение — совокупность операций по применению технического средства, хранящего единицу физической величины, обеспечивающих нахождение соотношения (в явном или неявном виде) измеряемой величины с её единицей и получение значения этой величины[1].
Измерение- это процесс сравнения искомой величины с величиной, размер которой равен 1.
Q=n*[Q]- уравнение измерений,
Q- Измеряемая физическая величина,
[Q]- качественная характеристика ФВ,
n- Количественная характеристика, которая показывает, во сколько раз измеряемая величина отличается от той величины, размер которой принят за единицу.
[Q]- ее размер принимаем за единицу. Напр., размер детали 20 мм, мы сравниваем р-р с 1 мм.
Измерительная задача — задача, заключающаяся в определении значения физической величины путём её измерения с требуемой точностью в данных условиях измерений[1].
По способу получения информации измерения делятся:
1. Прямые измерения - измерения, при которых искомое значение физической величины находят непосредственно из опытных данных, и их можно выразить Q= x, где Q- искомое значение измеряемой величины, а x- значение, получаемое из опытных данных. Например, измерение длины тела с использованием ШЦ, линейки и т.д. измерение осуществляется с помощью СИ, шкалы которых проградуированы в единицах измеряемой величины.
Прямые измерения лежат в основе всех последующих измерений.
2. Косвенные измерения (косвенный метод измерений) — определение искомого значения физической величины на основании результатов прямых измерений других физических величин, функционально связанных с искомой величиной[1]. Например, объем детали Q=V=S*h.
3. Совокупные измерения — проводимые одновременно измерения нескольких одноимённых величин, при которых искомые значения величин определяют путём решения системы уравнений, получаемых при измерениях этих величин в различных сочетаниях (число уравнений должно быть не менее числа величин)[1]. Например, определение массы тела при помощи разновесов; определение сопротивления, индуктивности при последовательных и параллельных соединениях.
4. Совместные измерения — проводимые одновременно измерения двух или нескольких неодноимённых величин для определения зависимости между ними[1]. Неодноименные величины различаются по своей природе. Например, необходимо определить зависимость сопротивления от температуры, давления
Характеристики измерений:
Принцип измерений — физическое явление или эффект, положенное в основу измерений.
Метод измерений — приём или совокупность приёмов сравнения измеряемой физической величины с её единицей в соответствии с реализованным принципом измерений[1].
Основные методы измерений:
· Метод непосредственной оценки — метод измерений, при котором значение величины определяют непосредственно по показывающему средству измерений[1].
· Метод сравнения с мерой — метод измерений, в котором измеряемую величину сравнивают с величиной, воспроизводимой мерой[1]. Методы сравнения с мерой:
o а) Нулевой метод измерений — метод сравнения с мерой, в котором результирующий эффект воздействия измеряемой величины и меры на прибор сравнения доводят до нуля[1].
o б) Метод измерения замещением — метод сравнения с мерой, в котором измеряемую величину замещают мерой с известным значением величины[1].
o в) Метод измерений дополнением — метод сравнения с мерой, в котором значение измеряемой величины дополняется мерой этой же величины с таким расчётом, чтобы на прибор сравнения воздействовала их сумма, равная заранее заданному значению[1].
o г) Дифференциальный метод измерений — метод измерений, при котором измеряемая величина сравнивается с однородной величиной, имеющей известное значение, незначительно отличающееся от значения измеряемой величины, и при котором измеряется разность между этими величинами[1].
Погрешность измерения — отклонение результата измерения от истинного (действительного) значения измеряемой величины (истинное значение величины неизвестно, его применяют только в теоретических исследованиях. На практике используют действительное значение величины)[1]
Точность измерений — одна из характеристик качества измерения, отражающая близость к нулю погрешности результата измерения[1].

Сходимость результатов измерений — близость друг к другу результатов измерений одной и той же величины, выполненных повторно одними и теми же средствами, одним и тем же методом в одинаковых условиях и с одинаковой тщательностью[1].
Воспроизводимость результатов измерений — близость результатов измерений одной и той же величины, полученных в разных местах, разными методами, разными средствами, разными операторами, в разное время, но приведённых к одним и тем же условиям измерений (температуре, влажности и т.д.) (воспроизводимость может характеризоваться средними квадратическими погрешностями сравниваемых рядов измерений)[1].
Средство измерений — техническое средство, предназначенное для измерений, имеющее нормированные метрологические характеристики, воспроизводящее и (или) хранящее единицу физической величины, размер которой принимают неизменным (в пределах установленной погрешности) в течение известного интервала времени[1].
Вид средств измерений — совокупность средств измерений, предназначенных для измерений величин определённого вида (средства измерения массы, линейный величин...)[2].
Классификация средств измерений:
1. Мера — средство измерений, предназначенное для воспроизведения и (или) хранения физической величины одного или нескольких заданных размеров, значения которых выражены в установленных единицах и известны с необходимой точностью (однозначная, многозначная меры, набор мер, магазин мер)[1].
o Однозначная мера — мера, воспроизводящая физическую величину одного размера.
o Набор мер — комплект мер разного размера одной и той же физической величины, предназначенных для применения на практике, как в отдельности, так и в различных сочетаниях (набор КМД)[1].
o Магазин мер — набор мер, конструктивно объединённых в единое устройство, в котором имеются приспособления для их соединения в различных комбинациях (например, магазин электрических сопротивлений)[1].
Номинальное значение меры — значение величины, приписанное мере или партии мер при изготовлении. Действительное значение меры — значение величины, приписанное мере на основании её калибровки или поверки[1].
2. Измерительный прибор — средство измерений, предназначенное для получения значений измеряемой физической величины в установленном диапазоне[1].
3. Измерительная установка — совокупность функционально объединённых мер, измерительных приборов, измерительных преобразователей и других устройств, предназначенная для измерений одной или нескольких физических величин и расположенная в одном месте[1].
4. Измерительная система — совокупность средств измерений, образующих измерительные каналы, вычислительных и вспомогательных устройств, функционирующая как единое целое и предназначенная для автоматического (автоматизированного) получения информации о состоянии объекта путём измерительных преобразований в общем случае, множества изменяющихся во времени и распределённых в пространстве величин, характеризующих это состояние; машинной обработки результатов измерений; регистрации и индикации результатов измерений и результатов машинной обработки; преобразования этих данных в выходные сигналы системы. Измерительные системы удовлетворяют признакам средств измерений и относятся к средствам измерений[2].
5. Измерительный преобразователь.
6. Измерительная машина.
7. Измерительные принадлежности — вспомогательные средства, служащие для обеспечения необходимых условий для выполнения измерений с требуемой точностью (не являются средством измерения)[1].
Метрологические характеристики средств измерений — характеристики свойств средства измерений, оказывающих влияние на результаты и погрешности измерений, предназначенные для оценки технического уровня и качества средства измерений, для определения результатов измерений и расчётной оценки характеристик инструментальной составляющей погрешности измерений[2].
Шкала — часть показывающего устройства средства измерений, представляющая собой упорядоченный ряд отметок вместе со связанной с ним нумерацией[1].
Деление шкалы — промежуток между двумя соседними отметками шкалы средства измерений[1].
Цена деления шкалы — разность значений величины, соответствующих двум соседним отметкам шкалы средства измерений[1].
Начальное значение шкалы — наименьшее значение измеряемой величины, которое может быть отсчитано по шкале средства измерений[1].
Конечное значение шкалы — наибольшее значение измеряемой величины, которое может быть отсчитано по шкале средства измерений.
Вариация показаний измерительного прибора — разность показаний прибора в одной и той же точке диапазона измерений при плавном подходе к этой точке со стороны меньших и больших значений измеряемой величины[1].
Диапазон показаний — область значения шкалы прибора, ограниченная начальным и конечным значениями шкалы[1].
Диапазон измерений — область значений величины, в пределах которой нормированы допускаемые пределы погрешности средства измерений[1].
Динамическая характеристика средства измерений — МХ свойств средства измерений, проявляющихся в том, что на выходной сигнал этого средства измерений влияют значения входного сигнала и любые изменения этих значений во времени[2].
Стабильность средства измерений — качественная характеристика средства измерений, отражающая неизменность во времени его МХ[1].
Погрешности средств измерений и измерений:
Абсолютно точно измерить ничего нельзя. Результат измерения зависит от множества факторов:- применяемого метода измерения,
- применяемого СИ,
-условий проведения измерений,
-от способа обработки результатов измерения,
-квалификации операторов ит.д.
Эти факторы по-разному сказываются на отличии результата измерения от истинного значения величины. Прежде всего: 1) существует погрешность от замены истинного значения действительным. 2) погрешность используемого метода измерения, причем каждый из методов вносит определенный вклад в погрешность. 3) Т.к. любая зависимость между измеряемой величиной и др. величинами выводится на основании некоторых допущений, то при использовании этой зависимости допускается теоретическая (методическая) погрешность. 4) Само средство измерения является источником погрешности, т.к. его несовершенство, искажение характерных признаков измеряемой величины(входного сигнала), поступающих на вход СИ в процессе выполняемых измерит. преобразований.
Погрешность средства измерений — разность между показанием средства измерений и истинным (действительным) значением измеряемой физической величины.
Погрешность измерения — отклонение результата измерения от истинного (действительного) значения измеряемой величины (истинное значение величины неизвестно, его применяют только в теоретических исследованиях. На практике используют действительное значение величины)[1]

Погрешность средства измерений в интервале влияющей величины — погрешность средства измерений в условиях, когда одна из влияющих величин принимает любые значения в пределах рабочей области её значений, а остальные влияющие величины находятся в пределах, соответствующих нормальным условиям (ГОСТ 8.050-73 «Нормальные условия выполнения линейных и угловых измерений»). Примечание: Погрешность средства измерений в интервале влияющей величины не является дополнительной погрешностью, поскольку последняя обусловлена только отличием значения влияющей величины от нормального значения[2].
Систематическая погрешность — составляющая погрешности результата измерения, остающаяся постоянной или закономерно изменяющаяся при повторных измерениях одной и той же физической величины[1].
Инструментальная погрешность - составляющая погрешности измерения, обусловленная погрешностью применяемого средства измерений[1].
Погрешность метода — составляющая систематической погрешности измерений, обусловленная несовершенством принятого метода измерений[1].
Субъективная погрешность — составляющая систематической погрешности измерений, обусловленная индивидуальными особенностями оператора[1].
Случайная погрешность — составляющая погрешности результата измерения, изменяющаяся случайным образом (по знаку и значению) при повторных измерениях, проведённых с одинаковой тщательностью, одной и той же физической величины[1].
Абсолютная погрешность — погрешность измерения, выраженная в единицах измеряемой величины[1].

Относительная погрешность — погрешность измерения, выраженная отношением абсолютной погрешности измерения к действительному или измеренному значению измеряемой величины[1].

Систематическая составляющая погрешности средства измерений — составляющая погрешности данного экземпляра средства измерений, при одном и том же значении измеряемой или воспроизводимой величины и неизменных условиях применения средства измерений остающаяся постоянной или изменяющаяся настолько медленно, что её изменениями за время проведения измерения можно пренебречь, или изменяющаяся по определённому закону, если условия изменяются[2].
Случайная составляющая погрешности средства измерений — случайная составляющая погрешности средства измерений, обусловленная только свойствами самого средства измерений; представляет собой центрированную случайную величину или центрированный случайный процесс[2].
Погрешность результата однократного измерения — погрешность одного измерения (не входящего в ряд измерений), оцениваемая на основании известных погрешностей средства и метода измерений в данных условиях[1].
Суммарная погрешность — погрешность результата измерений (состоящая из суммы случайных и неисключённых систематических погрешностей, принимаемых за случайные), вычисляемая по формуле[1].

Класс точности средств измерений — обобщённая характеристика данного типа средств измерений, как правило, отражающая уровень их точности, выражаемая пределами допускаемой основной и дополнительных погрешностей, а также другими характеристиками, влияющими на точность[1].
Классы точности средств измерений [3]
Пределы допускаемой основной погрешности устанавливаются в последовательности, приведённой ниже.
Пределы допускаемой абсолютной основной погрешности устанавливают по формуле:
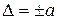 (1)
(1)
или,  (2)
(2)
где Δ — пределы допускаемой абсолютной основной погрешности, выраженной в единицах измеряемой величины на входе (выходе) или условно в делениях шкалы;
x — значение измеряемой величины на входе (выходе) средств измерений или число делений, отсчитанных по шкале;
a, b — положительные числа, не зависящие от x.
В обоснованных случаях пределы допускаемой абсолютной погрешности устанавливают по более сложной формуле или в виде графика либо таблицы.
Пределы допускаемой приведённой основной погрешности следует устанавливать по формуле
 , (3)
, (3)
где γ — пределы допускаемой приведённой основной погрешности, %
Δ - пределы допускаемой абсолютной основной погрешности,устанавливаемые по формуле (1);
XN – нормирующее значение, выраженное в тех же единицах, что и Δ;
p — отвлечённое положительное число, выбираемое из ряда 1∙10n; 1,5∙10n;(1,6∙10n);2∙10n;2,5∙10n;(3∙10n);4∙10n;5∙10n;6∙10n (n=1, 0, -1, -2 и т. д.) (*)
Значения, указанные в скобках, не устанавливают для вновь разрабатываемых средств измерений.
Нормирующее значение XN для средств измерений с равномерной, практически равномерной или степенной шкалой, а также для измерительных преобразователей, если нулевое значение входного (выходного) сигнала находится на краю или вне диапазона измерений, следует устанавливать равным большему из пределов измерений или равным большему из модулей пределов измерений, если нулевое значение находится внутри диапазона измерений.
Для электроизмерительных приборов с равномерной, практически равномерной или степенной шкалой и нулевой отметкой внутри диапазона измерений нормирующее значение допускается устанавливать равным сумме модулей пределов измерений.
Для средств измерений физической величины, для которых принята шкала с условным нулём, нормирующее значение устанавливают равным модулю разности пределов измерений.
Для средств измерений с установленным номинальным значением значением нормирующее значение устанавливают равным этому номинальному значению.
Пределы допускаемой относительной основной погрешности устанавливают по формуле:
 , (4)
, (4)
если Δ установлено по формуле (1) или по формуле
 , (5)
, (5)
где δ — пределы допускаемой относительной основной погрешности, %
q – отвлечённое положительное число,
Xk – больший (по модулю) из пределов измерения,
c и d — положительные числа, выбираемые из ряда (*).
В обоснованных случаях пределы допускаемой относительной основной погрешности устанавливают по более сложной формуле или в виде графика, либо таблицы.
Классам точности, которым соответствуют меньшие пределы допускаемых погрешностей, должны соответствовать буквы, находящиеся ближе к началу алфавита, или цифры, означающие меньшие числа.
В эксплуатационной документации на средство измерений конкретного вида, содержащей обозначение класса точности, должна быть ссылка на стандарт или технические условия, в которых установлен класс точности этого средства измерений.
Правила построения и примеры обозначения классов точности в документации и на средствах измерений приведены в таблице.
Практически равномерная шкала — шкала, длина делений которой отличается друг от друга не более, чем на 30% и имеет постоянную цену делений [3].
| Форма выражения погрешности | Пределы допускаемой основной погрешности | Пределы допускаемой основной погрешности, % | Обозначение класса точности | |
| в документации | на средстве измерений | |||
| Приведённая по | По формуле (3): если нормирующее значение выражено в единицах величины на входе(выходе) средств измерений если нормирующее значение принято равным длине шкалы или её части |


| Класс точности 1,5 Класс точности 0,5 |
1,5
  0,5 0,5
|
| Относительная по | По формуле (4) По формуле (5) |  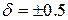

| Класс точности 0,5 Класс точности 0,02/0,01 |  0,02/0,01
0,02/0,01
|
| Абсолютная по | По формуле (1) или (2) | Класс точности М Класс точности С | М С |
Нормальные условия выполнения линейных и угловых измерений [4]
В зависимости от условий проведения измерений погрешности делятся на: основные и дополнительные.
Основная погрешность – погрешность, соответствующая нормальным условиям, которые устанавливаются нормативными документами на виды СИ.
Нормальные условия должны обеспечиваться при измерениях для практического исключения дополнительных погрешностей.
Нормальные значения основных влияющих величин:
1. Температура окружающей среды 20 оС по ГОСТ 9249-59.
2. Атмосферное давление 101325 Па (760 мм рт. ст.).
3. Относительная влажность окружающего воздуха 58% (нормальное парциальное давление водяных паров 1333 Па).
4. Ускорение свободного падения (ускорение силы тяжести) 9,8 м/с2.
5. Направление линии и плоскости измерения линейных размеров — горизонтальное (90о от направления силы тяжести).
6. Положение плоскости измерения углов — горизонтальное (90о от направления силы тяжести).
7. Относительная скорость движения внешней среды равна нулю.
8. Значения внешних сил, кроме силы тяжести, атмосферного давления, действия магнитного поля Земли и сил сцепления элементов измерительной системы (установки) равны нулю.
Результаты измерения для сопоставимости должны приводиться к нормальным значениям влияющих величин с погрешностью, не превышающей 35% допускаемой погрешности измерения.
Обработка результатов измерений с многократными независимыми наблюдениями:
Требуется изучить совокупность однородных объектов относительно некоторого качественного или количественного признака, характеризующего объект (качественный признак — стандартность детали, количественный — контролируемый параметр детали). Иногда проводится сплошное обследование, т. е. обследуется каждый из объектов совокупности. На практике осуществить это сложно, т. к. совокупность содержит очень большое количество объектов. Поэтому в таких случаях из совокупности случайным образом отбирается ограниченное число объектов (выборка), подвергаемая изучению. На основании полученных результатов делается вывод обо всей совокупности.
Выборочная совокупность (выборка) — совокупность случайно отобранных объектов.
Генеральная совокупность — вся совокупность объектов, из которых производится выборка.
Результат измерения - значение величины, полученное путём её измерения[1].
Ряд результатов — значения одной и той же величины, последовательно полученные из следующих друг за другом измерений.
Рассеяние результатов в ряду измерений — несовпадение результатов измерений одной и той же величины в ряду равноточных измерений, как правило, обусловленное действием случайных погрешностей. Оценками рассеяния результатов в ряду измерений могут быть: размах, средняя арифметическая погрешность (по модулю), средняя квадратическая погрешность (по модулю), средняя квадратическая погрешность или стандартное отклонение (среднее квадратическое отклонение, экспериментальное среднее квадратическое отклонение)[1].
Размах результатов измерений — оценка Rn рассеяния результатов единичных измерений физической величины, образующих ряд (или выборку из n измерений), вычисляемая по формуле
 ,
,
где Xmax и Xmin — наибольшее и наименьшее значения физической величины в данном ряду измерений (рассеяние обычно обусловлено проявлением случайных причин при измерении и носит вероятностных характер)[1].
Результаты наблюдений в значительной степени сконцентрированы вокруг истинного значения измеряемой величины, и по мере приближения к нему элементы вероятности их появления возрастают. При многократных измерениях информация об истинном значении измеряемой величины и рассеивании результатов наблюдений состоит из ряда результатов отдельных наблюдений Х1, Х2, …Хn, где n – число наблюдений. Их можно рассматривать как n независимых случайных величин. В этом случае в качестве оценки измеряемой величины можно принять среднее арифметическое полученных результатов наблюдений.
 .
.
Среднее арифметическое представляет собой лишь оценку математического ожидания (МО) результата измерения и может стать оценкой истинного значения измеряемой величины только после исключения систематических погрешностей.
Особое значение наряду с МО результатов измерений дает дисперсия – характеристика рассеивания результатов относительно МО. Дисперсия не всегда удобна в использовании, поэтому используют среднее квадратическое отклонение результатов наблюдений.
Средняя квадратическая погрешность результатов единичных измерений в ряду измерений (средняя квадратическая погрешность, СКП) — оценка S рассеяния единичных результатов измерений в ряду равноточных измерений одной и той же физической величины около среднего их значения, вычисляемого по формуле
 ,
,
где Xi – результат i-го единичного измерения,
- среднее арифметическое значение измеряемой величины из n единичных результатов.
При обработке ряда результатов измерений, свободных от систематических погрешностей, СКП и СКО являются одинаковой оценкой рассеяния результатов измерений[1].
Средняя квадратическая погрешность результата измерений среднего арифметического — показывает отклонение выборочного среднего от математического ожидания.
 ,
,
где S – средняя квадратическая погрешность результатов единичных измерений, полученная из ряда равноточных измерений; n — число единичных измерений в ряду[1].
Доверительные границы погрешности результата измерений — наибольшее и наименьшее значения погрешности измерений, ограничивающие интервал, внутри которого с заданной вероятностью находится искомое (истинное) значение погрешности результата измерений. (Доверительные границы в случае нормального закона распределения вычисляются как ±tр·S, где tр – коэффициент, зависящий от доверительной вероятности P и числа измерений n)[1].
Границы доверительного интервала определяются как:
( )
)
Поправка — значение величины, вводимое в неисправленный результат измерения с целью исключения составляющих систематической погрешности (знак поправки противоположен знаку погрешности)[1].
Критерий отсеивания промахов для наперёд заданной доверительной вероятности (критерий Романовского) — для всех результатов Xi, не являющихся выбросами (промахами) выполняются следующие условия:
 ,
,
где tp — квантиль (коэффициент).
Промах — погрешность результата отдельного измерения, входящего в ряд измерений, которая для данных условий резко отличается от остальных результатов этого ряда (промах — грубая погрешность измерений)[1].
Предельная погрешность измерения в ряду измерений — максимальная погрешность измерения (плюс, минус), допускаемая для данной измерительной задачи ()[1].
Нормальное распределение случайных величин возникает тогда, когда на результат измерения действует множество факторов (случайных), ни один из которых не является преобладающим.
Функция нормального распределения:
 ,
,
где Xi – i-е значение случайной величины (СВ),
M[X] – математическое ожидание СВ,
σx – СКО отдельного результата измерений.
Нормальный закон распределения.






