Статические модели принципиально отличаются от динамических прежде всего тем, что в них не учитывается время появления ошибок в процессе тестирования и не используется никаких предположений о поведении функции риска. Эти модели строятся на твердом статическом фундаменте.
3.2.1. Модель Миллса
Использование этой модели предполагает необходимость перед началом тестирования искусственно вносить в программу (засорять) некоторое количество известных ошибок. Ошибки вносятся случайным образом и фиксируются в протоколе искусственных ошибок. Специалист, проводящий тестирование, не знает ни количества ошибок, ни характера внесенных ошибок до момента оценки показателей надежности по модели Миллса. Предполагается, что все ошибки (как естественные, так и искусственно внесенные) имеют равную вероятность быть найденными в процессе тестирования.
Тестируя программу в течение некоторого времени, собирается статистика об ошибках. В момент оценки надежности по протоколу искусственных ошибок все ошибки делятся на собственные и искусственные. Соотношение:
(3.15)
дает возможность оценить N – первоначальное количество ошибок в программе. В данном соотношении, которое называется формулой Миллса, S – количество искусственно внесенных ошибок, n – число найденных собственных ошибок, V – число обнаруженных к моменту оценки искусственных ошибок.
Вторая часть модели связанна с проверкой гипотезы от N. Предположим, что в программе имеется К собственных ошибок, и внесем в нее еще S ошибок. В процессе тестирования были обнаружены все S внесенных ошибок и n собственных ошибок.
Тогда по формуле Миллса мы предполагаем, что первоначально в программе было N = n ошибок. Вероятность, с которой можно высказать такое предположение, возможно рассчитать по следующему соотношению:
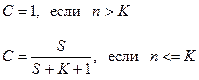(3.16)
Таким образом, величина С является мерой доверия к модели и показывает вероятность того, насколько правильно найдено значение N. Эти два связанных между собой по смыслу соотношения образуют полезную модель ошибок: первое предсказывает возможное первоначально имевшихся в программе ошибок, а второе используется для установления доверительного уровня прогноза. Однако формула (5.2) для расчета C не может быть в случае, когда не обнаружены все искусственно рассеяние ошибки. Для этого случая, когда оценка надежности производиться до момента обнаружения всех S рассеянных ошибок, величина C рассчитывается по модифицируемой формуле
(3.17)
где числитель и знаменатель формулы при n <= K являются биноминальными коэффициентами вида
(3.18)
Например, если утверждается, что в программе нет ошибок, а к моменту оценки надежности обнаруженно 5 из 10 рассеянных ошибок и не обнаружено ни одной собственной ошибки, то вероятность того, что в программе действительно нет ошибок, будет равна:
(3.19)
Если при тех же исходных условиях оценка надежности производится в момент, когда обнаруженны 8 из 10 искусственных ошибок, то вероятность того, что в программе не было ошибок, увеличивается до 0.73. В действительности модель Миллса можно использовать для оценки N после каждой найденной ошибки. Предлагается во время всего периода тестирования отмечать на графике число найденных ошибок и текущее значение для N. Достоинством модели является простота применения математического аппарата, наглядность и возможность использования в процессе тестирования.
Однако она не лишена и ряда недостатков, самые существенные из которых – это необходимость внесения искусственных ошибок (этот процесс плохо формализуется) и достаточно вольное допущения величины K, которое основывается исключительно на интуиции и опыте человека, проводящего оценку, т.е. допускается большое влияние субъективного фактора.
3.2.2. Модель Липова
Липов модифицировал модель Миллса, рассмотрев вероятность обнаружения ошибки при использовании различного числа тестов. Если сделать то же предположение, что и модель Миллса, т.е. что собственные и искусственные ошибки имеют равную вероятность быть найденными, то вероятность обнаружения n собственных и V внесенных ошибок равна:
(3.20)
где m – количество тестов, используемых при тестировании;
q - вероятность обнаружения ошибки в каждом из m тестов, рассчитывается по формуле:
(3.21)
S – общее количество искусственно внесенных ошибок;
N – количество собственных ошибок, имеюшихся в ПС до начала тестирования.
Для использования модели Липова должны выполняться следующие условия:
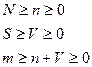(3.22)
Модель Липова дополняет модель Миллса, дав возможность оценить вероятность обнаружения определенного количества ошибок к моменту оценки.
