Задание 3

Структурная схема надежности приведена на рис 3.1. Значения интенсивности отказов элементов даны в 1/ч

Рис. 3.1. Исходная схема системы

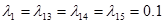
1. В исходной схеме элементы 2, 3 и 4 образуют параллельное соединение. Заменяем их квазиэлементом A. Учитывая, что , получим

(3.1)

2. Элементы 5 и 6 образуют параллельное соединение. Заменяем их квазиэлементом B. Учитывая, что , получим

(3.2)

3. Элементы 8 и 9 в исходной схеме соединены так же параллельно. Заменяем их элементом С, для которого при

(3.3)

4. В исходной схеме элементы 10, 11 и 12 образуют параллельное соединение. Заменяем их квазиэлементом D. Учитывая, что , получим

(3.4)

5. Элементы 13, 14 и 15 образуют соединение “2 из 3”, которое заменяем элементом E. Так как , то для определения вероятности безотказной работы элемента F можно воспользоваться комбинаторным:

(3.5)

6. Преобразованная схема изображена на рис. 3.2.

Рис. 3.2. Преобразованная схема

Элементы A, B, C, D и 7 образуют (рис. 3.2) мостиковую систему, которую можно заменить квазиэлементом F.

7. Для расчета вероятности безотказной работы воспользуемся методом разложения относительно особого элемента, в качестве которого выберем элемент 7. Тогда

(3.6)

где - вероятность безотказной работы мостиковой схемы при абсолютно надежном элементе 7 (рис. 3.3, а), - вероятность безотказной работы мостиковой схемы при отказавшем элементе 7 (рис. 3.3, б).

а б

Рис. 3.3. Преобразования мостиковой схемы при аболютно надежном (а) и абсолютно ненадежном (б) элементе 7.

Получаем формулу для элемента F:

(3.7)

8. В преобразованной схеме (рис. 3.4) элементы 1, F и E образуют последовательное соединение. Тогда вероятность безотказной работы всей системы

(3.8)

Рис. 3.4. Преобразованная схема

9. Так как по условию все элементы системы работают в периоде нормальной эксплуатации, то вероятность безотказной работы элементов с 1 по 14 (рис. 3.1) подчиняются экспоненциальному закону:

(3.9)

10. Результаты расчетов вероятностей безотказной работы элементов 1 - 14 исходной схемы по формуле (3.9) для наработки до 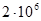часов представлены в таблице 3.1.

11. Результаты расчетов вероятностей безотказной работы квазиэлементов A, B, C, D, E и F по формулам (3.1) - (3.7) также представлены в таблице 3.1.

12. На рис. 3.5 представлен график зависимости вероятности безотказной работы системы P от времени (наработки) t.

13. По графику (рис. 3.5, кривая P) находим для - процентную наработку системы ч.

14. Проверочный расчет при ч показывает (таблица 3.1), что .

15. По условиям задания повышенная - процентная наработка системы ч.

Рис. 3.5. Изменение вероятности безотказной работы исходной системы (Р), системы с повышенной надежностью (Р`) и системы со структурным резервированием элементов (Р``).

16. Расчет показывает (таблица 3.1), что при 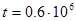ч для элементов преобразованной схемы (рис. 3.4) , и .

Следовательно, из трех последовательно соединенных элементов минимальное значение вероятности безотказной работы имеет элемент F (мостиковая система в исходной схеме (рис. 3.1)) и именно увеличение его надежности даст максимальное увеличение надежности системы в целом. При этом самыми ненадежными элементами являются элемента 2-6 и 8-12.

17. Для того, чтобы при ч система в целом имела вероятность безотказной работы , необходимо, чтобы элемент F имел вероятность безотказной работы (см. формулу (3.8))

(3.10)

Очевидно, значение , полученное по формуле (3.10), является минимальным для выполнения условия увеличения наработки не менее, чем в 1.5раза, при более высоких значениях увеличение надежности системы будет большим.

18. Для определения минимально необходимой вероятности безотказной работы элементов 2-6 и 8-12 (рис. 3.1) необходимо решить уравнение (3.7) относительно при . Однако, т.к. аналитическое выражение этого уравнения связано с определенными трудностями, более целесообразно использовать графо-аналитический метод. Для этого по данным табл. 3.1 строим график зависимости . График представлен на рис. 3.6.

Рис. 3.6. Зависимость вероятности безотказной работы мостиковой системы F от вероятности безотказной работы ее элементов.

19. По графику при находим .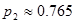

20. Так как по условиям задания все элементы работают в периоде нормальной эксплуатации и подчиняются экспоненциальному закону (3.9), то для элементов 2-6 и 8-12 при 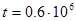находим

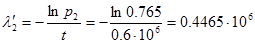ч . (3.11)

21. Таким образом, для увеличения - процентной наработки системы необходимо увеличить надежность элементов 2-6 и 8-12 и снизить интенсивность их отказов с до ч , т.е. в 2.24 раза.

22. Результаты расчетов для системы с увеличенной надежностью элементов приведены в таблице 3.1. Там же приведены расчетные значения вероятности безотказной работы системы F` и системы в целом P`. При 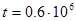ч вероятность безотказной работы системы , что соответствует условиям задания. График приведен на рис 3.5

23. Для второго способа увеличения вероятности безотказной работы системы - структурного резервирования также выбираем элемент F, вероятность безотказной работы которого после резервирования должна быть не ниже (см. формулу (3.10)).

24. Для элемента F – мостиковой системы – резервирование означает дублирование элементов, работоспособность которых влияет на надежность системы в целом. Для резервирования возьмем элемент 7, как самый ненадежный в укрупненной схеме (рис. 3.2, табл. 3.1)

Аналитически определить минимально необходимое количество элементов невозможно, т.к. число элементов должно быть целым и функция 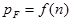дискретна.

25. Для повышения надежности мостиковой системы F добавляем к ней параллельно элемент 7*, идентичный по надежности исходному элементу 7.

При добавлении первого же элемента получаем:

(3.12)

Таким образом простое добавление параллельно элемента 7*, к самому ненадежному элементу 7 дало результат, превышающий ожидаемый.

26. Таким образом, для повышения надежности до требуемого уровня необходимо в схеме (рис. 3.2) мостиковую систему достроить элементом 7* (рис. 3.7).

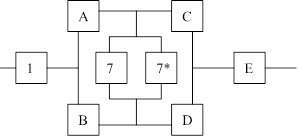
Рис. 3.7. Структурная схема системы после структурного резервирования.

27. Результаты расчетов вероятностей безотказной работы системы F`` и системы в целом P`` представлены в таблице 3.1.

28. Расчеты показывают, что при 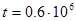ч , что соответствует условию задания.

29. На рис. 3.5 нанесены кривые зависимостей вероятности безотказной работы системы после повышения надежности элементов 2-6 и 8-12 (кривая ) и после структурного резервирования (кривая ).

Выводы

1. На рис. 3.5 представлена зависимость вероятности безотказной работы системы (кривая 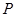). Из графика видно, что 90% - наработка исходной системы составляет часов.

2. Для повышения надежности и увеличения 90% - наработки системы в 1.5 раза (до часов) предложены два способа:

а) повышение надежности элементов 2-6 и 8-12 и уменьшение их отказов с до ч , т.е. в 2.24 раза;

б) нагруженное резервирование элемента 7 идентичным по надежности резервныи элементом 7* (рис. 3.7).

3. Анализ зависимостей вероятности безотказной работы системы от времени (наработки) (рис. 3.5) показывает, что второй способ повышения надежности системы (структурное резервирование) предпочтительнее первого, так как в период наработки до часов вероятность безотказной работы системы при структурном резервировании (кривая ) выше, чем при увеличении надежности элементов (кривая ).

Литература

1. Липаев В.В. Надежность программных средств. Серия «Информатизация России на пороге XXI века». – М.: СИНТЕГ, 1998, 232 с.

2. Закорюкин В.Б. Надежность устройств автоматики. Учебное пособие. МИРЭА – М., 2000, 111 с.

1. Левин В.И. Логическая теория надежности сложных систем. - М.: Энергоатомиздат, 1985. - 128 с.

2. Надежность технических систем: Справочник/Под ред. Ушакова И.А. - М.: Радио и связь, 1985. - 608 с.

3. Нечипоренко В.И. Структурный анализ систем (эффективность и надёжность). - М.: Сов. радио, 1977. - 214 с.

4. Рябинин И.А., Черкесов Г.Н. Логико-вероятностные методы исследования надежности структурно-сложных систем. - М.: Радио и связь, 1981. - 216 с.

5. ГОСТ 27.002 - 83 Надежность в технике. Термины и определения.

6. Сотсков Б. С. Основы теории и расчета надежности элементов и устройств автоматики и вычислительной техники. - М.: Высш. школа, 1970. - 270 с.

Приложение А. Таблица 3.1. Расчет вероятности безотказной работы системы

Элемент	l _i,x10^-6ч^-1	Наработка t, x 106 ч
0,25	0,50	0,75	1,00	1,25	1,50	1,75	2,00	0,40	0,60
	0,1	0,9753	0,9512	0,9277	0,9048	0,8825	0,8607	0,8395	0,8187	0,9608	0,9418
2-6		0,7788	0,6065	0,4724	0,3679	0,2865	0,2231	0,1738	0,1353	0,6703	0,5488
	0,5	0,8825	0,7788	0,6873	0,6065	0,5353	0,4724	0,4169	0,3679	0,8187	0,7408
8-12		0,7788	0,6065	0,4724	0,3679	0,2865	0,2231	0,1738	0,1353	0,6703	0,5488
13-15	0,1	0,9753	0,9512	0,9277	0,9048	0,8825	0,8607	0,8395	0,8187	0,9608	0,9418
A	-	0,9892	0,9391	0,8531	0,7474	0,6368	0,5311	0,4360	0,3535	0,9642	0,9082
B	-	0,9511	0,8452	0,7216	0,6004	0,4909	0,3965	0,3174	0,2524	0,8913	0,7964
C	-	0,9511	0,8452	0,7216	0,6004	0,4909	0,3965	0,3174	0,2524	0,8913	0,7964
D	-	0,9892	0,9391	0,8531	0,7474	0,6368	0,5311	0,4360	0,3535	0,9642	0,9082
E	-	0,9982	0,9931	0,9851	0,9746	0,9618	0,9472	0,9310	0,9133	0,9955	0,9902
F	-	0,9856	0,9035	0,7507	0,5695	0,4010	0,2663	0,1688	0,1032	0,9462	0,8490
P	-	0,9595	0,8535	0,6861	0,5022	0,3404	0,2171	0,1319	0,0772	0,9051	0,7917
2'-6',8'-12'	0,4465	0,8944	0,7999	0,7154	0,6399	0,5723	0,5119	0,4578	0,4095	0,8365	0,7650
A'	-	0,9988	0,9920	0,9770	0,9533	0,9218	0,8837	0,8406	0,7940	0,9956	0,9870
B'	-	0,9888	0,9600	0,9190	0,8703	0,8171	0,7617	0,7060	0,6513	0,9733	0,9448
C'	-	0,9888	0,9600	0,9190	0,8703	0,8171	0,7617	0,7060	0,6513	0,9733	0,9448
D'	-	0,9988	0,9920	0,9770	0,9533	0,9218	0,8837	0,8406	0,7940	0,9956	0,9870
F'	-	0,9971	0,9789	0,9368	0,8701	0,7837	0,6856	0,5841	0,4860	0,9887	0,9651
P'	-	0,9707	0,9247	0,8562	0,7672	0,6652	0,5590	0,4565	0,3634	0,9457	0,9000
7''	-	0,9862	0,9511	0,9022	0,8452	0,7840	0,7216	0,6600	0,6004	0,9671	0,9328
F''	-	0,9996	0,9948	0,9777	0,9415	0,8843	0,8083	0,7193	0,6241	0,9978	0,9899
P''	-	0,9732	0,9398	0,8935	0,8303	0,7506	0,6590	0,5622	0,4667	0,9543	0,9231