Напряжением называется интенсивность внутренней силы, т.е. часть внутренней силы, переходящиеся на единицу площади сечения. Если напряжение распределены равномерно по всей площади, то 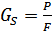 .
.
На практике напряжения распределяются неравномерно и для этого берут небольшую площадку ∆ F, в пределах которой напряжения можно считать равномерными.
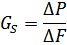
Наиболее точный результат получают:
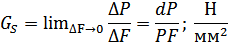
При объяснении процессов обработки давлением удобном пользоваться не усилиями, а напряжениями
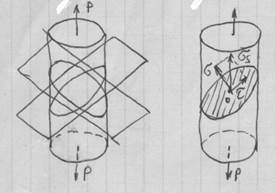
Для произвольно выбранной площадки, под которым углом GS напряжения, можно разложить на нормальную G и касательную τ. Нормальные напряжения, возникающие от действия внешних растягивающих сил (напряжения, растяжения), считаются положительными, а напряжения от сжимающих сил (напряжения, сжатия) – отрицательные.
Из этого следует 2 важных положения.
1. Если известны напряжения какой-либо трех взаимно перпендикулярных плоскостях, проходящих через точку, то можно определить напряжения и в любой четвертой плоскости, проходящей через эту точку. Следовательно, напряженное состояние точнее определенно, если известны напряжения и в трех взаимно перпендикулярных проходящих через нее плоскостях.
2. При любом напряженном состоянии всегда существует 3 и только 3 такие взаимно перпендикулярные плоскости, проходящие через одну точку на которых касательные напряжения равны 0. Нормальные напряжения, которые действуют на этих плоскостях называются главными напряжениями. Направления в которых действуют главные напряжения, называется главными направлениями, а площадки, на которых действуют главные напряжения – главными площадками.






