ќпределение точечных оценок закона распределени€ результатов измерений.Ќа этом этапе определ€ютс€:
Х среднее арифметическое значение х измер€емой величины;
Х — ќ результата измерени€ Sx;
Х — ќ среднего арифметического значени€ Sx̅. √рубые погрешности и промахи исключаютс€, после чего проводитс€ повторный расчет оценок среднего арифметического значени€ и его — ќ. ¬ р€де случаев дл€ более надежной идентификации закона распределени€ результатов измерений могут определ€тьс€ другие точечные оценки: коэффициент асимметрии, эксцесс и контрэксцесс, энтропийный коэффициент.
ќпределение закона распределени€ результатов измерений или случайных погрешностей измерений.¬ последнем случае от выборки результатов измерений х1, х2, х3,-.., хn переход€т к выборке отклонений от среднего арифметического Dх1, Dх2, Dх3,..., Dхn, где Dxi = xi - х̅.
ѕервым шагом при идентификации закона распределени€ €вл€етс€ построение по исправленным результатам измерений xi, где I = 1, 2,..., n, вариационного р€да(упор€доченной выборки), а также уi, где уi = min(xi) и уn = mах(хi). ¬ вариационном р€ду результаты измерений (или их отклонени€ от среднего арифметического) располагают в пор€дке возрастани€. ƒалее этот р€д разбиваетс€ на оптимальное число m, как правило, одинаковых интервалов группировани€длиной h = (y1 + yn) / m.
ќптимальным €вл€етс€ такое число интервалов m, при котором возможное максимальное сглаживание случайных флуктуации данных сопровождаетс€ с минимальным искажением от сглаживани€ самой кривой искомого распределени€. ƒл€ практического применени€ целесообразно использовать предложенные mmin = 0,55n0,4 и mmax =1,25n0,4, которые получены дл€ наиболее часто встречающихс€ на практике распределений с эксцессом, наход€щимс€ в пределах от 1,8 до 6, т.е. от равномерного до распределени€ Ћапласа.
»скомое значение m должно находитс€ в пределах от mmjn до mmax, быть нечетным, так как при четном m в островершинном или двухмодальном симметричном распределении в центре гистограммы оказываютс€ два равных по высоте столбца и середина кривой распределени€ искусственно уплощаетс€. ¬ случае, если гистограмма распределени€ €вно двухмодальна€, число столбцов может быть увеличено в 1,5-2 раза, чтобы на каждый из двух максимумов приходилось примерно по m интервалов. ѕолученное значение длины интервала группировани€ h всегда округл€ют в большую сторону, иначе последн€€ точка окажетс€ за пределами крайнего интервала.
ƒалее определ€ют интервалы группировани€ экспериментальных данных в виде D1 = (у1, y1 + h); D2= (y1 +h, y1 + 2h);....; Dm = (yn - h; уn), и подсчитывают число попаданий nk (частоты)результатов измерений в каждый интервал группировани€. —умма этих чисел должна равн€тьс€ числу измерений. ѕо полученным значени€м рассчитывают веро€тности попадани€ результатов измерений (частости)в каждый из интервалов группировани€ по формуле pk= nk/n, где k=l, 2,..., m.
ѕроведенные расчеты позвол€ют построить гистограмму, полигон и кумул€тивную кривую. ƒл€ построени€ гистограммыпо оси результатов откладываютс€ интервалы Dk в пор€дке возрастани€ номеров и на каждом интервале строитс€ пр€моугольник высотой pk. ¬ этом случае площадь под гистограммой равна единице. ѕри увеличении числа интервалов и соответственно уменьшении их длины гистограмма все более приближаетс€ к гладкой кривой Ч графику плотности распределени€ веро€тности.
|
|
|
ѕолигонпредставл€ет собой ломаную кривую, соедин€ющую середины верхних оснований каждого столбца гистограммы.
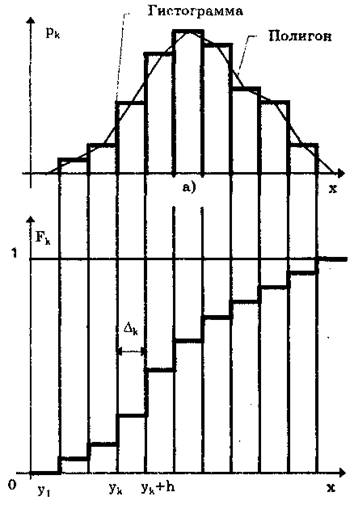
–исунок 1-√истограмма, полигон (а) и кумул€тивна€ крива€ (б)
Ёти точки при построении полигона соедин€ют между собой отрезками пр€мых линий. ¬ результате совместно с осью х образуетс€ замкнута€ фигура, площадь которой в соответствии с правилом нормировани€ должна быть равна единице (или числу наблюдений при использовании частостей).
умул€тивна€ крива€Ч это график статистической функции распределени€. ƒл€ ее построени€ по оси результатов наблюдений х (рисунок 1,6) откладывают интервалы Dk в пор€дке возрастани€ номеров и
на каждом интервале стро€т пр€моугольник высотой p
ѕо виду построенных зависимостей может быть оценен закон распределени€ результатов измерений.
ќценка закона распределени€ по статистическим критери€м. ѕри числе наблюдений n > 50 дл€ идентификации закона распределени€ используетс€ критерий ѕирсона (хи-квадрат) или критерий ћизесаЧ—мирнова (w2). ѕри 50 > n > 15 дл€ проверки нормальности закона распределени€ примен€етс€ составной критерий (d-критерий), приведенный в √ќ—“ 8.207-76. ѕри n < 15 принадлежность экспериментального распределени€ к нормальному не провер€етс€.
ќпределение доверительных границ случайной погрешности.≈сли удалось идентифицировать закон распределени€ результатов измерений, то с его использованием наход€т квантильный множитель zp при заданном значении доверительной веро€тности –. ¬ этом случае доверительные границы случайной погрешности ј = ±zpS.
ќпределение границ неисключенной систематической погрешности q результата измерений.ѕод этими границами понимают найденные нестатистическими методами границы интервала, внутри которого находитс€ неисключенна€ систематическа€ погрешность. ќна образуетс€ из р€да составл€ющих: как правило, погрешностей метода и средств измерений, а также субъективной погрешности. √раницы неисключенной систематической погрешности принимаютс€ равными пределам допускаемых основных и дополнительных погрешностей средств измерений, если их случайные составл€ющие пренебрежимо малы. ƒоверительна€ веро€тность при определении границ 6 принимаетс€ равной доверительной веро€тности, используемой при нахождении границ случайной погрешности.
ќпределение доверительных границ погрешности результата измерени€ Dр. ƒанна€ операци€ осуществл€етс€ путем суммировани€ — ќ случайной составл€ющей Sx̅ и границ неисключенной систематической составл€ющей q в зависимости от соотношени€ q/ Sx̅. –езультат измерени€ записываетс€ в виде х = х̅ ± Dp при доверительной веро€тности – = –. ѕри отсутствии данных о виде функции распределени€ составл€ющих погрешности результаты измерений представл€ют в виде х, S-. п.8 при доверительной веро€тности – = –д.
«аключение
ћногократные измерени€ провод€т с целью уменьшени€ вли€ни€ случайных составл€ющих погрешностей измерени€.
ѕрименение р€дов предпочтительных чисел представл€ет собой параметрическую стандартизацию, котора€ позвол€ет получить значительный эффект на всех стади€х жизненного цикла изделий (проектирование, изготовление, эксплуатаци€ и др.) —тандартами параметров охватываетс€ большой диапазон характеристик изделий: материалы, заготовки, размерный режущий инструмент, оснастка, контрольные калибры, узлы по присоединительным размерам, выходные параметры электродвигателей и многое другое, что используетс€ в той или иной отрасли промышленности.
|
|
|






