Примеры решения задач. Приведем интеграл к табличному с помощью подведения под знак дифференциала выражения

Поиск:

Примеры решения задач. Приведем интеграл к табличному с помощью подведения под знак дифференциала выражения

1.Вычислить .

Решение

Приведем интеграл к табличному с помощью подведения под знак дифференциала выражения . Учитывая, что , получим:

Ответ: .

2.Вычислить .

Решение

На первый взгляд неясно, к какому табличному интегралу приводится этот интеграл. Поэтому наша задача – обнаружить под знаком интеграла некую функцию вместе со своей производной(со своим дифференциалом). Найдем дифференциал от выражения :

Мы замечаем, что под знаком интеграла есть похожее выражение , правда без множителя 4. Умножим и разделим наш интеграл на 4. Получим:

Заменим выражение , стоящее в числителе, равным ему выражением :

( введя мысленно замену , мы привели интеграл к табличному )

Ответ: .

3.Вычислить .

Решение

Поступим аналогичным образом: найдем дифференциал подкоренного выражения :

Домножим и разделим подынтегральную функцию на 6, чтобы выделить под знаком интеграла выражение :

=[используем равенство ]=

Ответ: .

4.Вычислить .

Решение

Заметим, что производная функции равна , а значит, . Заменим в интеграле выражение равным ему выражением . Получим:

Ответ: .

5.Вычислить .

Решение

Напомним, что надо искать под знаком интеграла функцию вместе со своей производной. Заметим, что , а значит, . Заменим в интеграле выражение равным ему выражением . Получим:

Ответ: .

6.Вычислить

Решение

Разобьем интеграл на сумму двух интегралов, разделив почленно числитель на знаменатель:

. (*)

Вычислим теперь каждый из полученных интегралов.

Для вычисления интеграла воспользуемся подведением под знак дифференциала. Заметим, что . Умножим и разделим подынтегральное выражение на –4. Получим:

Вычислим теперь второй интеграл . Вынесем за знак интеграла постоянный множитель для того, чтобы мы могли воспользоваться табличным интегралом XII: . Получим:

Подставим оба вычисленных интеграла в формулу (*) и получим окончательный ответ:

Ответ: .

7.Вычислить

Решение

Разобьем интеграл на сумму двух интегралов, разделив почленно числитель на знаменатель и вычислим каждый из получившихся интегралов.

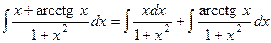Вычислим интеграл . Заметим, что . Следовательно,

(см. пример 7).

Для вычисления интеграла также воспользуемся методом подведения под знак дифференциала, но теперь под знак дифференциала будем заносить функцию , т.к. . Имеем:

Тогда исходный интеграл есть сумма полученных интегралов:

Ответ: .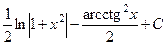

<== предыдущая лекция	\|	следующая лекция ==>
Приложение 3. Приемы вычисления некоторых видов интегралов	\|	Массивы. Задачи комбинированной обработки массивов

Дата добавления: 2015-01-25; просмотров: 463 | Нарушение авторских прав | Изречения для студентов