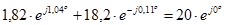 (2.29)
(2.29)
ƒл€ суммировани€ в левой части этого выражени€ необходимо произвести преобразование чисел из показательной в нормальную форму:
 (2.30)
(2.30)
 (2.31)
(2.31)
дл€ правого контура цепи должно выполн€ть соотношение:
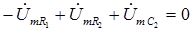 (2.32)
(2.32)
»ли в числовом виде
 (2.33)
(2.33)
ƒл€ суммировани€ в левой части этого выражени€ необходимо произвести преобразование чисел из показательной в нормальную форму:
 (2.34)
(2.34)
 ¬ (2.35)
¬ (2.35)
4. ѕостроение полной векторной диаграммы цепи
ѕостроение векторной диаграммы цепи производитс€ на основе числовых данных, представленных в таблице. ƒл€ каждого тока (напр€жени€) в таблице имеютс€ значени€ модул€ и аргумента. Ќапример, модуль напр€жени€ на сопротивлении Re равен 1,82 ¬, а аргумент равен 1,040. —ледовательно, вектор, соответствующий, будет иметь длину 1,8 см (при масштабе: в 1см 1¬) и угол относительно горизонтальной оси округл€ем до 00.
јналогичным образом стро€тс€ векторы, соответствующие остальным токам и напр€жени€м, приведенным в таблице. ѕри этом все построени€ начинаютс€ из одной точки и угол откладываетс€ в одном направлении. ѕосле построени€ всех векторов, соответствующих токам и напр€жени€м на элементах цепи, проводим вектор, соответствующий комплексной амплитуде источника э.д.с., воздействующего на цепь.
ƒл€ того, чтобы рисунок не был сильно загроможденным построени€ проведены раздельно на разных плоскост€х дл€ напр€жений и токов, как это сделано на рис. 3 и рис. 4 применительно к рассматриваемой схеме (рис. 2).
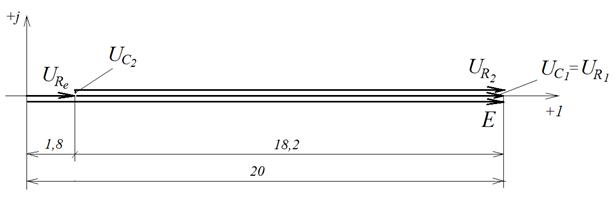
–ис. 3. ¬екторна€ диаграмма напр€жений
ѕоскольку значени€ токов, протекающих через  и
и  в 100раз меньше, чем токи через
в 100раз меньше, чем токи через  и
и  ,то округл€ем меньшее значение тока до 0, т.е.
,то округл€ем меньшее значение тока до 0, т.е. 
¬ыбираем масштаб: в 1см 2мј. “огда, например, вектор, соответствующий  , будет иметь длину 9,1см, угол относительно горизонтальной оси округл€ем до 00.
, будет иметь длину 9,1см, угол относительно горизонтальной оси округл€ем до 00.

–ис. 4. ¬екторна€ диаграмма токов
5. –асчет частотных характеристик цепи
ƒл€ нахождени€ частотных характеристик цепи возможно применение как аналитического расчета, так и использование специализированных программ моделировани€ электрических цепей, например, Electronic Work Bench. –ассмотрим первый вариант.
ѕри проведении аналитического расчета частотных характеристик возможно два варианта:
1) вывод формулы дл€ расчета частотных характеристик в общем виде, а затем подстановка в них значений частот.ѕри этом необходимо получить в общем виде выражение, соответствующее выходному напр€жению цепи, т.е. зависимость  . ƒл€ этого повтор€ютс€ все расчеты (2.1) Ц (2.22) не подставл€€ в формулы числовое выражение частоты ω. ¬ результате этого поучитс€ выражение, содержащее зависимость от частоты;
. ƒл€ этого повтор€ютс€ все расчеты (2.1) Ц (2.22) не подставл€€ в формулы числовое выражение частоты ω. ¬ результате этого поучитс€ выражение, содержащее зависимость от частоты;
2) расчет частотных характеристик по нескольким точкам. ¬ качестве одной из них можно использовать точку с частотой, равной заданной по варианту, а значение второй частоты можно выбрать произвольно и дл€ нее повторить все вычислени€ с самого начала.
ќстановимс€ на последнем варианте как на более простом. –ассмотрим в начале две крайние точки: при частоте, равной нулю, и при частоте, стрем€щейс€ к бесконечности.
|
|
|
¬ первом случае как следует из формулы реактивного сопротивлени€ емкости, реактивные сопротивлени€ —1 и —2 будут стремитьс€ к бесконечности, а следовательно, ток на выходе схемы (через —2), будет равен нулю. Ёто означает, что коэффициент передачи цепи в этом случае равен нулю.
¬о втором случае (при частоте, стрем€щейс€ к бесконечности) сопротивление емкости —1 будет стремитьс€ к нулю. ѕри этом исходна€ схема (рис.2) преобразуетс€ к виду, представленному на рис. 5.

–ис. 5. »сходна€ схема при частоте э.д.с., стрем€щейс€ к бесконечности






