Контрольная работа
по дисциплине
«Надежность, эргономика и качество АСОИУ»
Выполнил: студент группы АСУ-01-з
Пименова Д.Н.
Проверил: Липатов И.Н.
Пермь 2006
Определение количественных характеристик надежности
по статистическим данным об отказах изделия.
Задача 1.9 В течение 1000 час из 10 гироскопов отказало 2. За интервал времени 1000 - 1100 час. отказал еще один гироскоп. Требуется определить f*(t), l*(t) при t =1000 час.
Решeниe.
f*(t) - статистическая оценка частоты отказов изделия
где Dn(t) - число отказавших изделий на участке времени (t, t+Dt);
Dt - интервал врeмени.
l*(t)- статистическая оценка интенсивности отказов изделия
где n(t)- число изделий, не отказавших к моменту времени t; Dn(t) - число отказавших изделий на участке времени (t, t+Dt).
Аналитическое определение количественных характеристик надёжности изделия.
Задача 2.8 Время работы изделия подчинено нормальному закону с параметрами mt = 8000 час., st =1000 час. Требуется вычислить количественные характеристики надежности p(t), f(t), l(t), mt для t=8000 час.
Решeниe.
Воспользуемся формулами
,
,
,
,
для p(t), f(t), l(t),mt.
1. Вычислим вероятность безотказной работы
p(t)=0.5-Ф(U); U=(t-mt)/st;
U=(8000-8000)/1000=0; Ф(0)=0;
p(8000)=0.5-0=0.5.
2. Определим частоту отказа f(t)
.
Введем обозначение
.
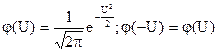Тогда
f(t)=j(U)/st; U=(t-mt)/st 
;
f(8000)=j(0)/1000=0,3989/1000=39.89*10-5 1/час.
3. Рассчитаем интенсивность отказов l(t)
l(t)=f(t)/p(t);
l(8000)=f(8000)/p(8000)=39.89·10-5 /0.5=79.78·10-5 1/час.
4. Среднее время безотказной работы элемента mt =1/l=8000 час.
Последовательное соединение элементов в систему.
Задача 3.10 Система управления состоит из 6000 элементов, средняя интенсивность отказов которых lср. = 0,16*10-6 1/час. Необходимо определить вероятность безотказной работы в течении t = 50 час и среднее время безотказной работы.
Решeниe.
Интенсивность отказов системы по формуле 
будет
lс=lср*n=0,16*10-6*6000=0,96*10-3 1/час.
Тогда на основании формулы
Рc(t)= е-lct
имеем
Рc(50)= е-0,96*0,001*50 = е-0,048»0,953.
определим среднее время безотказной работы mtc:
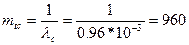часов.
Расчет надежности системы с постоянным резервированием.
Задача 4.6 В радиопередатчике, состоящем из трех равнонадежных каскадов (n=3) применено общее постоянное дублирование всего радиопередатчика. Интенсивность отказов каскада равна l=5*10-4 1/час. Определить Pc(t), mtc, fc(t), lc(t) радиопередатчика с дублированием.
Решeниe.
В данном случае n=3; li=l; l0=nl=3l;m=1.
По формуле Pc(t)=1-(1-e-l0t)m+1 имеем
Рс(t)=1-(1-e-3lt)m+1;
.
Определим mtс. Из формулы 
имеем
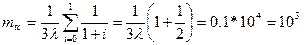час.
Определим частоту отказов fc(t). Получим
Определим интенсивность отказов lс(t). Имеем:
Резервирование замещением в режиме облегченного (теплого) резерва и в режиме ненагруженного (холодного) резерва.
Задача 5.6 Схема расчета надежности системы приведена на рис. 5, где А,Б,В,Г – блоки системы. Определить вероятность безотказной работы Pc(t) системы.
А Б В Г
Рис. 5
Решeниe.
Вероятность безотказной работы системы равна:
блок А – без резервирования (n=2);
блок Б – резервирование замещением в режиме ненагружаемого резерва;
блок В - без резервирования (n=1);
блок Г – режим постоянного резервирования (m=2).
Для блока А вероятность безотказной работы равна:
,
где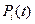 
- вероятности безотказной работы i -го элемента блока А.
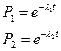
Тогда 
.
Для блока Б вероятность безотказной работы равна:
.
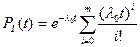Из условия задачи:
,
m = 1.
Тогда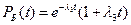 
.
Для блока В вероятность безотказной работы равна:
,
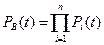где 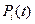- вероятности безотказной работы i -го элемента блока В.
.
Тогда 
.
Для блока Г вероятность безотказной работы равна:
,
где Pj - вероятности безотказной работы элемента резервного элемента j
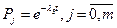
m =2.
Тогда 
Найдем вероятности безотказной работы системы:
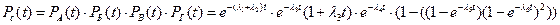
Ответ: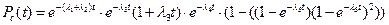 
Расчет надежности системы с поэлементным резервированием.
Задача 6.7 В телевизионном канале связи, состоящем из приемника и передатчика, применено раздельное дублирование передатчика и приемника. Передатчик и приемник имеют интенсивности отказов lп=2*10-3 1/час и lпр=1*10-3 1/час соответственно. Схема канала представлена на рис. 6. Требуется определить вероятность безотказной работы канала Pc(t), среднее время безотказной работы mtc, частоту отказов fc(t), интенсивность отказов lс(t).
 |
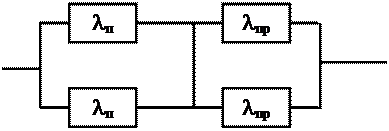Рис. 6
Решeниe.
Вероятность безотказной работы системы равна:
,
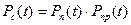где Pп(t), Pпр(t) - вероятности безотказной работы передатчика и приемника (с резервированием).
Для передатчика вероятность безотказной работы равна:
,
где P1 - вероятности безотказной работы резервного элемента передатчика.
Для приемника вероятность безотказной работы равна:
,
где P2 - вероятности безотказной работы резервного элемента передатчика.
Найдем вероятность безотказной работы системы:
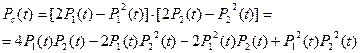
Из условия задачи:
Тогда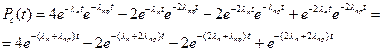 
Подставим исходные данные:
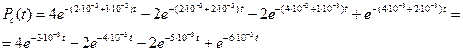
Найдем частоту отказов.
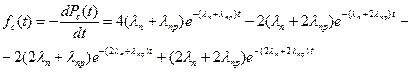
Подставим исходные данные:
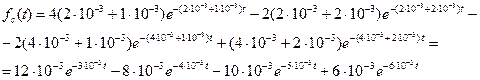
Найдем интенсивность отказов:
Подставим исходные данные:
Найдем среднее время безотказной работы:
Подставим исходные данные:
Ответ:
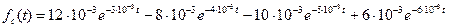
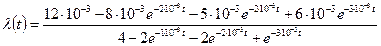
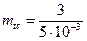
Резервирование с дробной кратностью и постоянно включенным резервом.
Задача 7.5 Автомобильный двигатель имеет l=4 свечи зажигания по одной на каждый цилиндр. Интенсивность отказов свечи l=10-3 1/час, а длительность работы двигателя в течение всего путешествия t=20 час. Предполагается, что автомобиль может ехать также при одном неработающем цилиндре. Необходимо определить вероятность безотказной работы двигателя Pc(t), среднее время безотказной работы двигателя mtc, частоту отказов fc(t), интенсивность отказов lc(t) двигателя. Какова вероятность того, что автомобиль доставит туристов в пункт назначения без замены свечей?
Решeниe.
Найдем вероятность безотказной работы устройства Pc (t):
,
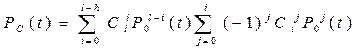где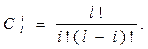 
Ро(t) - вероятность безотказной работы основной системы или любой резервной системы; l - общее число основных и резервных систем; h - число систем, необходимых для нормальной работы.
Из условия задачи:
l = 4
h = 3
Тогда
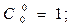
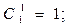
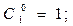
Будем предполагать, что для любой отдельно взятой системы справедлив экспоненциальный закон надежности, т.е.
Тогда
Для данных нашей задачи 
t =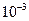 
*20=0,02.
Тогда
Pc(20)=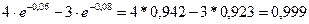 
.
Среднее время безотказной работы на основании формулы (7.4) будет:
час.
Определим частоту отказов fc(t). Имеем
(20)= 
(1/час)
Определим интенсивность отказов lс(t). Получим
.
Скользящее резервирование при экспоненциальном законе надежности.
Задача 8.5 Бортовая аппаратура спутника включает в себя аппаратуру связи, командную и телеметрическую системы, систему питания и систему ориентации. Аппаратура связи состоит из двух работающих ретрансляторов и одного ретранслятора в ненагруженном резерве. Переключающее устройство предполагается абсолютно надежным. Командная система имеет постоянное резервирование. Системы питания, ориентации и телеметрии резерва не имеют. Заданы интенсивности отказа: каждого комплекта ретранслятора - l 1 , командной системы - l 2 , системы телеметрии - l 3 , системы питания - l 4 и системы ориентации - l 5 . Требуется определить вероятность безотказной работы Pc(t) бортовой аппаратуры спутника. Логическая схема для расчета надежности бортовой аппаратуры спутника представлена на рис. 8. Здесь I - аппаратура ретранслятора, II - командная система, III - остальные системы.
I II III
 |
Рис. 8
Решeниe.
Вероятность безотказной работы системы равна:
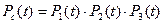
блок 3 – без резервирования (n=3);
блок 1 – резервирование замещением в режиме ненагружаемого резерва;
блок 2 – режим постоянного резервирования (m=1).
Для блока 1 вероятность безотказной работы равна:
.
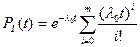Из условия задачи:
,
m = 1.
Тогда 
.
Для блока 2 вероятность безотказной работы равна:
,
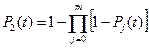где Pj - вероятности безотказной работы элемента резервного элемента j
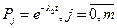
m =1.
Тогда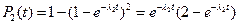 
Для блока 3 вероятность безотказной работы равна:
,
где 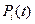- вероятности безотказной работы i -го элемента блока 3.
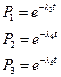
Тогда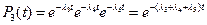 
.
Найдем вероятности безотказной работы системы:
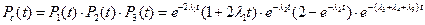
Ответ: 
Расчет показателей надежности резервированных устройств с учетом восстановления.
Задача 9.11 Система связи содержит одно устройство, предназначенное для выполнения задачи и одно устройство в нагруженном резерве. Интенсивность отказов каждого устройства равна l 1/час, восстановления - m 1/час. Ремонт устройств производится независимо друг от друга. Определить функцию готовности.
Решeниe.
2l l
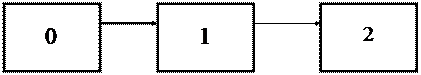
m 2m 
Рис. 9
Вычислительное устройство в любой момент времени может находиться в одном из следующих состояний:
0 - оба блока работоспособны;
1 - один блок неработоспособен;
2 - оба блока неработоспособны.
Схема состояний устройства представлена на рис.9. Определяем вероятность непрерывной безотказной работы в течении времени t. Система дифференциальных уравнений, полученная по схеме состояний, имеет следующий вид:
-lP0(t) + mP1(t);
lP0(t) - (l + m)P1(t);
lP1(t).
Начальные условия:
P0(0) = 1; P1(0) = P2(0) = 0.
При помощи преобразования Лапласа получаем систему алгебраических уравнений относительно изображений:
(s+l)P0(s) - mP1(s) = 1;
-lP0(s) + (s + l + m)P1(s) = 0;
-lP1(s) + sP2(s) = 0.
Путем решения этой системы либо подстановкой, либо по правилу Крамера получим
Раскладывая P2(s) на элементарные дроби и производя обратное преобразование Лапласа, определяем вероятность P2(t) попадания за время (0, t) в состояние 2
где обозначено
Следовательно, вероятность непрерывной безотказной работы вычислительного устройства за время (0, t) равна
