Определение оптимальных кратностей резервирования устройств и минимальной стоимости изделия

 

Вероятность безотказной работы i-го элемента за заданное время t в случае нерезервированного устройства:

P_i(0) = e ^–λit;

Вероятность безотказной работы i-го элемента за заданное время t при однократном резервировании (m_i=1):

P_i(1) = e ^–λit · (1 + λ_it);

Вероятность безотказной работы i-го элемента за заданное время t при двукратном резервировании (m_i=2):

P_i(1) = e ^–λit · (1 + λ_it+(λ_it)²/2);

Решение задачи оптимизации удобнее выполнить градиентным методом – методом наискорейшего спуска.

Значения показателя надежности устройств.

 

t_тр = 6000 ч.

 

mi	P1	P2	P6	P8
	0,8414	0,8624	0,6898	0,6173
	0,9868	0,99	0,9459	0,9151
	0,9992	0,9995	0,9935	0,9869

«Удельное» увеличение надёжности.

После добавления первого резервного устройства «удельное» увеличение надежности равно:

δ_i(1) = ;

После добавления второго резервного устройства «удельное» увеличение надежности равно:

δ_i(2) = .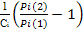

 

С₁=1,5; С₂=2,2; С₆=1,0; С₈=5,0.

 

mi	δ1	δ2	δ6	δ8
	0,1151	0,0672	0,3713	0,0965
	0,0085	0,0044	0,0503	0,0157

 

Составим последовательность всех δ_i по мере их убывания:

δ₆(1)> δ₁(1)> δ₈(1)> δ₂(1)> δ₆(2)> δ₈(2)> δ₁(2)> δ₂(2).

В соответствии с этой последовательностью осуществляют многошаговый процесс оптимального резервирования. Сначала вычисляют надежность без резервирования.

P_треб.(t)= 0,94.

P(t)= P₁(0) P₂(0) P₆(0) P₈(0)= 0,3063 < P_треб.(t);

P(t)= P₁(0) P₂(0) P₆(0) P₈(1)= 0,4962 < P_треб.(t);

P(t)= P₁(0) P₂(0) P₆(1) P₈(1)= 0,6281 < P_треб.(t);

P(t)= P₁(0) P₂(1) P₆(1) P₈(0)= 0,721 < P_треб.(t);

P(t)= P₁(1) P₂(1) P₆(1) P₈(1)= 0,8455 < P_треб.(t);

P(t)= P₁(1) P₂(1) P₆(1) P₈(2)= 0,9119 < P_треб.(t);

P(t)= P₁(1) P₂(1) P₆(2) P₈(2)= 0,958 > P_треб.(t).

Выбранные кратности резервирования обеспечивают требуемую надежность при минимальной стоимости изделия.

Логическая схема изделия с принятым оптимальным резервированием: