Физическая величина Х может быть при помощи математических действий выражена через другие физические величины А, В, С … уравнением вида:
Х= k Аa Вb Сg …,
где  - коэффициент пропорциональности;
- коэффициент пропорциональности;  - показатели степени.
- показатели степени.
Формулы вида (2), выражающие одни физические величины через другие, называются уравнениями между физическими величинами. Коэффициент пропорциональности в таких уравнениях за редким исключением равен 1. Значение этого коэффициента не зависит от выбора единиц, а определяется только характером связи величин, входящих в уравнение.
Для каждой системы величин число основных величин должно быть вполне определенным и его стараются свести к минимуму. Основные величины могут выбираться произвольно, но важно, чтобы система была удобной для практического применения. Как правило, в качестве основных выбирают величины, характеризующие коренные свойства материального мира: длину, массу, время, силу, температуру, количество вещества и др. Каждой основной величине присвоен символ в виде прописной буквы латинского или греческого алфавита, называемой размерностью основной физической величины. Например, длина имеет размерность L, масса — М, время — Т, сила тока — I и т. д.
Понятие размерности вводится и для производной величины.
Размерностью производной физической величины называется выражение в форме степенного одночлена, составлен-ного из произведений символов основных величин в различных степенях и отражающее связь данной физической величины с физическими величинами, принятыми в данной системе величин за основные, с коэффициентом пропорциональности, равным 1. Степени символов основных величин, входящих в одночлен, могут быт целыми, дробными, положительными и отрицательными в зависимости от связи рассматриваемой величины с основными. Связь производной величины через другие величины системы выражается определяющим уравнением производной величины. Размерность производной величины определяется путем подстановки в определяющее уравнение вместо входящих в него величин их размерностей. Причем, для этого используются простейшие уравнения связи, которые могут быть представлены в виде формулы (2). Например, если определяющим уравнением для скорости  является уравнение
является уравнение  , где
, где  —
—  длина пути, пройденного за время
длина пути, пройденного за время 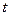 , то размерность скорости определяется по формуле
, то размерность скорости определяется по формуле  .
.
Форма уравнений, связывающих величины, не зависят от размеров единиц: какие бы единицы мы не выбирали, соотношения величин останутся неизменными и одинаковыми с соотношениями числовых значений. Этим свойством измерение отличается от всех других приемов оценки величин.
Размерность величин обозначается символом dim. В нашем случае размерность скорости будет выражена как

Например, в системе величин LMT (длина, масса, время) размерность любой величины Х в общем виде будет выражаться формулой:

где L, M, T — символы величин, принятых в качестве основных, в данном случае это длина, масса и время;  показатели размерности производной величины х.
показатели размерности производной величины х.
Размерность является более общей характеристикой, чем уравнение связи между величинами, т.к. одну и ту же размерность могут иметь величины разной природы, например, сила и кинетическая энергия.
Размерности имеют широкое практическое применение и позволяют:
- переводить единицы из одной системы в другую;
- проверять правильность расчетных формул;
- оценивать изменение размера производной величины при изменении размеров основных величин.






