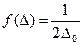y=F(x1, x2, …, xn), где x1, x2, …, xn – результаты прямых измерений со случайной ошибкой.
Известна функция F, связывающая y с x. Нужно найти мат.ожидание mу и sу. Обрабатывают результаты прямых измерений и находят математические ожидания m1, m2, …, mn и их отклонения s1, s2,..., sn или их оценки (S).
Правила.
1. my=F(mx1, mx2, …, mxn)
2. Если аргументы независимы, то определяют дисперсию 
, индекс m означает, что частные производные вычисляются в точках, где аргумент равен математическому ожиданию.
Пример 1.
Рассмотрим сумму и разность двух величин
1. y=х1 + х2; my=m1 + m2
s2y=s21 + s22 - для случая независимых аргументов.
Если х1 и х2 коррелированны, т.е. зависят друг от друга, то 
, где r - коэффициент корреляции; отклонения суммируются алгебраически с учетом знаков. Если Dx2 прямо пропорционален Dx1, то r=+1, sy=s1+s2. Если х1 возрастает и при этом х2 линейно убывает, то r=-1, sy=|s1+s2|.
Пример 2.
, 
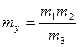, считая, что погрешности независимы имеем: 
Если разделим выражение на 
, то получим выражение 
;
- относительная среднеквадратичная погрешность 
. Для произведения и частного несколько величин изменяются со случайной ошибкой. Квадрат относительной ошибки результата равен сумме квадратов относительных величин. Чтобы найти доверительный интервал у нужно знать закон распределения х. Уже для трех аргументов это сложная задача и часто закон распределении неизвестен и используют Рд=0.9, для которого большинство распределений пересекаются в узком диапазоне и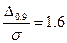 
.
Чтобы оценить погрешность, которая вносит прибор в результат измерения пользуются нормированием или предельными значениями погрешностей. Класс точности – характеристика, определяющая значение основных и дополнительных погрешностей. Согласно ГОСТу для определения класса точности используют определенный ряд чисел: 6 - 4 - 2,5 - 1,5 - 1,0 - 0.5 - 0,2 - 0,1 - 0,05 - 0,02 - 0,01 - … Значение класса точности маркируется на шкале прибора и записывается в техпаспорте. В соответствии классу точности определяют при проверках.
Систематические погрешности. Случайные погрешности. Законы распределения случайных погрешностей. Определение доверительных границ погрешностей для нормального закона распределения.
Систематические погрешности - постоянные или закономерно изменяющиеся погрешности.
Их основной отличительный признак: они могут быть предсказаны или устранены введением поправок.
Постоянные погрешности определяют при поверке по образцовым мерам или сигналам.
Закономерно изменяющиеся погрешности – большинство дополнительных погрешностей. Дополнительные погрешности устраняют схемной коррекцией.
Прогрессирующие погрешности – непредсказуемые погрешности медленно изменяющиеся во времени. Они вызываются старением деталей и их можно скорректировать только на данный момент времени, т.е. они требуют непрерывного повторения коррекции.
Случайные погрешности – вызываются несколькими причинами неподдающимися анализу. Их обнаруживают при повторных измерениях в виде разброса результатов.
Случайные погрешности проявляются при повторных измерениях одной и той же величины в виде разброса показаний. Оценку СП проводят с помощью теории вероятности.
Полным описанием случайной величины является ее закон распределения. Он может быть задан в интегральной или дифференциальной форме.
Часто СП подчиняются закону Гауса (нормальный закон распределения).
|
- плотность распределения вероятности СП D.
s - средне квадратичное отклонение.
При увеличении s кривая становится более плоской.
|
|
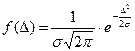
Основные характеристики законов распределения – математическое ожидание m и дисперсия D.
Математическое ожидание ряда измерений будет истинное значение измеряемой величины. Систематическая погрешность смещает математическое ожидание.
Дисперсия ряда измерений характеризует степень рассеяния результатов отдельных измерений вокруг математического ожидания. Чем меньше дисперсия, тем точнее измерения. Т.к. D измеряется в квадрате измеряемой величины, то применяют: 
.
m и D можно определить, если произведено большое число измерений (
).
Если число измерений n <20, то определяют оценку m и D.
Допустим провели ряд измерений и получили a1, a2, a3, …, an, где ai – результаты отдельных измерений, n – число измерений.
, 
- средне арифметическое.
При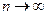 
Рассчитаем остаточные погрешности r: 
…
Оценка дисперсии ряда наблюдений подсчитывается:
Если , то 
и 
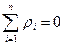- если отсутствует систематическая погрешность.
Если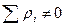 
, то из ряда измерений вычитают систематическую погрешность и ряд называется исправным.
Из теории вероятности известно, что 
- дисперсия средне арифметического в n-раз меньше дисперсии ряда измерений или 
- средне квадратичное отклонение в 
меньше средне квадратичного отклонения ряда измерений.
Погрешность дискретности подчиняется равномерному закону распределения.
|
|
|
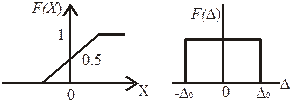
Если известен закон распределения, то можно определить вероятность появления погрешности D не выходящей за пределы некоторой границы. Этот интервал называется доверительным, а его вероятность доверительной.
В метрологии доверительная вероятность: Рд=0.9; 0.95
В теории надежности: Рд=0.8.
|
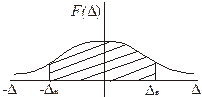
Для нормального закона распределения можно записать:
, где 
- функция Лапласса.
Ф(0)=0, Ф(-х)=-Ф(х) - свойства функции Лапласса.
Часто нужно найти вероятность того, что СП по абсолютному величине меньше заданного положительного числа e:
Найдем вероятность того, что 
Правило трех s.
Считают невозможным выход случайной ошибки за пределы трех s, т.е. в 997 из 1000 случаев погрешность не превосходит трех s.
Если погрешность больше трех s, то результат этого измерения называется промахом, и его отбрасывают.
Если случайная ошибка распределена по нормальному закону и n<20, то истинное значение измеряемой величины находят с использованием закона Стьюдента.
.
Коэффициент t берут из таблицы распределения Стьюдента.
В результат измерения входит не исключаемая систематическая погрешность q и случайная погрешность.
Если 
, то пренебрегают q и считают, что погрешность только случайная.
Если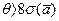 
, то пренебрегают СП, т.е.остается только систематическая погрешность.
Если 
, то границы погрешности находят по формуле из справочника.
