Неопределенность измерений

Понятие «неопределенность измерений» введено в практику описания точности средств измерений взамен термина «погрешность измерений». Неопределенность измерений - это параметр, связанный с результатом измерения, который характеризует рассеяние значений, которые могли бы быть обоснованно приписаны измеряемой величине. [4] Основное различие двух терминов состоит в том, что оценка точности дается не по отклонению от «истинного значения» величины (погрешность) а по разбросу значений, которые могут с определенной вероятностью быть приписаны результату измерений (неопределенность). Важной особенностью концепции «неопределенность измерения» является то, что составляющие неопределенности классифицируются не по природе их возникновения (как систематическая и случайная погрешность), а по методу их определения. Составляющие, определенные путем статистической обработки многократных измерений относятся к типу А, составляющие, определенные другими методами – к типу В. Все составляющие перечня неопределенностей называются «стандартные неопределенности», подчеркивая тем самым что они выражены в терминах среднего квадратического отклонения (СКО) соответствующих распределений и что при расчете суммарной неопределенности различие в методах (типах) их определения стирается и все составляющие имеют при сложении один статус.

Практические рекомендации по применению неопределенности измерений установлены в РМГ 43 – 2001 «Государственная система обеспечения единства измерений. Применение «Руководства по выражению неопределенности измерений».

Основным количественным выражением неопределенности измерения является стандартная неопределенность (u) и суммарная стандартная неопределенность (u_c). В тех случаях, когда это необходимо, вычисляют расширенную неопределенность U = k×u_c, где k - коэффициент охвата (числовой коэффициент, используемый как множитель суммарной стандартной неопределенности для получения расширенной неопределенности). Между характеристиками погрешности измерения и неопределенностями измерений существует определенное соответствие: СКО соответствует стандартной неопределенности, доверительные границы - расширенной неопределенности (рисунок 1).

При вычислении неопределенности измерений следует придерживаться последовательности:

1 Составление модели неопределенности (математическое моделирование процесса измерения)

Y = f (X₁,…, X_m). (1)

 

 

СКО, характеризующее случайную погрешность		Стандартная неопределенность, вычисленная по типу А
СКО, характеризующее неисключенную систематическую погрешность		Стандартная неопределенность, вычисленная по типу В
СКО, характеризующее суммарную погрешность		Суммарная стандартная неопределенность
Доверительные границы погрешности		Расширенная неопределенность

 

Рисунок 1 - Сопоставление оценок характеристик погрешности и неопределенностей результатов измерений

 

2 Определение оценок x₁,…, x_m входных величин X₁,…, X_m,внесение поправок на известные систематические факторы, возникающие в процессе измерения.

3 Определение оценки y результата расчета измерения выходной величины Y.

y = f (x₁,…, x_m). (2)

4 Определение стандартных неопределенностей u (x_j) входных величин X₁,…, X_m.

Стандартные неопределенности u (x_j) входных величин X₁,…, X_m определяют, либо с помощью статистических методов (стандартная неопределенность по типу А), либо иными методами (стандартная неопределенность по типу В).

4.1 Стандартная неопределенность по типу А u_А (x_j) j -й входной величины X_j выражается в виде СКО от среднеарифметического значения j -й входной величины X_j, вычисленной по формуле:

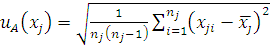, (3)

где n_j – количество единичных наблюдений j -й входной величины X_j;

i – порядковый номер единичного наблюдения j -й входной величины X_j;

x_ji – численное значение (результат) i -го единичного наблюдения j- й входной величины X_j.

4.2 Стандартная неопределенность по типу В u_В (x_j) j -й входной величины X_j, в случае, когда она является неисключенной систематической погрешностью, вычисляется по формуле:

, (4)

где θ_j – границы неисключенной систематической погрешности j -й входной величины X_j;

α_j – коэффициент, соответствующий принятому для данной j -й входной величины X_j закону распределения (нормального, равномерного, треугольного) внутри границ ± θ_j.

Для равномерного распределения α_j = , а для нормального α_j = 2 (при вероятности р = 0,95).

Стандартная неопределенность по типу В, зависит от закона распределения. При условии неполноты сведений о возможных значениях j -й входной величины X_j, чаще всего допускают, что они распределяются по равномерному (прямоугольному) закону в заданных границах относительно оценки x_j этой самой величины X_j. При этом стандартная неопределенность по типу В представляет собой оценку СКО.

5 Попарная корреляция (или статистическая зависимость) оценок x₁, …, x_m соответствующих входных величин X₁, …, X_m выражается с помощью коэффициентов корреляции.

Коэффициент корреляции r (x_j, x_k) оценок x_j и x_k j -й и k -й входных величин X_j и X_k соответственно выражает их статистическую зависимость, является безразмерной величиной и находится в пределах от минус 1 до 1 включительно. При r (x_j, x_k) = 0 корреляция отсутствует. При зависимости обеих оценок x_j и x_k входных величин X_j и X_k только от одной переменной коэффициент корреляции r (x_j, x_k) =1 или r (x_j, x_k) = –1.

Для вычисления коэффициента корреляции r (x_j, x_k) используют согласованные пары измерений (x_jl, x_kl) (где l = 1; …, n_kj; n_kj - число согласованных пар результатов измерений):

, (5)

где x_jl и x_kl – согласованная пара результатов измерений j -й и k -й входных величин X_j и X_k соответственно;

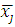и – среднеарифметические значения j -й и k -й входных величин X_j и X_k соответственно.

6 Вычисление суммарной стандартной неопределенности u_c (y)

6.1 В случае отсутствия корреляции между оценками x₁, …, x_m входных величин X₁, …, X_m, суммарная стандартная неопределенность u_c (y) выходной величины Y определяется по формуле:

, (6)

где u (x_j) – стандартная неопределенность, j- й входной величины X_j, вычисленная по типу А или В.

6.2 При наличии корреляции между оценками x_j и x_k соответствующих входных величинам X_j и X_k суммарная стандартная неопределенность u_c (y) выходной величины Y определяется по формуле:

, (7)

где r (x_j, x_k) - коэффициент корреляции;

u (x_j) и u (x_k) – стандартные неопределенности j- й и k -й входных величин X_j и X_k, вычисленные по типу А или В.

7 Расширенную неопределенность измерения U получают путем умножения суммарной стандартной неопределенности u_с (y) измеряемой величины Y на коэффициент охвата k:

. (8)

В общем виде коэффициент охвата k выбирают в соответствии с формулой

, (9)

где - квантиль распределения Стьюдента с эффективным числом степеней и доверительной вероятностью р. Значения коэффициента приведены в Приложении А.

Эффективное число степеней свободы определяют по формуле

, (10)

где - число степеней свободы при определении оценки j-й входной величины, при этом для вычисления неопределенностей по типу А, для вычисления неопределенностей по типу В [4].

Часто на практике для упрощения вычисления неопределенности результатов измерений делают предположение о нормальности закона распределения возможных значений измеряемой величины Y и полагают, что k = 2 при p = 0,95 или k = 3 при p = 0,99. Если же предполагают равномерность закона распределения, то k = 1,65 при p = 0,95 или k = 1,71 при p = 0,99 [4].

8 Полный результат измерения должен содержать в себе оценку значения y выходной величины Y и значение расширенной неопределенности измерения U с указанием доли p ожидаемых значений, которые могли бы быть обосновано ей (выходной величине) приписаны:

, р = … (11)

Данная запись буквально означает следующее: большая доля (р) ожидаемых значений, которые могли бы быть обосновано приписаны к измеренной величине Y, находятся в интервале от (y – U) до (y + U).

Пример вычисления неопределенности измерения приведен в Приложении Б.