Задание: выбрать посадку зубчатого колеса на вал диаметром 34 мм, провести вероятностный расчет посадки.
Выбор посадки зубчатого колеса на вал определяются условиями работы передачи, точностью передачи, условиями сборки узла. Для колёс, перемещаемых вдоль оси вала, применяют посадки Н7/g6; H7/h6, для неподвижных колёс – H7/js7; H7/k6. При значительных скоростях и динамических нагрузках рекомендуются посадки H7/n6; Н7/р6; H7/s6. Для тихоходных колёс невысокой точности (9...10 степени точности) применяют посадки H8/h7; H8/h8.
В данном примере выбираем переходную посадку Ø34H7/k6, которая позволит обеспечить точность центрирования сопрягаемых деталей, возможность самоустановки колеса под нагрузкой, легкость сборки и разборки соединения.
Рассчитываем предельные размеры отверстия Ø34Н7.
По ГОСТ 25346 определяем значения допуска IT7 = 25 мкм и основного (нижнего) отклонения EI = 0 мкм.
Верхнее отклонение будет равно
ES = EI + IT9 = 0 + 25 = +25 мкм.
Предельные размеры отверстия:
Dmin = D0 + EI = 34,000 + 0 = 34,000 мм;
Dmax = D0 + ES = 34,000 +0,025 = 34,025 мм.
Рассчитываем предельные размеры вала Ø34k6.
По ГОСТ 25346 определяем значения допуска IT6 = 16 мкм и основного (нижнего) отклонения ei = +2 мкм.
Верхнее отклонение будет равно
es = ei + IT6 = +2 + 16 = +18 мкм.
Предельные размеры вала:
dmin = d0 + ei = 34,000 + 0,002 = 34,002 мм;
dmax = d0 + es = 34,000 + 0,018 = 34,018 мм.
Результаты расчётов оформим в виде таблицы.
Таблица 2 - Расчёт предельных размеров деталей сопряжения
| Размер | IT, мкм | ES (es), мкм | EI (ei), мкм | Dmin (dmin), мм | Dmax (dmax), мм |
| Æ34Н7 | + 25 | 34,000 | 34,025 | ||
| Æ34k6 | + 18 | + 2 | 34,002 | 34,018 |
Строим схему расположения полей допусков сопрягаемых деталей и рассчитываем предельные значения табличных зазоров (натягов).
Dcp = (Dmax + Dmin)/2 = (34,025 + 34,000)/2 = 34,0125 мм;
dcp = (dmax + dmin)/2 = (34,002 + 34,018)/2 = 34,010 мм;
Smax = Dmax – dmin = 34,025 – 34,002 = 0,023 мм;
Nmax = dmax – Dmin = 34,018 – 34,000 = 0,018 мм;
Допуск посадки
T(S,N) = ITD + ITd = 0,025 + 0,016 = 0,041 мм.
Принимаем нормальный закон распределения размеров и рассчитываем предельные значения вероятных зазоров (натягов). В рассматриваемом сопряжении Dcp > dcp,
поэтому в данном сопряжении будет большая вероятность возникновения зазоров.
Рассчитываем математическое ожидание и стандартное отклонение зазоров:
MS = Dcp – dcp = 34,0125 – 34,010 = 0,0025 мм;
.
Примечание. Если средний диаметр отверстия меньше среднего диаметра вала, то в сопряжении будет большая вероятность возникновения натягов. В этом случае рассчитывают математическое ожидание натягов. Если средний диаметр отверстия равен среднему диаметру вала, то в сопряжении будет одинакова вероятность возникновения зазоров и натягов. Математическое ожидание зазоров и натягов в этом случае равно нулю.
Рассчитаем предельные значения вероятных зазоров и натягов:
Smax.вер. = MS + 3s(S,N) = 2,5 + 3×4,9 = 17,2 мкм = 0,017 мм;
Smin.вер. = MS – 3s(S,N) = 2,5 – 3×4,9 = –12,2 мкм;
Nmax.вер = 12,2 мкм = 0,012 мм.
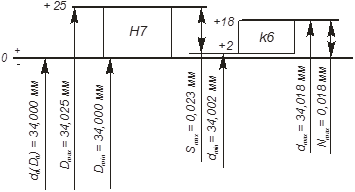Рисунок 3 - Схема расположения полей допусков сопрягаемых деталей
| 
Рисунок 4 - Распределение вероятных зазоров (натягов)
|
При применении переходных посадок в сопряжениях возможны зазоры или натяги. Поэтому рассчитываем вероятность их получения. Для определения площади, заключённой между кривой Гаусса, выбранными ординатами и осью абсцисс (на рис.4 заштрихована площадь, определяющая процент зазоров), удобно использовать табулированные значения функции (приложение 1).
,
где 
.
В данном примере
х = MS = 2,5 мкм;
s(S,N) = 4,9 мкм.
Тогда
z = MS/ s(S,N) = 2,5/4,9 = 0,51;
Ф(z=0,51) = 0,1950 = 19,5 % (см. приложение 1)
Таким образом, с учетом симметрии распределения (P" = = 0,5), вероятность получения зазоров в сопряжении Æ34Н7/k6 составляет
Р(S) = 50 % + 19,5 % = 69,5 %.
Определим вероятность получения натягов, принимая что 0,9973 ≈ 1
Р(N) = 30,5%.
