Відомо, що похибка вимірювання складається з систематичної та випадкової. Систематичну складову похибку можна визначити по формулам, графікам, діаграмам і т.п.
Випадкова похибка вимірювального приладу це складова основної похибки, що змінюється випадково по законам, що невідомі експериментатору.
Для оцінки випадкових похибок досить визначити числові характеристики – математичне сподівання та середньоквадратичне відхилення, але значення цих характеристик можливо обчислити тільки при нескінченному числі вимірювань. Практично число вимірювань n завжди обмежене і тому в цьому випадку обчислюють наближені оцінки математичного сподівання та середньоквадратичного відхилення.
Для визначення складової випадкової похибки виконують n (n ³10) рівноточних спостережень. Ці спостереження називають ще рівнорозсіяними, якщо вони є незалежними, однаково розподіленими випадковими величинами. Експериментатор повинен виконувати вимірювання при незмінних умовах (температурі і вологості повітря, частоті та напрузі мережі, зовнішніх магнітних полях) і тими самими приладами.
Гіпотеза про нормальне розподілення результатів випадкових спостережень приймається без перевірки.
Статистична обробка групи результатів спостережень при рівноточних вимірюваннях та нормальному розподілу виконується в такій послідовності. Обробку проміжних результатів доцільно записувати в таблицю 2.1, кількість строчок в якій відповідає кількості спостережень.
Таблиця 2.1
Результати обробки ряду спостережень
| хі | х¢і | х¢і ¯ | 
| ρ і | ρ і 2 | s | n і | S 
| D дов |
Прийняті позначки
хі – результат і -того спостереження (графа 1);
х¢і – виправлений результат, який одержуємо після виключення систематичної похибки DС із результатів спостережень
(графа 2) (2-1).
В 3 графу записати виправлені результати спостережень у неспадній послідовності х¢1 ¯ £ х¢2 ¯ £ х¢3 ¯... £ х¢n ¯
Середньоарифметичне значення ряду спостережень виправлених результатів
(графа 4) (2-2).
Цю величину приймають за оцінку результату вимірювання.
Випадкове відхилення ρ і виправленого результату окремого спостереження від середнього арифметичного виправлених результатів спостережень
(графа 5) (2-3).
При обробці результатів обчислень та ρі перевірити умову, що
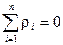
У графу 6 занести величину ρ і 2
Середньоквадратичне відхилення результату спостереження (СКВ) характеризує ступінь розсіяння результатів спостережень навколо середнього арифметичного значення
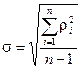, (графа 7) (2-4). Виключення з ряду спостережень анормальних результатів (грубих похибок).
Для цього необхідно обчислити коефіцієнти n1 і n n
, (графа 8) (2-5)
і порівняти їх з коефіцієнтом b (табл.2.2), що залежить від даного об’єму вибірки та прийнятого рівня значущості a.
a = 1 – P (2-6)
Таблиця 2.2
Граничне значення b при оцінці анормальності результату спостереження
| a | n | ||||||||||
| 0,05 | 1,15 | 1,46 | 1,67 | 1,82 | 1,94 | 2,03 | 2,11 | 2,18 | 2,23 | 2,29 | 2,33 |
| 0,1 | 1,16 | 1,42 | 1,60 | 1,73 | 1,83 | 1,91 | 2,03 | 2,03 | 2,09 | 2,13 | 2,17 |
Якщо n1<b та n n <b, всі спостереження вважаються нормальними.
Обчислити середньоквадратичне відхилення результату вимірювання
(графа 9) (2-9)
Довірчі межі випадкової похибки результату вимірювання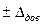 
– це межі інтервалу, в якому знаходиться випадкова похибка вимірювання із заданою ймовірністю.
Зв’язок 
з похибкою вимірювання неоднозначний і залежить від числа спостережень n, функції розподілу випадкових похибок та коефіцієнта розподілу Стьюдента t ( n ) (табл.2.3).
, (графа 10) (2-10)
Таблиця 2.3
Таблиця коефіцієнта t(n) розподілення Стьюдента
| P | n -1 | |||||||||
| 0,95 | 3,182 | 2,776 | 2,571 | 2,447 | 2,365 | 2,306 | 2,262 | 2,228 | 2,201 | 2,179 |
| 0,9 | 2,353 | 2,132 | 2,015 | 1,943 | 1,895 | 1,860 | 1,833 | 1,812 | 1,796 | 1,782 |
Результати вимірювань записати у стандартній формі:
.
Якщо n¢1³b та n¢ n ³b (або один з них), то результати спостережень х ¢1¯ та х ¢ n ¯ (або один з них), відповідно анормальні і їх необхідно виключити з ряду.
При зменшенні кількості спостережень в ряді треба знову обчислити , r і, s, n1, n n, дані розрахунків привести в новій таблиці і перевірити на наявність грубих похибок.
Примітка. Варіант завдання вибрати по номеру залікової книжки. Якщо номер залікової книжки більше 45, тоді варіант вибрати (№книжки – 45).
