Краткие методические указания по выполнению контрольной

РАБОТЫ

 

2.1. Тема «Методы обработки и оценки результатов измерений»

2.1.1. Выявление и исключение грубых погрешностей.

При однократных измерениях обнаружить промах не представляется возможным. Для уменьшения вероятности появления промахов измерения проводят два-три раза, и за результат принимают среднее арифметическое полученных значений. При многократных измерениях для обнаружения промахов используют статистические критерии, предварительно определив, какому виду распределения соответствует результат измерений.

Вопрос о том, содержит ли результат наблюдения грубую погрешность, решается общими методами проверки статистических гипотез. Проверяемая гипотеза состоит в утверждении, что результат наблюдений не содержит грубой погрешности, т.е. является одним из значений измеряемой величины. Пользуясь определенными статистическими критериями, пытаются опровергнуть выдвинутую гипотезу. Если это удастся, то результат наблюдений рассматривают как содержащий грубую погрешность и исключают.

Для выявления грубых погрешностей задаются вероятностью q – уровнем значимости того, что сомнительный результат действительно мог иметь место в данной совокупности результатов измерений.

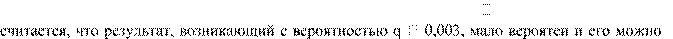Критерий «трех сигм» применяется для результатов измерений, распределенных по нормальному закону и достаточно надежен при числе измерений n 20. По этому критерию

 

 

 

считать промахом, если

x xi 3,

 

– оценка среднего квадратичного отклонения

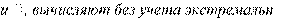измерений; – среднее арифметическое значение ряда измерений; Хi– результат измерения, вызывающий сомнение (обычно проверяют наибольшее Xmaxи наименьшее Xminзначения результатов измерений). Величины x ых значений хi.

В случае, если число измерений 3≤ n ≤ 25, применяется критерий Греббса – Смирнова или Романовского. При этом вычисляется отношение и сравнивается с

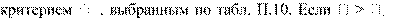, то результат хi считается промахом и

отбрасывается.

При числе измерений 2≤ n ≤ 10 применяется критерий Шовинэ. При этом если разность 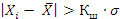, то результат измерений Хi отбрасывают как содержащий грубую погрешность. Коэффициент Кш определяется в зависимости от числа измерений n:

n
Кш	1,6	1,7	1,9	2,0

 

Более подробно ознакомиться с материалом по этому разделу и примерами расчетов можно по учебным пособиям [2, c.48…114], [4].

2.1.2. Методы обработки результатов измерений

Результаты измерений, выполненных в разных условиях, разными операторами или в разное время подлежат проверке на равноточность.

Пример 1.

В результате работы пункта технического осмотра (ПТО) грузовых вагонов были получены выборки и выявлены вероятности появления дефектов ходовых частей, подчиняющиеся нормальному закону распределения.

При этом выборка для смен, работающих в ночное время, была получена за

n 1 = 12

смен, и характеризуется она средним арифметическим значением вероятности обнаружения

дефектов Х 1

= 6,4 %, а также среднеквадратическим отклонением 1 = 0,97 %.

Данные для полученной выборки работы дневной смены характеризуется средним

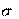арифметическим значением вероятности обнаружения дефектов среднеквадратическим отклонением 2 = 0,75 %, и накоплены они за

Х 2 = 7,1 %,

n 2 = 11 смен.

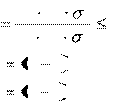
Двухвыборочный t – критерий Стьюдента используется в случае, когда сравниваемые выборки подчиняются нормальному закону распределения и при этом обеспечивается условие равенства их дисперсий. Гипотеза о равенстве дисперсий в выборках проверяется сравнением частных несмещенных значений генеральной совокупности следующим образом:

Fрасч

п 1 k 2 F

a

n 2 k 1 2

где k 2 n 2

k 1 n 1

1 – степень свободы для значения в числителе;

1 – степень свободы для значения в знаменателе;

Fa – критическая область значимости для исследуемого распределения.

В нашем случае для

k 1 =12 – 1= 11 и k 2

=11 – 1= 10 по таблице F –распределения

(прил. 3) найдем значение Fa

F 0,05= 2,94.

12 10 0,97

1,283

2,94

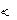Соответственно,

Fрасч

11 11 0,75

Условие

Fрасч < Fa

соблюдается, что свидетельствует о том, что существенной разницы

между дисперсиями в исследуемых выборках нет и их можно сравнить, используя двухвыборочный t – критерий Стьюдента.

Нахождение t – критерия является наиболее часто используемым методом обнаружения сходства между средними значениями двух выборок. Значение данного критерия находится из условия:

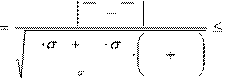Х 1 Х 2

t ta

k 2 k 2 1 1

1 1 2 2

k n 1 n 2

 

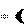где

ta – сравнительный показатель, который зависит от уровня значимости

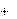ka n 1 n 2

2 и находится из прил. 2.

Подставляя данные, находим:

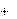ka 12 11 2 21

 

Из прил. 2

ta =

t 0,05

 

= 2,08

Тогда значение t – критерий Стьюдента:

 

t

11 0,972

6,4

10

7,1

0,752 1 1

12 11

 

1,9227

Т.к. условие t = 1,9227 <

ta = 2,08 соблюдается, то сравниваемые выборки равны, а

разница между ними случайна и причины ее несущественны. Соответственно, статистическое сравнение данных выборок работы пункта технического осмотра (ПТО) в ночную и дневную смены возможно. Также возможно объединение накопленных данных в одну общую выборку, которая позволит получить достоверные данные о вероятности обнаружения дефектов ходовых частей грузовых вагонов в процессе работы ПТО в течение суток.

3.1.3. Методы оценки точности измерений

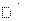Для обоснованной оценки точности многократных измерений (n>40) и выбора доверительных границ результатов измерений необходимо выполнить проверку соответствия распределения случайных величин нормальному закону. В наибольшей степени этой цели соответствует критерий (критерий Пирсона). С примерами решения этой задачи можно ознакомиться в учебных пособиях [3, c.278…283], [4].

 

2.2. Тема «Экономическая эффективность стандартизации»

Экономическую эффективность стандартизации в каждом частном случае необходимо рассматривать комплексно, с учетом всех экономических, технических и организационных сторон. С помощью стандартов и других нормативных документов ограничивается неоправданное разнообразие продукции, материалов, технологических процессов; устанавливается рациональная их номенклатура; определяются оптимальные параметрические и размерные ряды; обеспечивается высокий уровень взаимозаменяемости; устанавливаются в качестве обязательных оптимальные качественные характеристики. Все это создает предпосылки для специализации и автоматизации производственных процессов, снижения себестоимости продукции и услуг и, следовательно, увеличения прибыли.

Экономический эффект от внедрения стандартов может быть реализован в двух направлениях:

повышение качества продукции и услуг;

снижение затрат на проектирование, производство, эксплуатацию продукции и оказание услуг.

Пример 2.

Расчетные минимальные геометрические размеры транспортного пакета для перевозки груза равны a = 525 мм, b = 410 мм, c = 345 мм. Используемый контейнер – УК-3.

Решение:

Транспортным пакетом называется укрупненное грузовое место, сформированное из отдельных мест груза в таре (например, ящиках, мешках, бочках, специализированных контейнерах) или без тары, скрепленных между собой с помощью универсальных, специальных разового использования или многооборотных пакетирующих средств, на поддонах или без них. Размеры и конструкция тары должны обеспечивать наилучшее использование грузоподъемности и вместимости вагонов (контейнеров).

На основе рядов предпочтительных чисел

Ra 5,

Ra 10,

Ra 20 и

Ra 40

проведем

обоснование геометрических размеров транспортного пакета для перевозки груза.

При изготовлении транспортного пакета по ряду предпочтительных чисел размеры транспортного пакета будут равны a = 630 мм, b = 630 мм, c = 400 мм.

При изготовлении транспортного пакета по ряду предпочтительных чисел размеры транспортного пакета будут равны a = 630 мм, b = 500 мм, c = 400 мм.

При изготовлении транспортного пакета по ряду предпочтительных чисел размеры транспортного пакета будут равны a = 560 мм, b = 450 мм, c = 360 мм.

При изготовлении транспортного пакета по ряду предпочтительных чисел размеры транспортного пакета будут равны a = 530 мм, b = 420 мм, c = 360 мм.

Ra 5 (прил.5.)

 

Ra 10(прил.5.)

 

Ra 20(прил.5)

 

Ra 40(прил.5)

По заданию используется контейнер УК-3, для которого длина равна 1980 мм, ширина

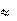
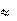
1225 мм и высота 2128 мм. При изготовлении по ряду

Ra 5

данных пакетов поместится: в длину

1980/ 630

3,142

3 пакета; в ширину 1225/630

1,944

1 пакет; в высоту

2128/ 400

5,32 5

ярусов транспортных пакетов. Итого при изготовлении транспортных пакетов по ряду

Ra 5 их

общее количество будет равно 3 1

5 = 15 пакетов.

При изготовлении по ряду

Ra 10

транспортных пакетов поместится: в длину

1980 / 630

3,142

3 пакета; в ширину

1225/ 500

2,45 2

пакета; в высоту

2128/ 400

5,32

5 ярусов транспортных пакетов. Итого при изготовлении транспортных

пакетов по ряду

Ra 10их общее количество будет равно 3 2

5 = 30 пакетов.

При изготовлении по ряду

Ra 20

транспортных пакетов поместится: в длину

1980/ 560

3,535 3

пакета; в ширину

1225/ 450

2,72 2

пакетам; в высоту

2128/ 360

5,91

5 ярусов. Итого их общее количество будет равно 3 2

5 = 30 пакетов. В

тоже время, если расположить пакеты более оптимально (в длину 1980/450

4,4

4 пакета; в

ширину пакетов.

1225/ 560

2,18

2 пакета), их общее количество будет равно 4

2 5 = 40

При изготовлении по ряду

Ra 40

транспортных пакетов поместится: в длину

1980/ 530

3,735 3

пакета; в ширину

1225/ 420

2,916

2 пакета; в высоту

2128/ 360

5,91

5 пакетов. Итого их общее количество будет равно 3 2

5 = 30 пакетов. В

тоже время, если расположить пакеты более оптимально (в длину 1980/420

4,71

4 пакета; в

ширину пакетов.

1225/ 560

2,18

2 пакета), их общее количество будет равно 4

2 5 = 40

Рис. 6 Схема расположения транспортных пакетов в контейнере

 

Анализируя проведенные расчеты, можно сделать вывод о том, что наиболее оптимальным по экономическим показателям является изготовление транспортного пакета для

перевозки груза по размерам из ряда

Ra 20 и

Ra 40. С учетом того, что в соответствии с

ГОСТ 6636-69 размеры из ряда

Ra 20

следует предпочитать размерам из ряда

Ra 40,

принимаем для изготовления транспортного пакета для перевозки груза размеры по ряду Ra 20. При этом, для достижения наибольшего экономического эффекта, необходимо разместить транспортные пакеты в контейнере по схеме, приведенной на рис. 6.

Экономическую эффективность изготовления изделий с размерами, назначенными по рядам предпочтительных чисел (ГОСТ 8032-84 или ГОСТ 6636-69), определяют по себестоимости годовой программы изделий [2, c. 486…498], [4].

 

2.3. Тема «Формы подтверждения соответствия».

Форма подтверждения соответствия определяет порядок документального удостоверения продукции или иных объектов технического регулирования требованиям технических регламентов, положениям стандартов или условиям договоров. Процедура подтверждения соответствия осуществляется согласно схемам, каждая из которых представляет собой полный набор операций и условий их выполнения участниками подтверждения соответствия [2, c. 610…638].