–езультаты наблюдений за надежностью машин и их элементов в том виде, как они получены по данным первичной учетной документации, представл€ют собой р€д неупор€доченных чисел, указывающих наработку изделий до отказов, ресурсы изделий и др.
¬ результате наблюдений получены следующие данные о наработке пакера ___1_____ (таблица). ѕод наблюдением находилось 50 изделий.
“аблица 1 Ц –езультаты наблюдений за надежностью оборудовани€
| Ќомер п/п | Ќаработка до отказа, ч | Ќомер п/п | Ќаработка до отказа, ч | Ќомер п/п | Ќаработка до отказа, ч | Ќомер п/п | Ќаработка до отказа, ч |
ћинимальное значение наработки равно 19 ч, максимальное 2180 ч.
«она рассеивани€ составл€ет
R = 2180 Ц 19 = 2161 ч.
ƒл€ определени€ числа интервалов используем формулу

¬еличина интервала 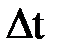 в рассматриваемом случае равна
в рассматриваемом случае равна
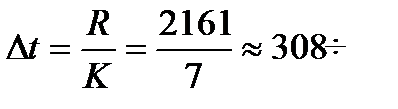 .
.
ќпредел€ем границы каждого интервала:
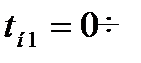 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,

 ,
,
 ,
,
ќпредел€ем середину каждого интервала по формуле  :
:
 ,
,
 ,
,
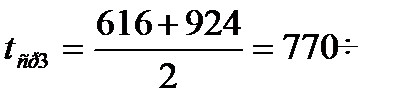 ,
,
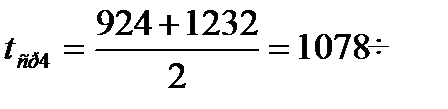 ,
,
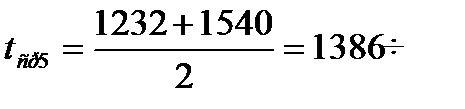 ,
,
 ,
,
 ,
,
ќпредел€ем число отказов, соответствующих каждому интервалу:
n1=24;
n2=14;
n3=5;
n4=1;
n5=2;
n6=1;
n7=3;
ќпредел€ем частоту отказов дл€ каждого интервала по формуле 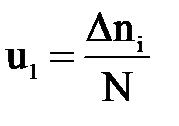 :
:
 ,
,
 ,
,
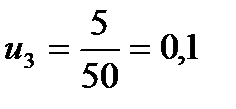 ,
,
 ,
,
 ,
,
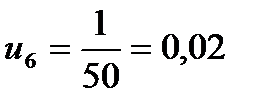 ,
,
 ,
,
–езультаты сводим в таблицу 2.
“аблица 2 Ц —татистический р€д информации
| Ќомер интервала i | »нтервал времени,  , ч , ч
| —ередина интервала  , ч , ч
| „исло отказов 
| „астота отказов 
|
| 0-308 | 0,48 | |||
| 308-616 | 0,28 | |||
| 616-924 | 0,1 | |||
| 924-1232 | 0,02 | |||
| 1232-1540 | 0,04 | |||
| 1540-1848 | 0,02 | |||
| 1848-2156 | 0,06 | |||
| »того | 1,00 |
3.2 –асчет параметров статистического распределени€
ћатематическое ожидание определ€ем по формуле:
 .
.
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
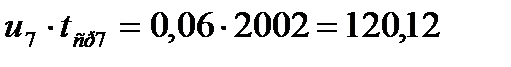 ,
,
ћатематическое ожидание составл€ет

ƒисперсию определ€ем по формуле:
 .
.
 ,
,
 ,
,
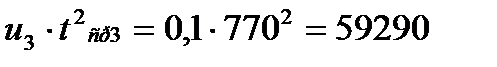 ,
,
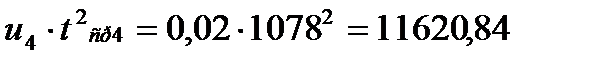 ,
,
 ,
,
 ,
,
 ,
,
ƒисперси€ составл€ет

—реднее квадратичное отклонение определ€ем по формуле:
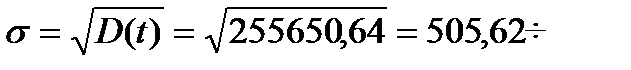 .
.
оэффициент вариации определ€ем по формуле:
|
|
|
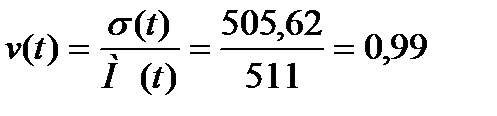 .
.
–езультаты расчета по вычислению числовых характеристик приведены в таблице 3.
“аблица 3 Ц ¬ычисление числовых характеристик
| Ќомер интервала i | »нтервал времени, 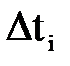 , ч , ч
| —ередина интервала  , ч , ч
| „астота отказов 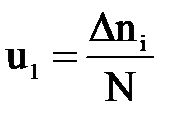
| 
| 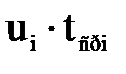
| 
|
| 0-308 | 0,48 | 73,92 | 11383,68 | |||
| 308-616 | 0,28 | 129,36 | 59764,32 | |||
| 616-924 | 0,1 | |||||
| 924-1232 | 0,02 | 21,56 | 11620,84 | |||
| 1232-1540 | 0,04 | 55,44 | 76938,84 | |||
| 1540-1848 | 0,02 | 33,88 | 57392,72 | |||
| 1848-2156 | 0,06 | 120,12 | 240480,24 | |||
| »того | 1,00 | 511,28 | 516870,64 |
3.3 ќценка резко выдел€ющихс€ статистических данных
јнализ резко выдел€ющихс€ статистических данных проводитс€ с целью проверки возможности их исключени€ из рассматриваемого р€да.
ќпредел€ем минимальное и максимальное значени€ наработки. ¬ы€вл€ем возможные факторы, обеспечившие сокращение или увеличение сроков работы оборудовани€: режимы и услови€ эксплуатации, применение новых технологий при ѕ“ќ, т.п.
¬ычисл€ем критерий √раббса:
 ,
,

3.4 ѕостроение эмпирических кривых распределени€
ќбъединим интервалы 3- 4 и интервалы 5-7, так как начина€ с п€того интервала число отказов мало (0-2). ¬ результате зона рассеивани€ разбиваетс€ на 6 интервалов:
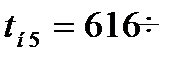 ;
;  ;
;  ;
;  ; ∆t=616;
; ∆t=616;
 ;
;  ;
; 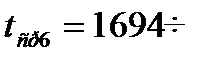 ;
;  ;∆t=924;
;∆t=924;
—татистическа€ оценка веро€тности безотказной работы оборудовани€ определ€етс€ выражением:
 .
.
ќпределим число отказавших изделий n(tсрi) к моменту времени tсрi:
 ,
,
 ,
,
 ,
,
 ,
,
ќпределим число исправных изделий N(tсрi) к моменту времени tсрi:
 ,
,
 ,
,
 ,
,
 .
.
—татистическа€ оценка веро€тности безотказной работы оборудовани€ определ€етс€ выражением:
 ,
,
 ,
,
 ,
,
 .
.
—татистическа€ оценка веро€тности отказа оборудовани€:
 .
.
 ,
,
 ,
,
 ,
,
 .
.
—татистическа€ частота отказов определ€етс€ выражением:
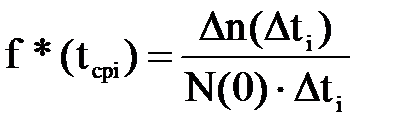 .
.




—татистическа€ интенсивность отказов определ€етс€ выражением:
 .
.


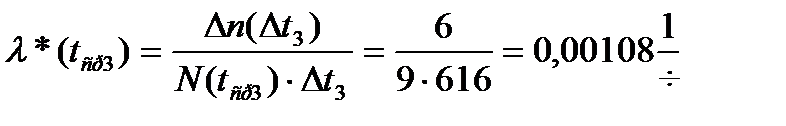

ƒанные расчетов приведены в таблице 4.
“аблица 4 Ц ќпределение статистических показателей надежности
| Ќомер интервала i | »нтервал времени, ∆ti, ч | —ередина интервала tсрi, ч | „исло отказавших изделий ∆ni за врем€ ∆ti | „исло отказавших изделий n(tсрi) к моменту времени tсрi | N(tсрi)=N(0)-n(tсрi) | 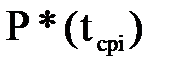
| 
| 
| 
|
| 0-308 | 0,77 | 0,24 | 0,00156 | 0,00205 | |||||
| 308-616 | 0,38 | 0,62 | 0,00091 | 0,00239 | |||||
| 616-1232 | 0,18 | 0,82 | 0,00019 | 0,00108 | |||||
| 1232-2156 | 0,06 | 0,94 | 0,00013 | 0,00216 |
ѕо данным таблицы 4 строим зависимости показателей безотказности  ,
,  ,
,  ,
,  .
.

–исунок 2 - —татистическа€ веро€тность безотказной работы

–исунок 3 Ц —татистическа€ веро€тность отказов оборудовани€
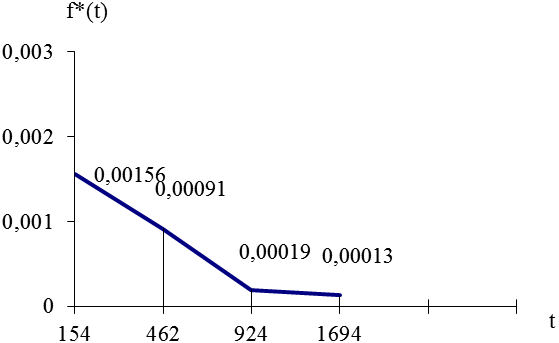
–исунок 4 - —татистическа€ частота отказов оборудовани€

–исунок 5 - —татистическа€ интенсивность отказов оборудовани€
3.5 ¬ыбор теоретического закона распределени€
ѕо виду кривых (–исунки 2, 3, 4, 5)выбираем экспоненциальный закон распределени€.
3.6 ќпределение параметров распределени€
ќпредел€ем теоретические показатели надежности 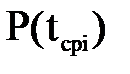 ,
,  ,
,  ,
,  .
.
|
|
|
ѕри экспоненциальном распределении примен€ем формулы:
¬еро€тность безотказной работы издели€ 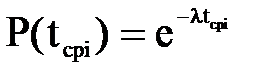
¬еро€тность отказа издели€ 
„астота отказов 
»нтенсивность отказов 
ƒл€ экспоненциального закона распределени€ необходимо прежде всего определить значение интенсивности.

«на€ параметр экспоненциального распределени€, можем найти значени€ характеристик надежности оборудовани€.
¬еро€тность безотказной работы издели€
 ,
,
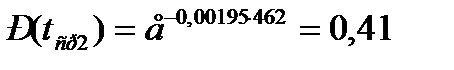 ,
,
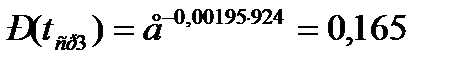 ,
,
 ,
,
¬еро€тность отказа издели€
 ,
,
 ,
,
 ,
,
 ,
,
„астота отказов
 ,
,
 ,
,
 ,
,
 ,
,
ƒанные расчетов сводим в таблицу 5.
“аблица 5 - ќпределение теоретических показателей надежности
| Ќомер интервала i | »нтервал времени, ∆ti, ч | —ередина интервала tсрi, ч | 
| 
| 
| 
|
| 0-308 | 0,74 | 0,26 | 0,001443 | 0,00195 | ||
| 308-616 | 0,41 | 0,59 | 0,0007995 | 0,00195 | ||
| 616-1232 | 0,165 | 0,835 | 0,000322 | 0,00195 | ||
| 1232-2156 | 0,037 | 0,963 | 0,000072 | 0,00195 |
3.7 ѕроверка гипотезы о соответствии эмпирического и теоретического законов распределени€
ƒл€ проверки гипотезы о законе распределени€ статистических данных применим критерий ѕирсона.
ритерий ѕирсона определ€ем по формуле:
 ,
,
где - количество интервалов наблюдени€.
 - эмпирические частоты случайной величины в заданном временном интервале, определ€етс€ по результатам наблюдений (таблица 4);
- эмпирические частоты случайной величины в заданном временном интервале, определ€етс€ по результатам наблюдений (таблица 4);
 - теоретические частоты случайной величины в том же интервале.
- теоретические частоты случайной величины в том же интервале.
«начени€ веро€тностей случайной величины на границах интервалов:
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
“еоретические веро€тности попадани€ случайной величины в i-ый интервал:
 ,
,
 ,
,
 ,
,
 ,
,
“еоретические частоты случайной величины:
 ,
,
 ,
,
 ,
,
 ,
,
ќпределим отклонени€ эмпирических параметров случайной величины от теоретических  -
-  :
:
 ,
,
 ,
,
 ,
,
 ,
,
—ледующий этап вычислений критери€ ѕирсона:
 ,
,
 ,
,
 ,
,
 ,
,
–езультаты вычислений приведены в таблице 6.
“аблица 6 - ќпределение критери€ ѕирсона
| Ќомер интервала i | »нтервал времени, ∆ti, ч | 
| 
| 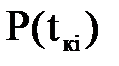
| 
| 
| 
| 
|
| 0-308 | 0,548 | 0,452 | 22,6 | 1,4 | 0,087 | |||
| 308-616 | 0,548 | 0,3008 | 0,2472 | 12,36 | 1,64 | 0,218 | ||
| 616-1232 | 0,3008 | 0,0905 | 0,2103 | 10,515 | -4,515 | 1,939 | ||
| 1232-2156 | 0,0905 | 0,0149 | 0,0756 | 3,78 | 2,22 | 1,304 |
ритерий ѕирсона равен:
 .
.
ќпредел€ем число степеней свободы
 ,
,
где s - число параметров теоретического распределени€, дл€ экспоненциального распределени€ s=1.
 .
.
ѕри данном уровне значимости и данном количестве наблюдений определ€ем, что  .
.
„исло степеней свободы r=2 и X2=3,548(таб.9) веро€тность совпадени€ теоретического и статического распределени€ –<0,5, что отвергает прин€тую нами гипотезу о распределении наработки пакера по экспоненциальному закону.
“.к.  , то расхождени€ между теоретическими и эмпирическими частотами считаем случайными, а теоретическое распределение показателей надежности - не противоречащим опытному.
, то расхождени€ между теоретическими и эмпирическими частотами считаем случайными, а теоретическое распределение показателей надежности - не противоречащим опытному.
3.8 ѕостроение теоретических кривых распределени€
ѕо данным таблицы 5 строим графики

–исунок 6 - “еоретическа€ веро€тность безотказной работы

–исунок 7 Ц “еоретическа€ веро€тность отказов оборудовани€

–исунок 8 - “еоретическа€ частота отказов оборудовани€

–исунок 9 - “еоретическа€ интенсивность отказов оборудовани€
3.9 ќпределение доверительных границ показателей надежности
ƒоверительные границы рассеивани€ среднего значени€ дл€ экспоненциального закона распределени€ определ€ем по формулам:
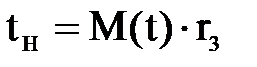 и
и 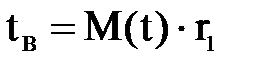 ,
,
где  , = 1,28 - коэффициент, определ€емый по таблице 12 [9]
, = 1,28 - коэффициент, определ€емый по таблице 12 [9]
 = 0,8 - коэффициент, определ€емые по таблице 13 [9].
= 0,8 - коэффициент, определ€емые по таблице 13 [9].








