Одним из основных (инженерных) методов является метод, основанный на использовании понятия графа переходов между состояниями.
Этот метод распадается на два вида:
1) Граф интенсивности перехода. Основное условие использования этого метода это то, что потоки событий простейшие, т.е. отказы и восстановления описываются экспоненциальными законами;
2) Метод переходных матриц вероятностей. В принципе, может быть любой закон распределения вероятности, но инженерное использование его проблематично.
3.2. Метод графа интенсивности перехода
По Колмогорову-Чепмену (в основе метода лежит граф состояний).
Рис. 9. Граф состояний.
1. Устройство в рабочем состоянии;
2. Состояние ремонта;
3. Состояние профилактики.
Интенсивность – величина, обратная соответствующему времени.
Порядок решения:
1) Анализ состояний;
2) Анализ переходов с указанием интенсивности соответствующих событий.
Рассмотрим вопрос о том, как связана вероятность в момент времени 
и 
.
, 
.
Выражение вероятности 
.
Предположим, что к моменту времени соответствующее исходное состояние (со звездой):
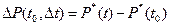(3.1)
Разлагая в ряд (или дифференциал 
) легко можно увидеть, что:
при (типа выходная величина).
Где 
- интенсивность.
рассуждая аналогично для дуги с интенсивностью 
получим, что
или
(3.2)
Уравнение (3.2) называется уравнением Колмогорова-Чепмена.
Если проанализировать эту систему, например, для установившегося режима.
Статика – установившееся состояние.
Определитель этой системы равен нулю.
Из системы одно уравнение убирается, т.к. они линейно-зависимы (одно из уравнений может быть получены из двух других) и заменить его на .
После этого можно получить установившееся значение вероятности 
и можно получить изменение вероятностей в динамике при заданных начальных условиях.
Пример 3.
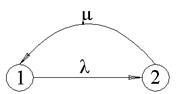
1 – Работоспособная система;
2 – Отказ системы.
Рассмотрим изменение состояний в динамике.
Можно записать по Лапласу.
, 
- начальные условия.
Итак, по Лапласу:
получается система алгебраических выражений:
где 
- коэффициент готовности.
при 
.
Рис. 9. Функция готовности
Рис. 10 Вероятность выхода из строя прибора.
Рис. 11. Вероятность безотказной работы.
