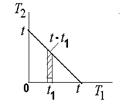
По определению функции распределения системы случайных
величин:
Так как случайные величины T 1 и T 2 независимы, функция
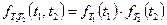распределения их системы:
- 
композиция законов распределения случайных
времён эксплуатации и есть функция распределения
потока отказов.
Так как в результате замены или ремонта получаем элемент с идентичными свойствами:
С использованием обозначений, принятых в теории надёжности получим:
 | |||
 | |||
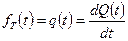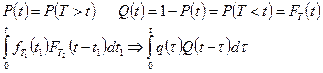выражение закона распределения при двух отказах
 |
Среднее число отказов за время t:
7. В случае эксплуатации элемента с заменами при пренебрежимо малом времени его восстановления как определить наименьшее число запасных элементов, обеспечивающих нормальную эксплуатации Вашей установки?
Примем, что поток отказов элемента является простейшим потоком, т. е. потоком Пуассона. Вероятность того, что за время t произойдет ровно k отказов 
(3.1)
Вероятность того, что за время t число отказов превысит n, будет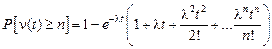 
. (3.2)
При большом значении n ряд, входящий в (3.2), может быть при использовании центральной предельной теоремы Ляпунова просуммирован: 
, (3.3)
где 
– функция (интеграл) Лапласа;
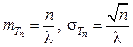– математическое ожидание и среднеквадратическое отклонение времени наступления n -го отказа (Тn.).
